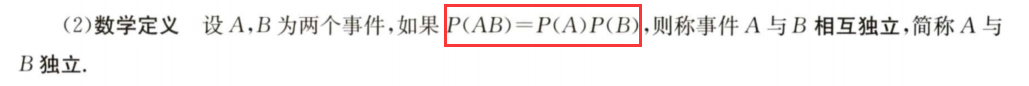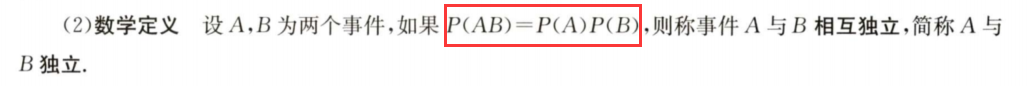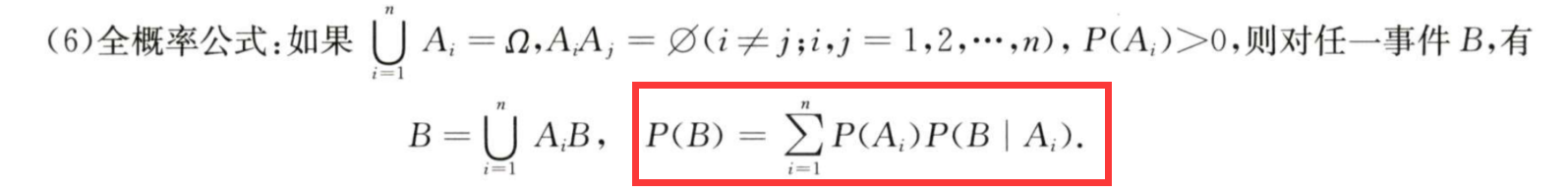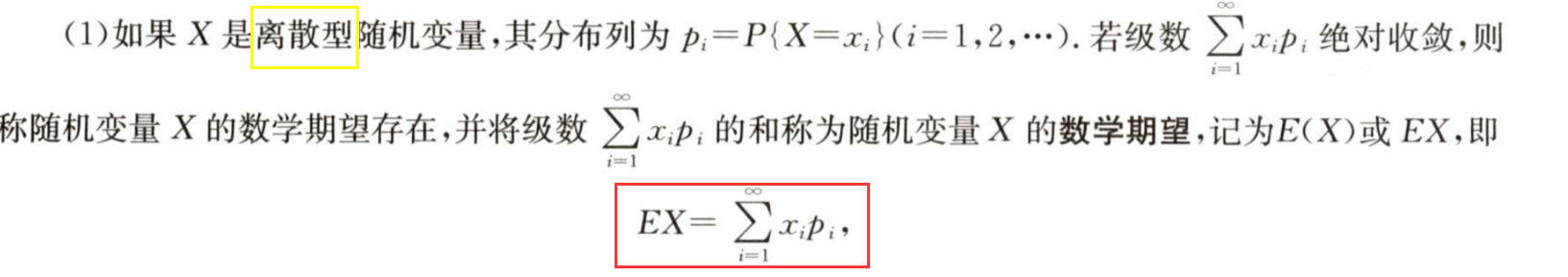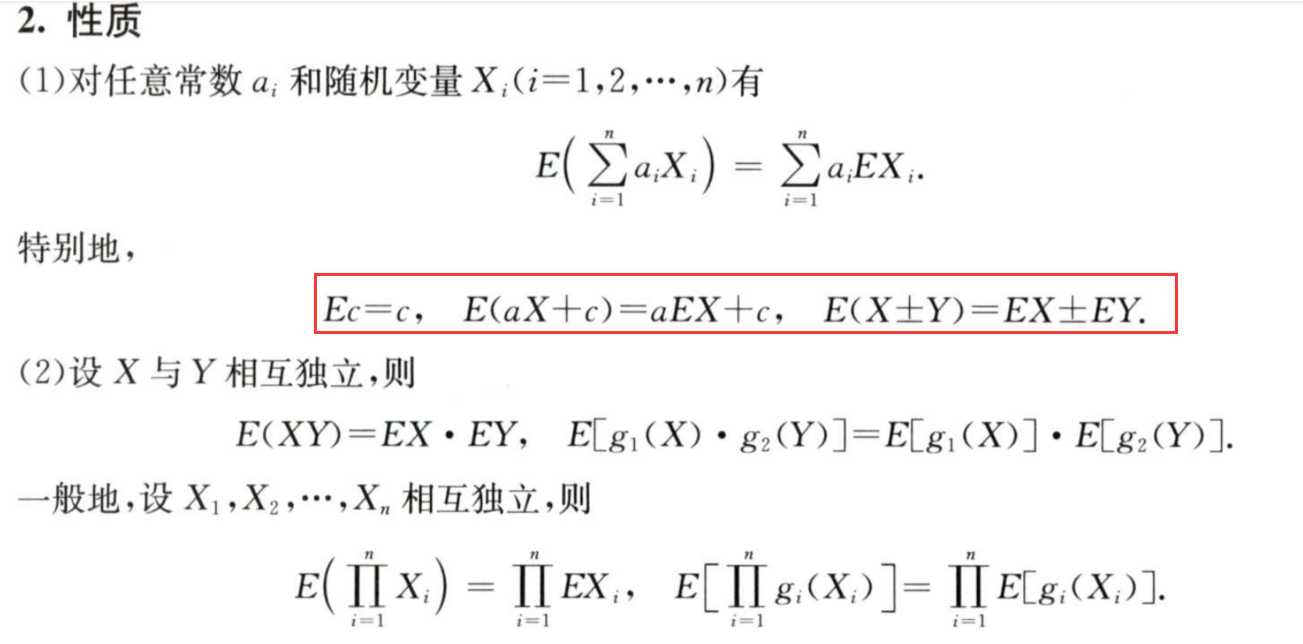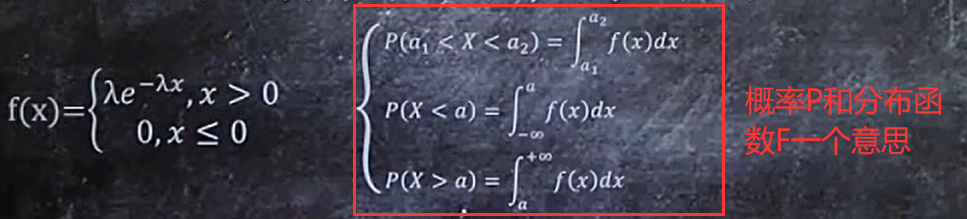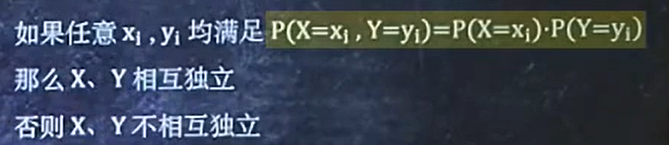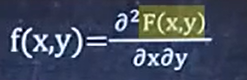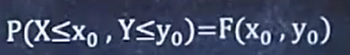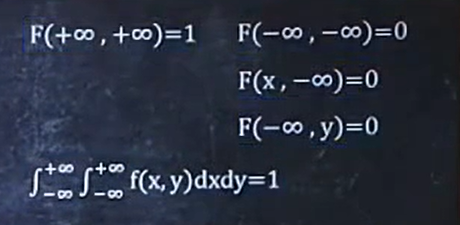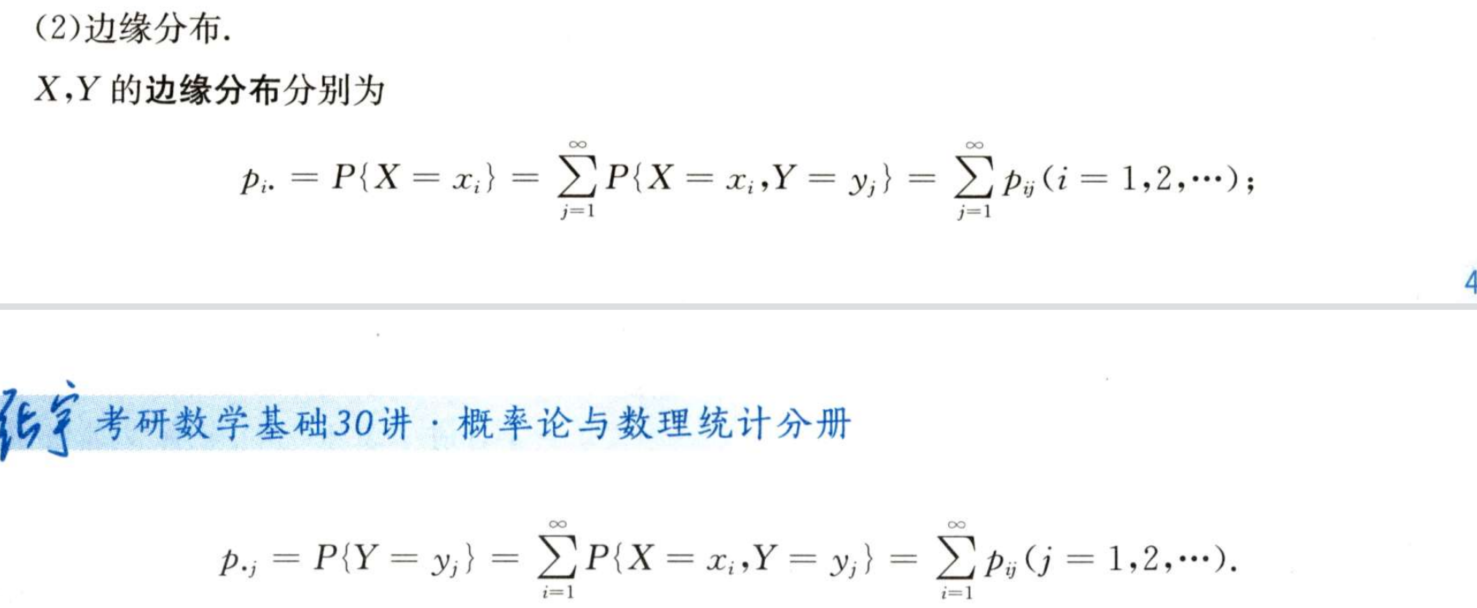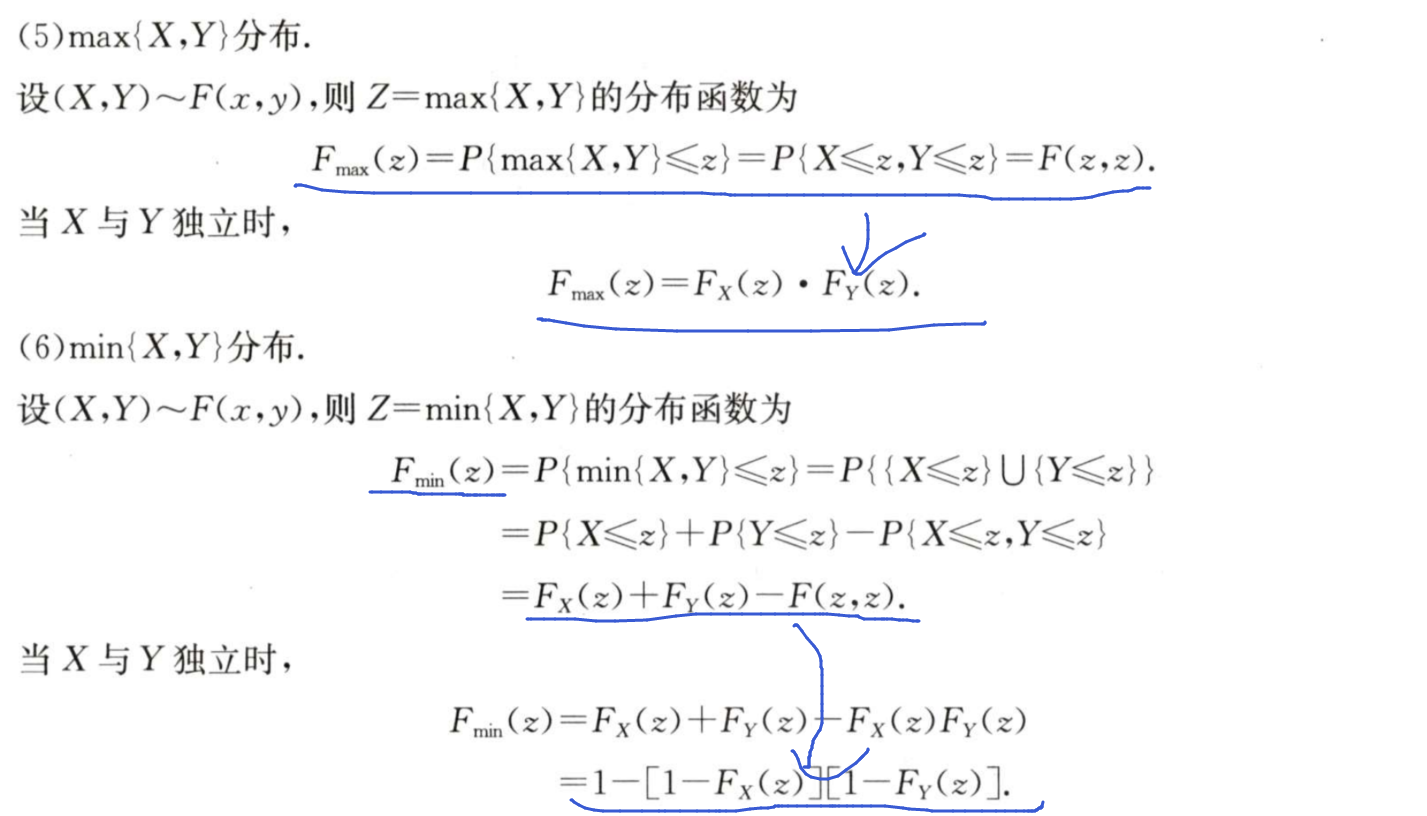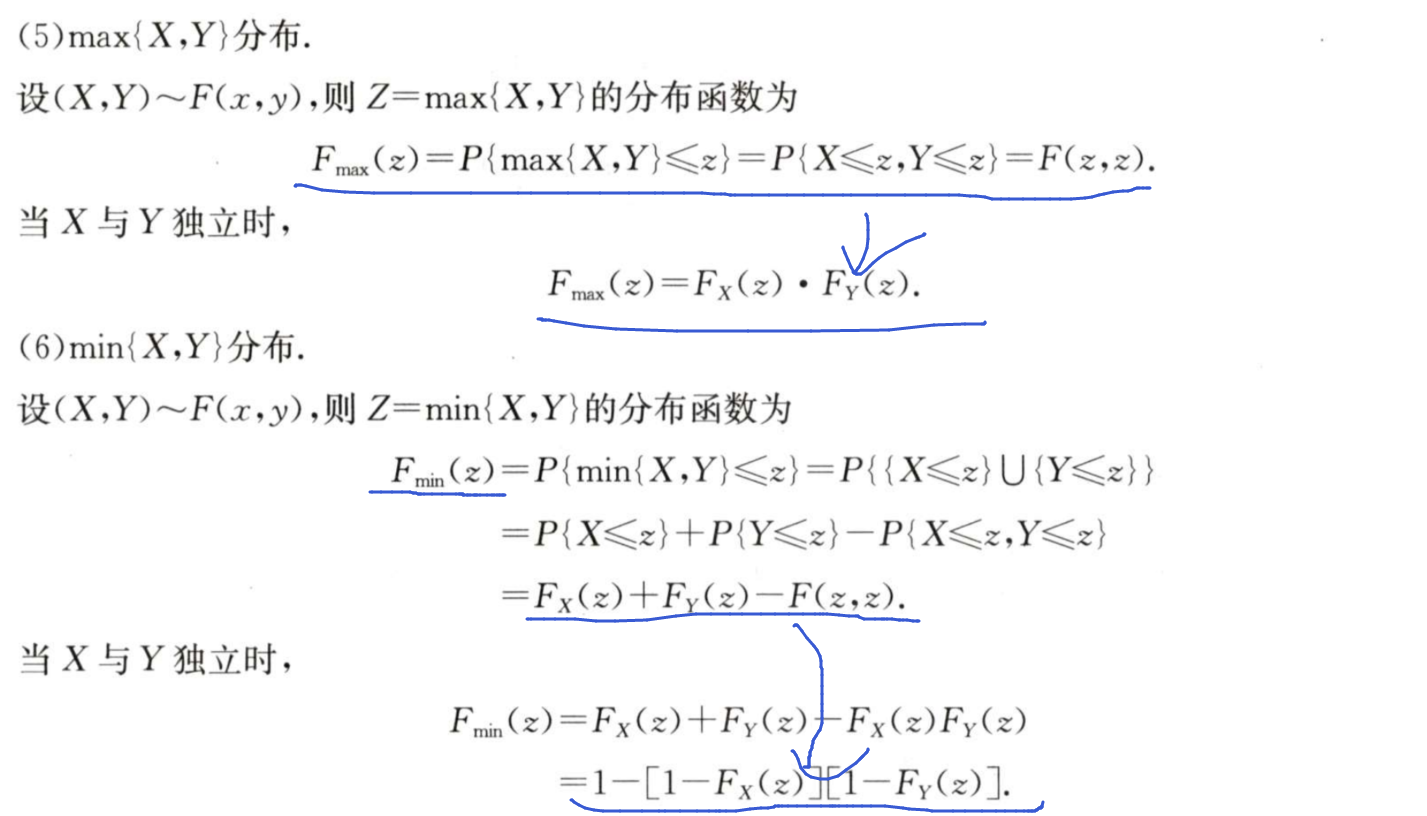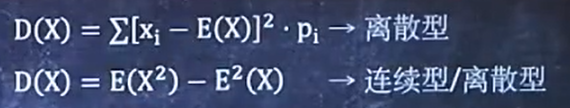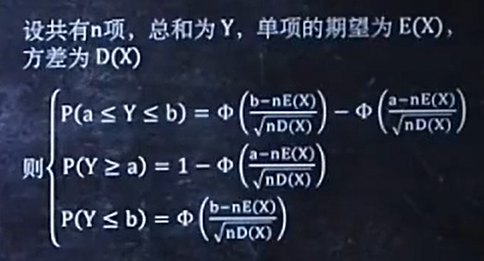重点章节
条件概率,期望等等
第一课 随机事件和概率
1/6 无放回类题目(一次摸多个)
例 1. 盒子里有 3 绿 4 红共 7 个小球,无放回的摸 3 个试求摸出 1 绿 2 红的概率 例 2. 钱包里有 3 张 100 元, 5 张 10 元, 3 张 5 元的纸币,随机摸 3 张,试求摸出 1 张 100 , 2 张 10 的概率 例1.盒子里有3绿4红共7个小球,无放回的摸3个试求摸出1绿2红的概率\\ 例2.钱包里有3张100元,5张10元, 3张5元的纸币,随机摸3张,试求摸出1张100,2张10的概率 例1.盒子里有3绿4红共7个小球,无放回的摸3个试求摸出1绿2红的概率例2.钱包里有3张100元,5张10元,3张5元的纸币,随机摸3张,试求摸出1张100,2张10的概率
【无放回,直接用C解】
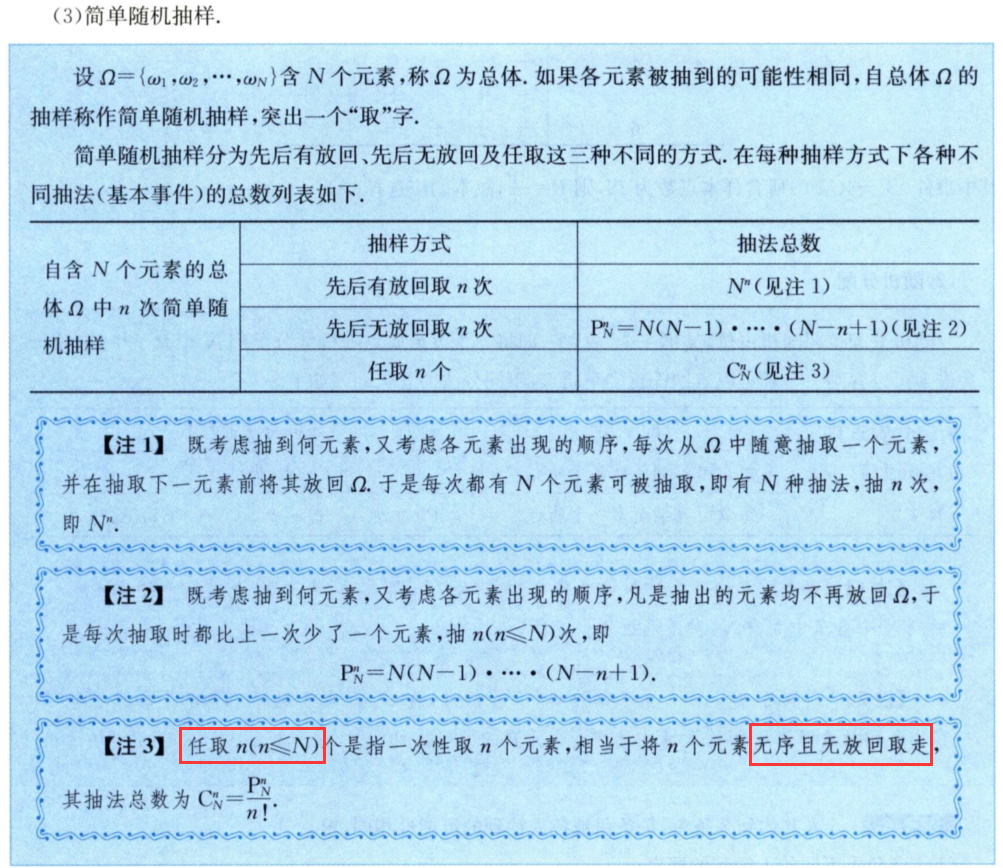
古典概型

排列与组合
2/6 有放回题目(进行多次,每次情况一致)

3/6 事件的概率

4/6 条件概率
①条件概率
②相互独立

法二:
P
(
A
‾
∣
B
)
=
1
−
P
(
A
∣
B
)
=
1
−
P
(
A
B
)
P
(
B
)
由于
A
B
相互独立,所以
P
(
A
B
)
=
P
(
A
)
P
(
B
)
P
(
A
‾
∣
B
)
=
1
−
P
(
A
∣
B
)
=
1
−
P
(
A
)
P
(
B
)
P
(
B
)
=
0.6
P(\overline A|B)= 1-P(A|B)=1-\frac{P(AB)}{P(B)}\\ 由于AB相互独立,所以P(AB)=P(A)P(B)\\ P(\overline A|B)= 1-P(A|B)=1-\frac{P(A)P(B)}{P(B)}=0.6\\
P(A∣B)=1−P(A∣B)=1−P(B)P(AB)由于AB相互独立,所以P(AB)=P(A)P(B)P(A∣B)=1−P(A∣B)=1−P(B)P(A)P(B)=0.6
5/6 全概率公式

6/6 贝叶斯公式
贝叶斯其实是条件概率反过来求。其实就是**已知结果求原因**

第二课 离散型随机变量
1/6 求分布律里的未知数
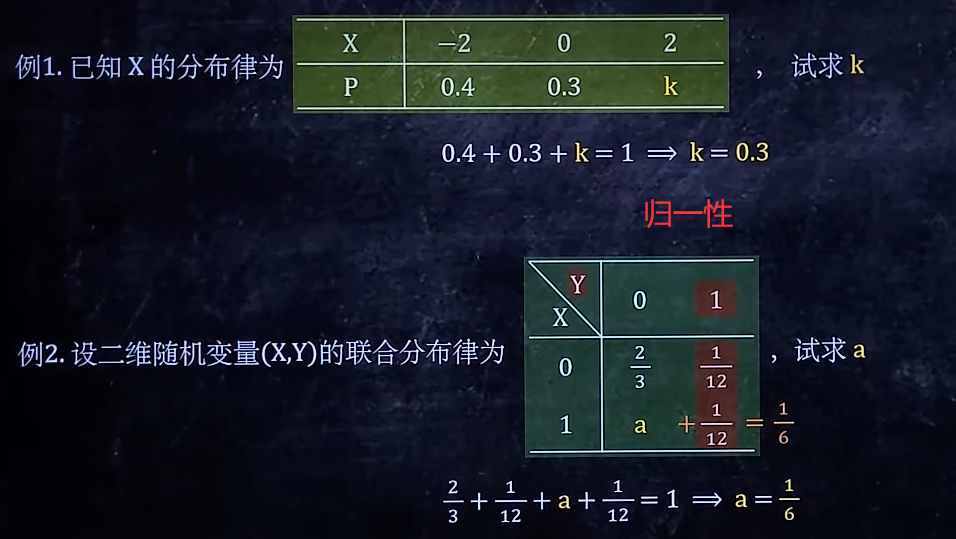
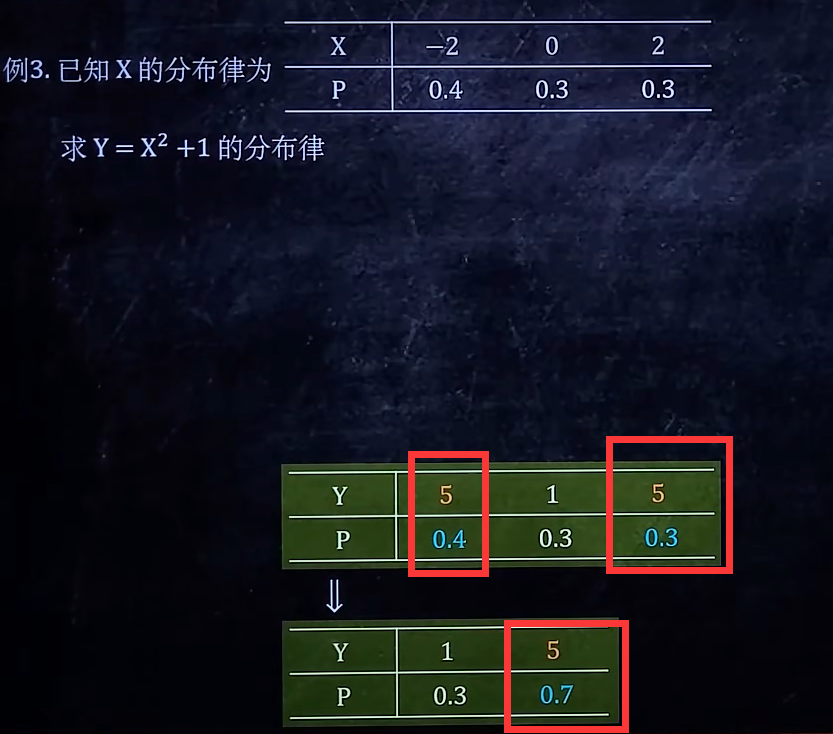
2/6 根据X的分布律写Y的分布律
一维随机变量函数的分布
注意
3/6 根据(X,Y) 的分布律写Z的分布律
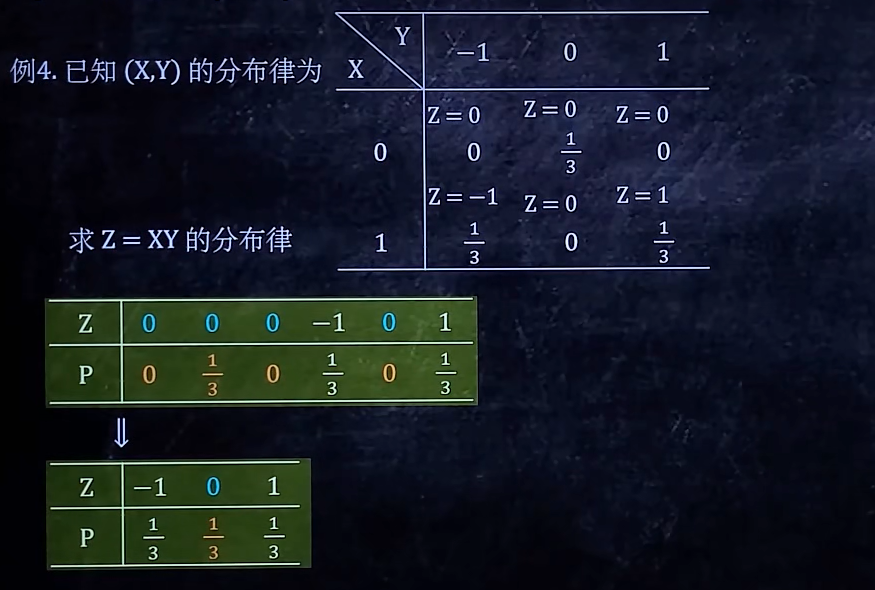
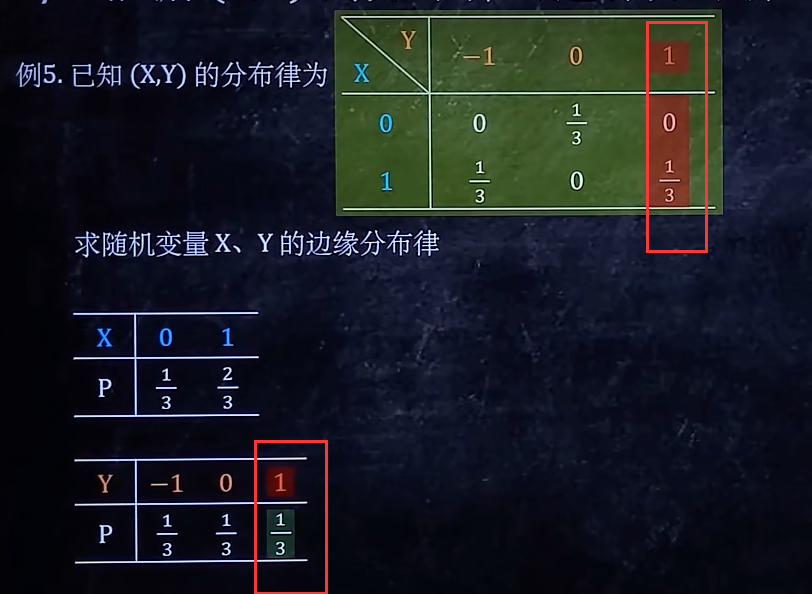
4/6 根据(X,Y)的分布律写边缘分布律
边缘分布
5/6 X与Y相互独立时的联合分布律

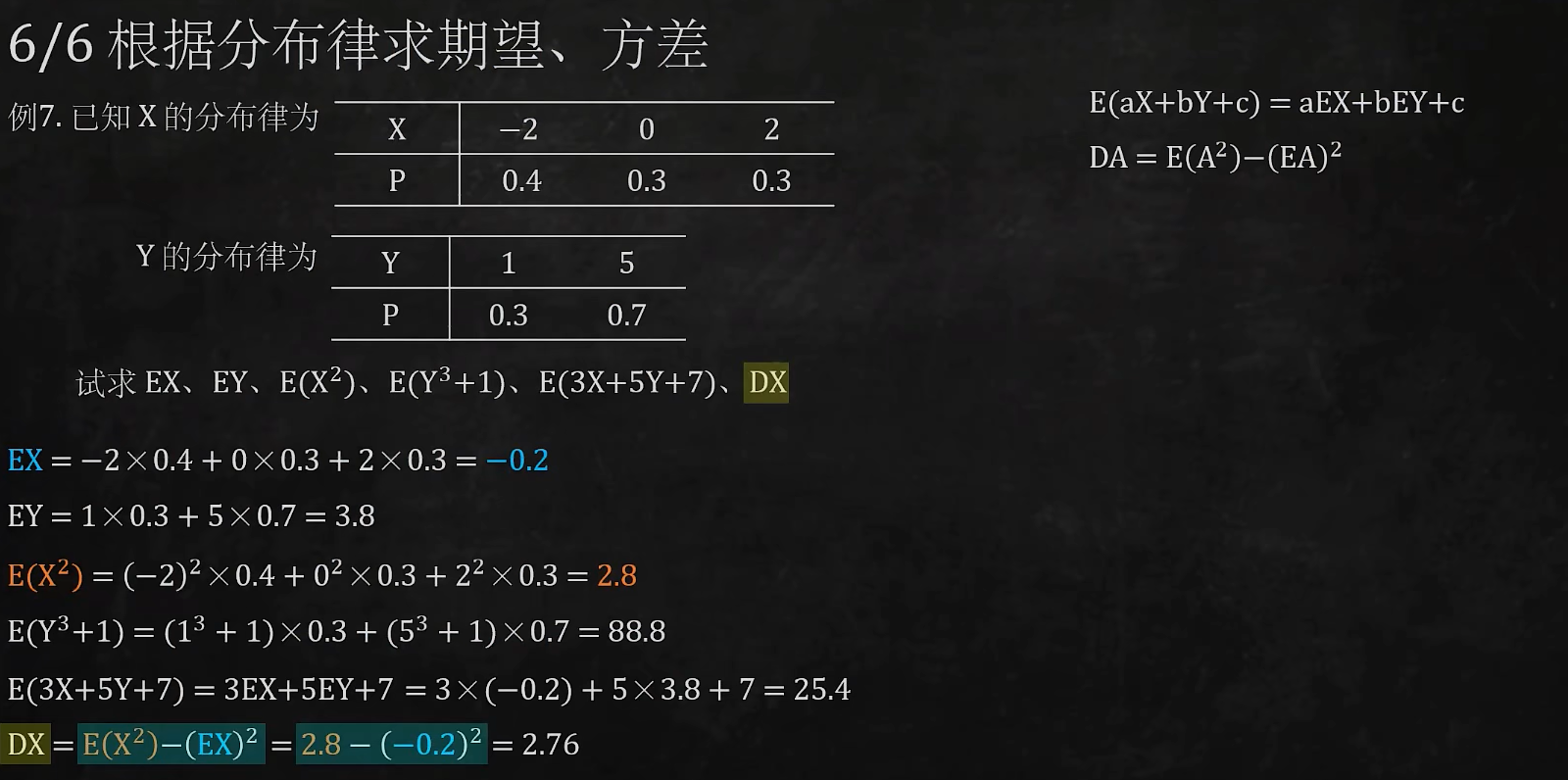
6/6 根据分布律求期望、方差
①离散型随机变量的数学期望
②离散型随机变量的方差
③一维随机变量函数的分布
第三课 连续型需要的积分
1/4 求分段函数在确定区闻的定积分

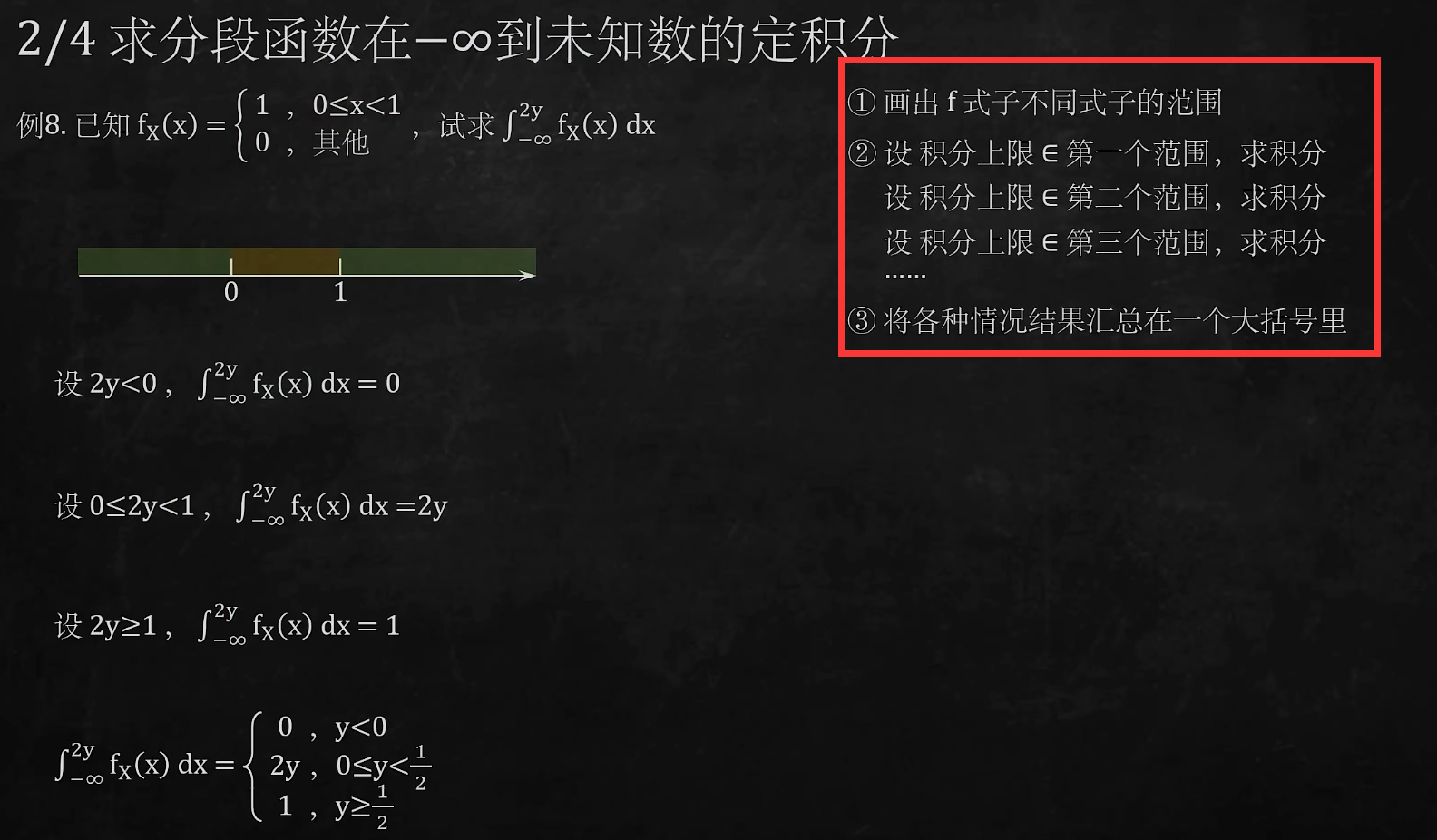
2/4 求分段函数在-∞到未知数的定积分
3/4 求简单的二重积分

4/4 求f(x,y)的二重积分

第四课 一维连续型随机变量
1/7 已知fx(x)求概率
P=F,F是对应概率密度函数f上的积分
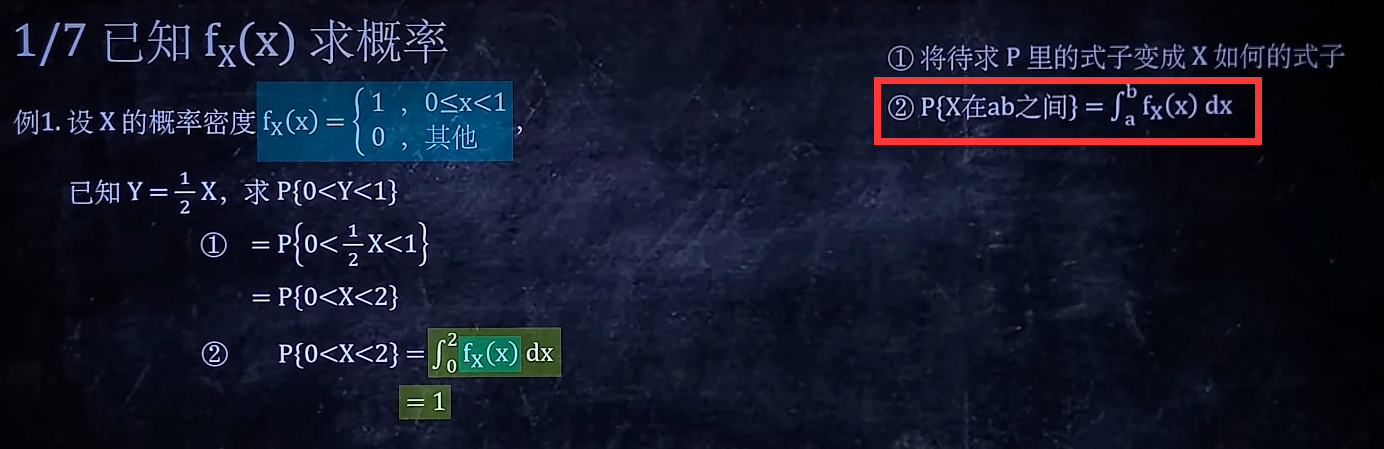

2/7 求fx(x) 中的未知数
归一性
【取遍-∞到+∞】
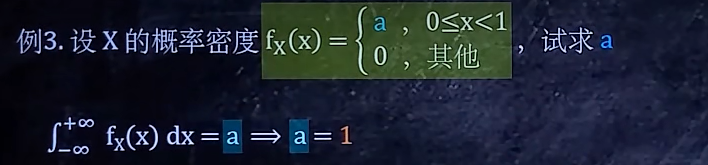
3/7 已知f(x)求F
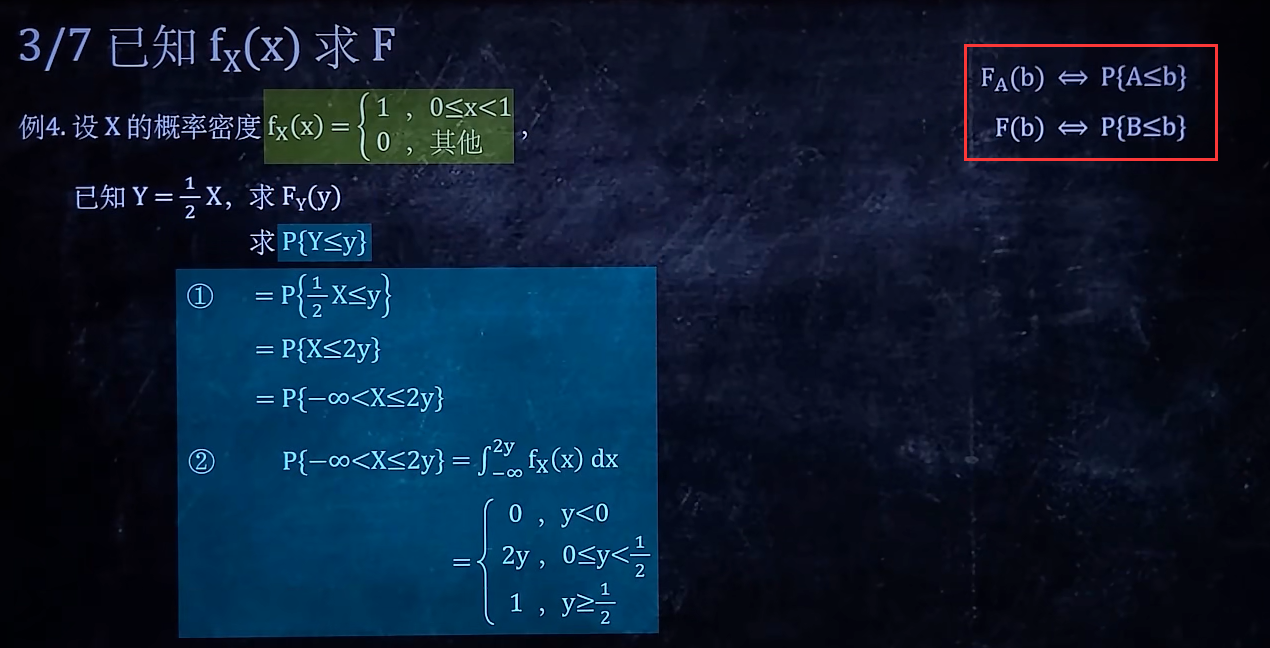
4/7 求F中的未知数

由于分布函数F是右连续函数,所以条件三成立
5/7 已知F求f
分布函数的反求

6/7 已知f求f
①连续型–>连续型(混合型)
②例题


7/7 已知f求期望、方差
①X的数学期望
②方差

4.常见的五种分布
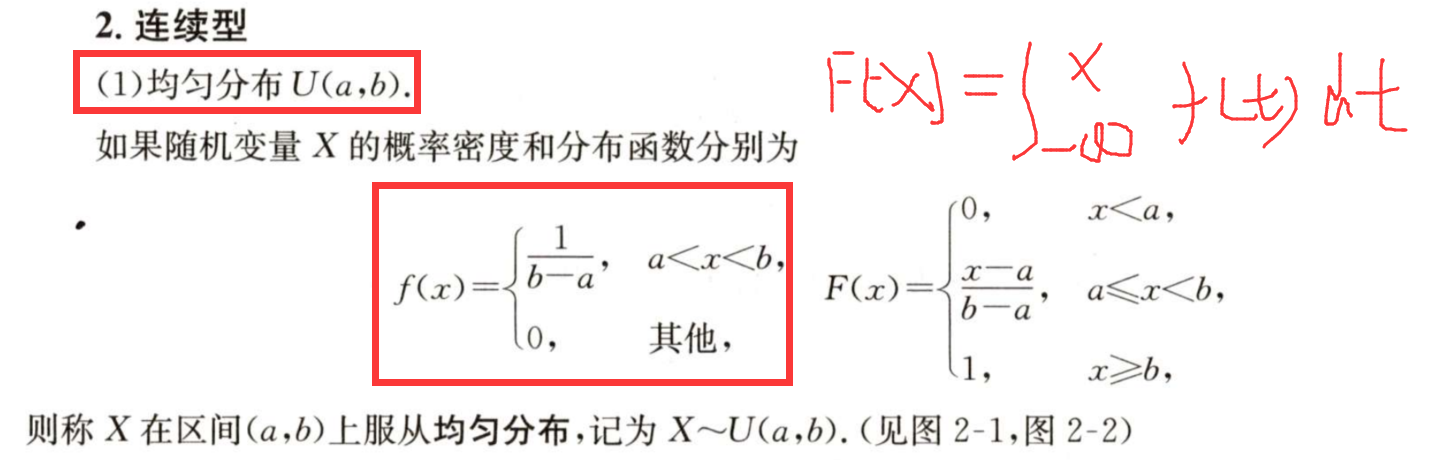
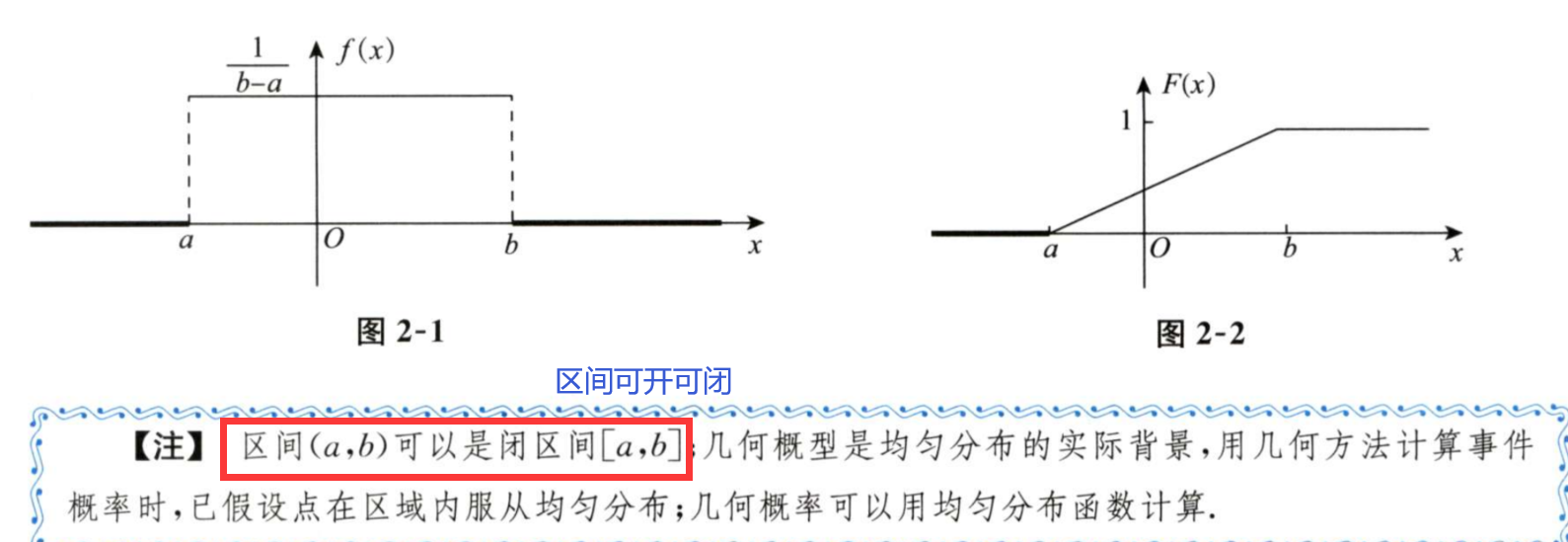
1/6 符合均匀分布,求概率
均匀分布U(a,b)

2/6 符合泊松分布,求概率
泊松分布P(A)
【lambda是参数,x是某某次数】

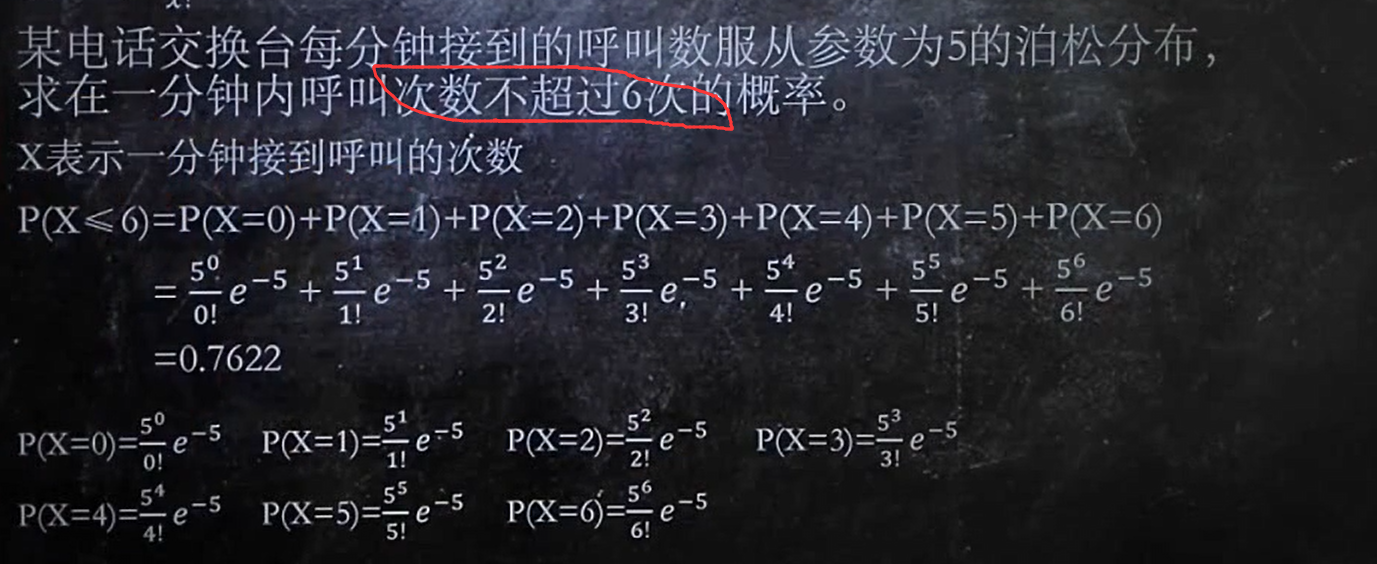
如果是这样的,千万不要用1-P(X=6)这种,要一个一个算!
3/6符合二项分布,求概率

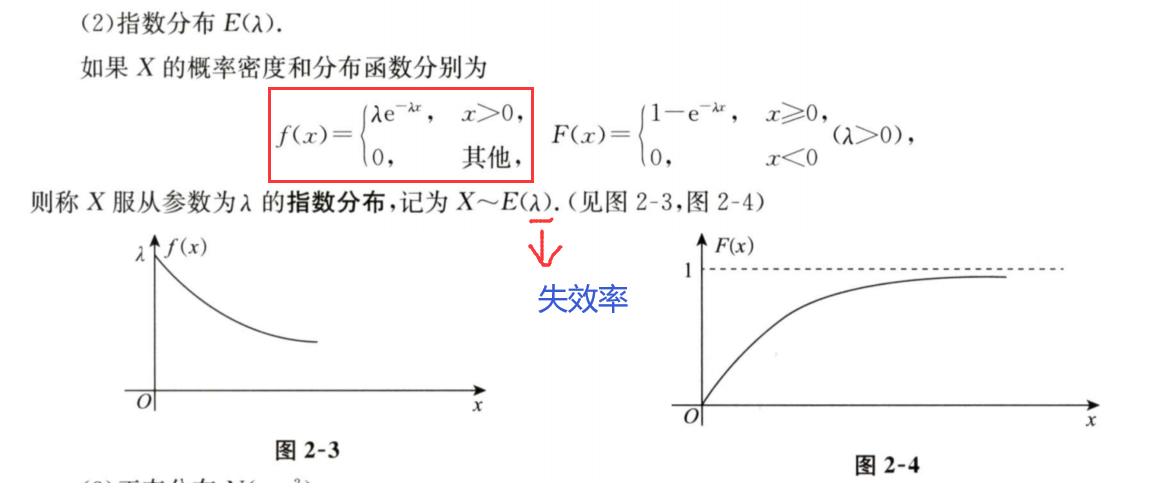
4/6 符合指数分布,求概率

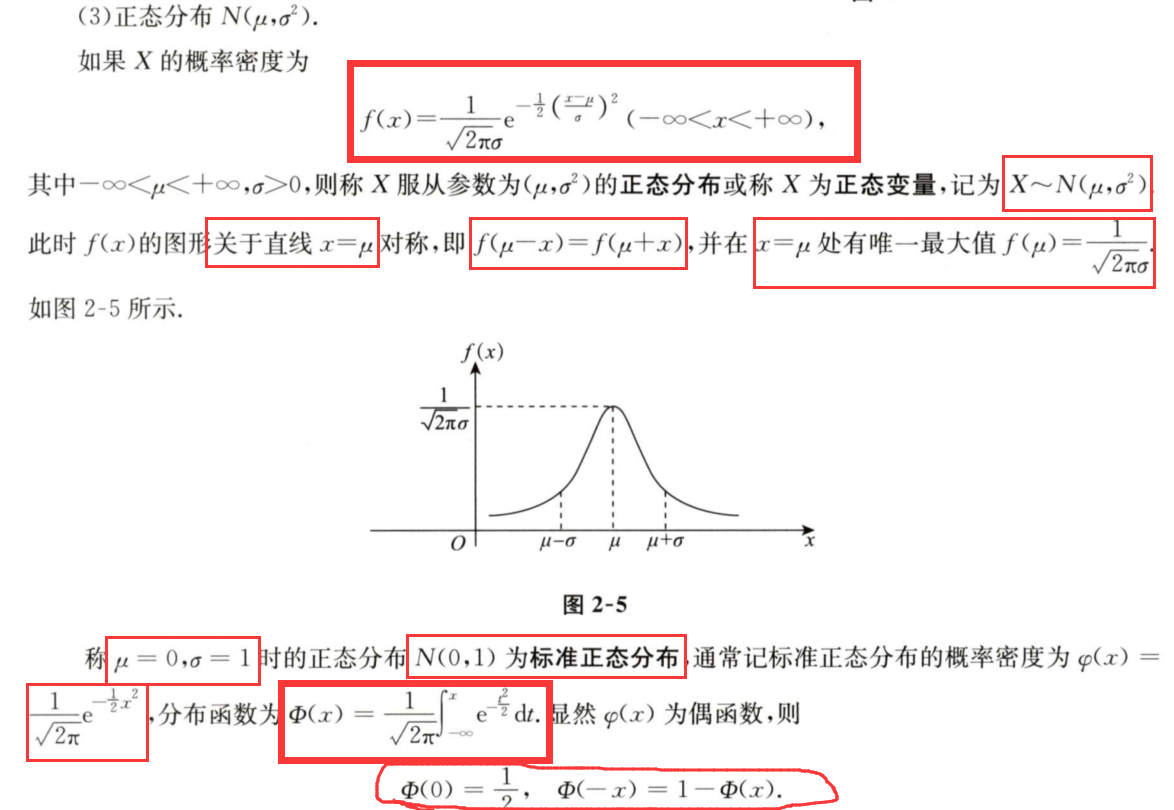
5/6 符合正态分布,求概率
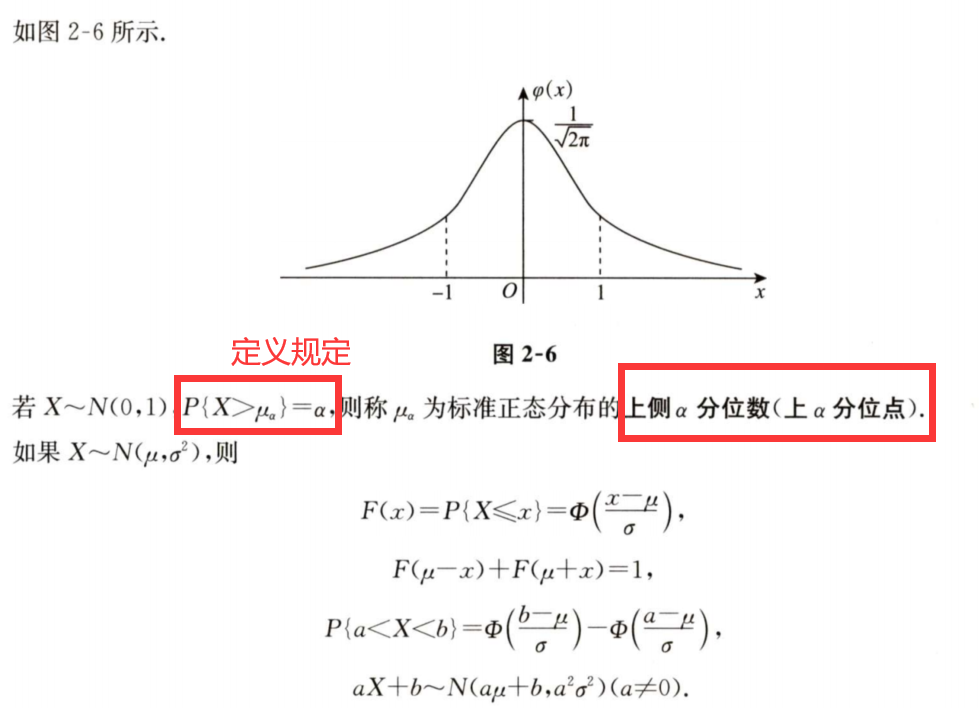
正态分布

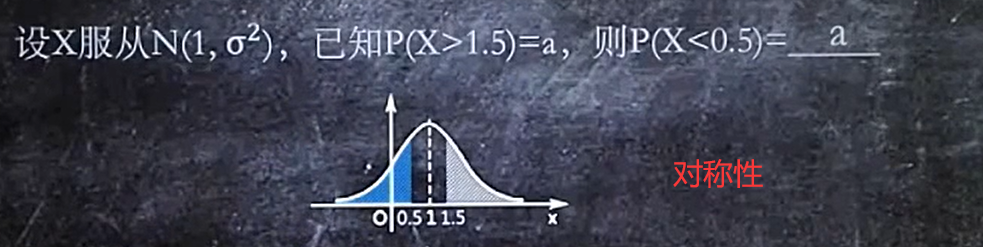
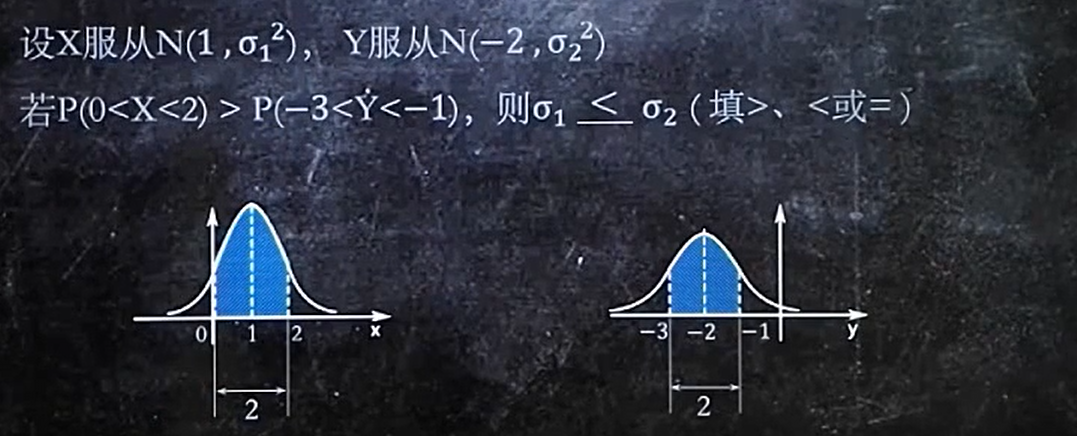
6/6 正态分布图像
1.面积表示概率,整个正态分布图像的总面积为1
2.图像关于u对称
3.o越小,图像越陡 【标准差o】
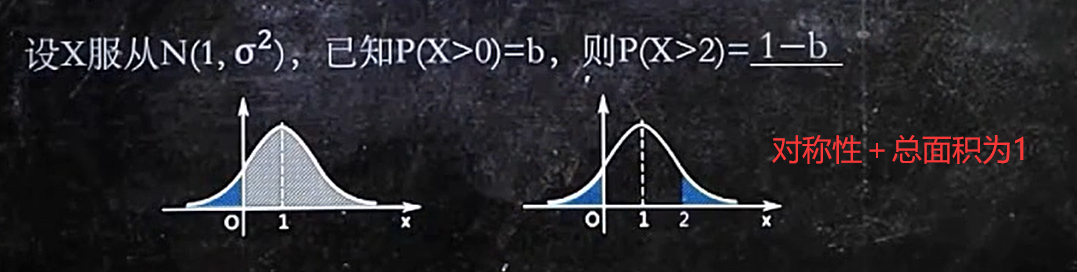
5.离散型二维变量与连续性二维变量(上)
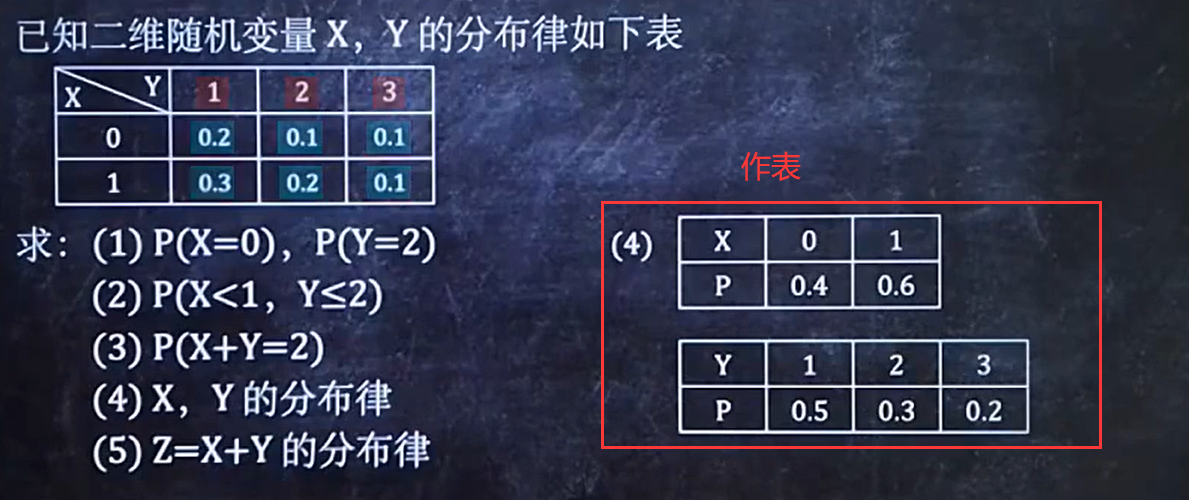
1/8 已知二维离散型分布律,求???
离散型直接看表
【做题方法参考如下】

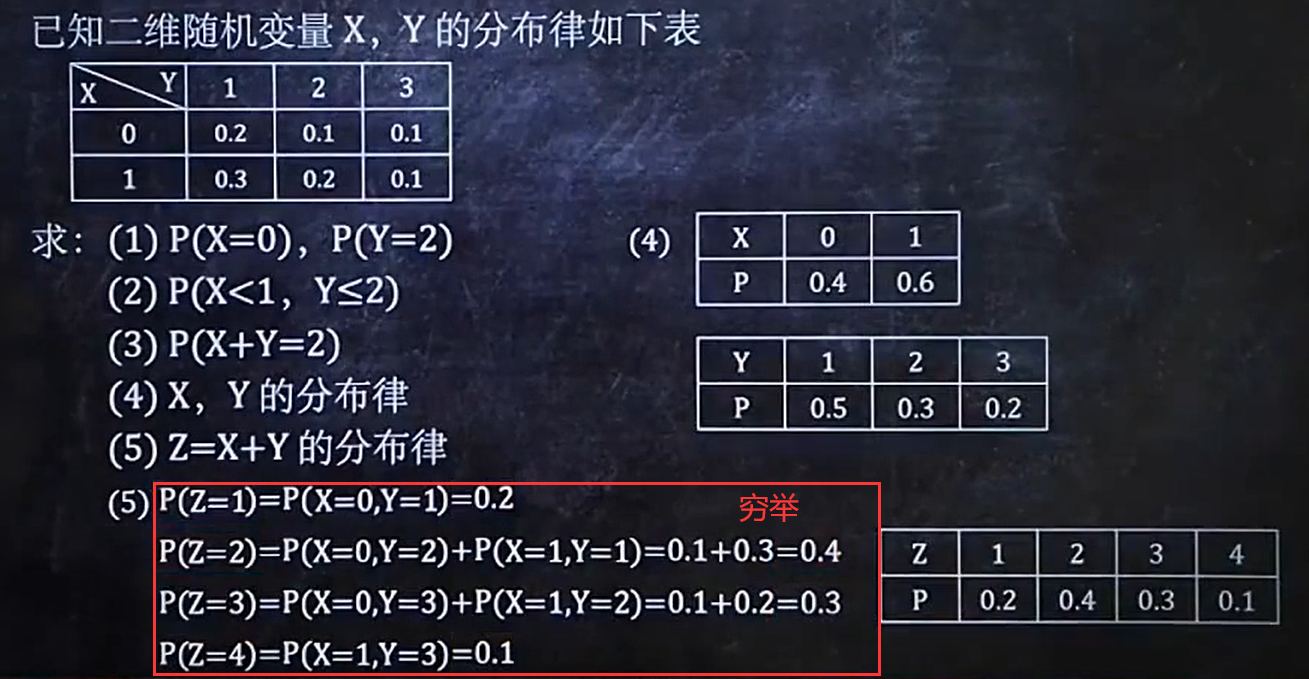
2/8 已知二维离散型分布律,判断独立性
如果满足p(xy) = p(x) * p(y),那么相互独立
则我们只需要验证每一个p(xy) = p(x) * p(y),就可以验证独立性
例1:

例2:

3/8 已知F(x,y)求f(x,y)
F(x,y)是联合分布函数
f(x,y)是联合概率密度
例1:

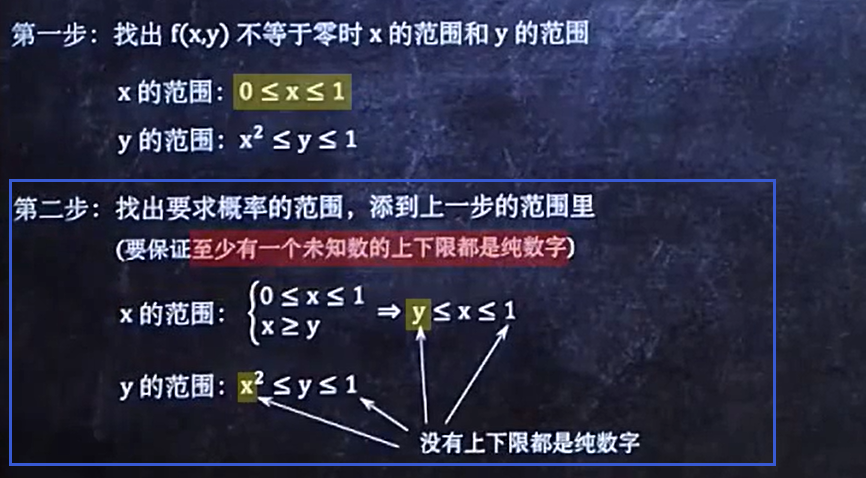
4/8 已知f(x,y)求F(x,y)
- 找出f(x,y)不等于0时x的范围和y的范围
- 计算结果
- 带入计算
- 区域
二维连续型随机变量的概率密度
做题步骤


5/8 已知F(x,y)求P
记住公式然后带入
例一:

例二:

6/8 已知f(x,y)求P
注意解题步骤,求范围再带入求更细的范围【进一步缩小求值范围】,再带入二重积分中
例一:
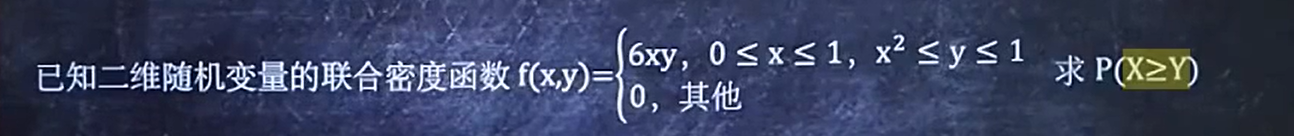

例二:
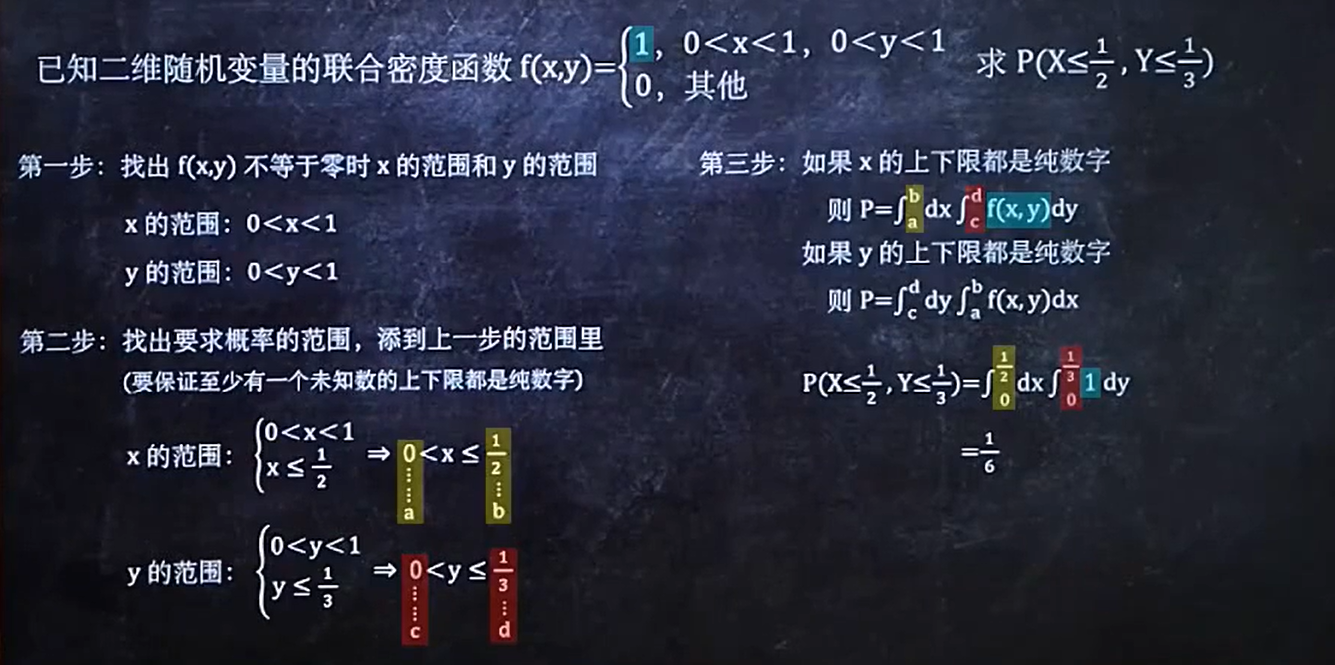
7/8求F(x,y)或f(x,y)中含有的未知数
记住下面的式子

8/8 求均匀分布的f(x,y)与P
记住下面的式子

6.连续型二维变量(下)
1/7 求边缘分布函数
边缘概率密度
边缘概率密度

2/7 求边缘密度函数
边缘概率密度

3/7 判断连续型二维变量的独立性
F(x,y) = Fx(X) * Fy(Y)那么X、Y互相独立
f(x,y) = fx(X) * fy(Y)那么X、Y互相独立
这种题目带入验证就可以了
先求出 fx(X) 和 fy(Y)带入计算验证就OK了
如何求出 fx(X) 和 fy(Y)在上一个题型说了

4/7 已知f(x,y),Z=X+Y,求fz(Z)
(卷积公式)
利用公式进行分类讨论就好啦

5/7 已知f(x,y),Z=x/y,求fz(Z)
同理4/7

6/7 已知f(x,y),且X,Y相互独立,Z=max(X,Y),求Fz(Z)
记住一个公式:Fz(Z) = Fx(Z)*Fy(Z)
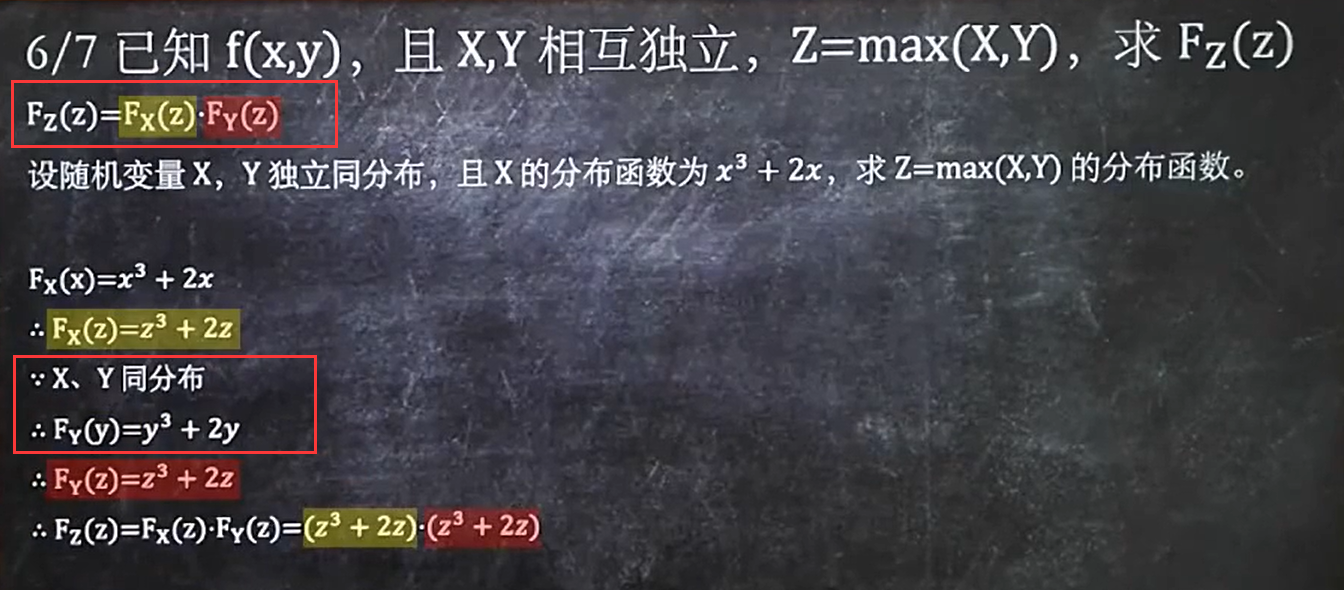
7/7 已知f(x,y),且X,Y相互独立,Z=min(X,Y),求Fz(Z)
同上面6/7的题目的公式不一样:Fz(Z)=1-[1-Fx(Z)]*[1-Fy(Z)]
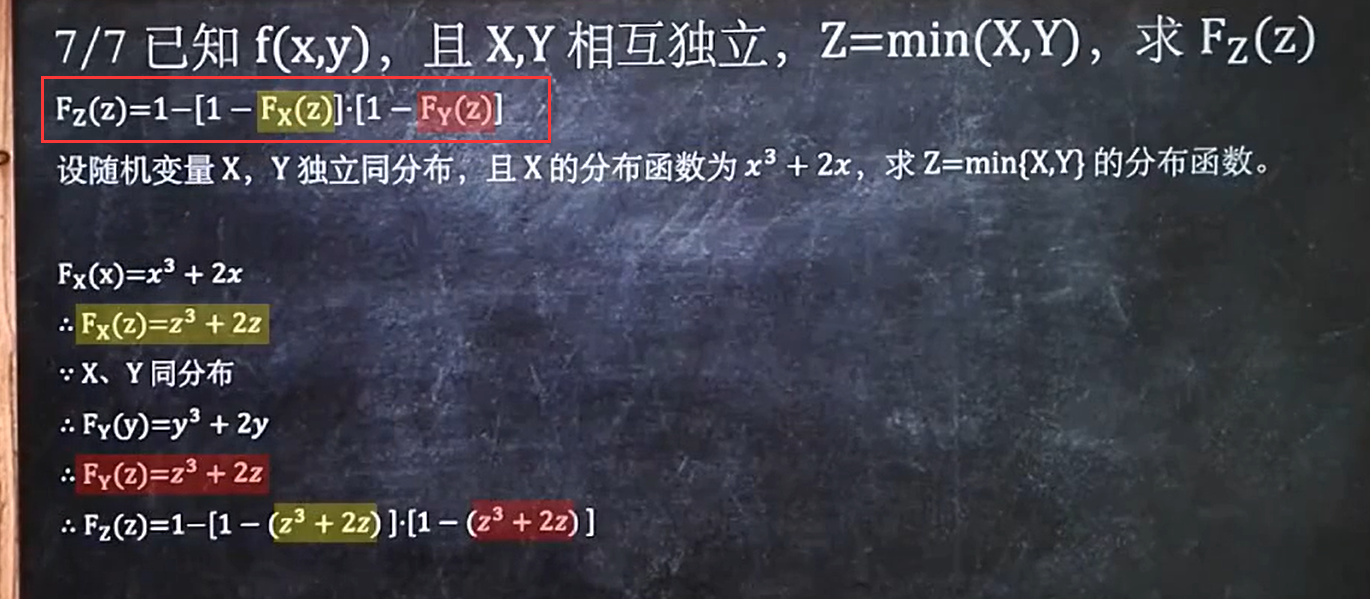
7.随机变量的数字特征(上)
1/6 求离散型的期望E(X)
离散型随机变量的期望

2/6 求连续型的期望E(X)
连续型随机变量的期望

3/6 已知Y=g(x),求E(Y)
连续型随机变量函数的期望
例题1(离散型):

例题2(连续型):

4/6 求方差D(X)
记住两个公式(主要是第二个D(x)=E(x2)-[E(x)2]
例题1(离散型):

例题2(连续型):
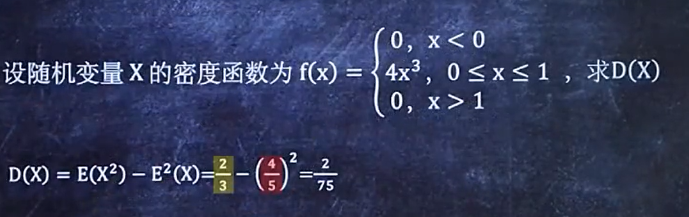
5/6 根据E(x)、D(x)的性质进行复杂运算
例题:
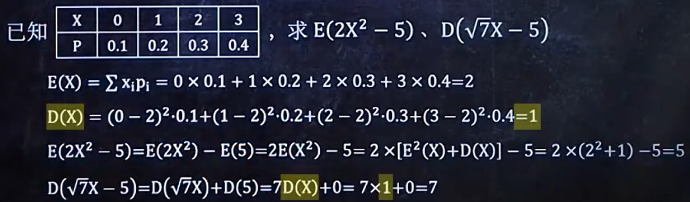
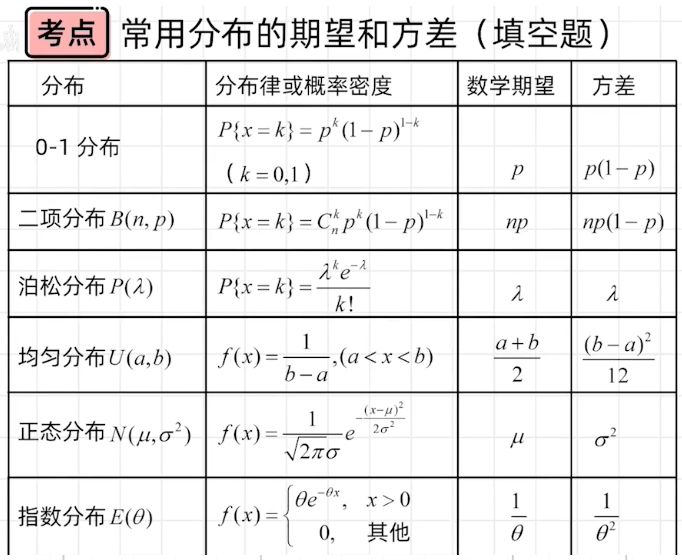
6/6 E(x)、D(x)与各种分布的综合题
各种分布的公式:
例题1:(二项分布)
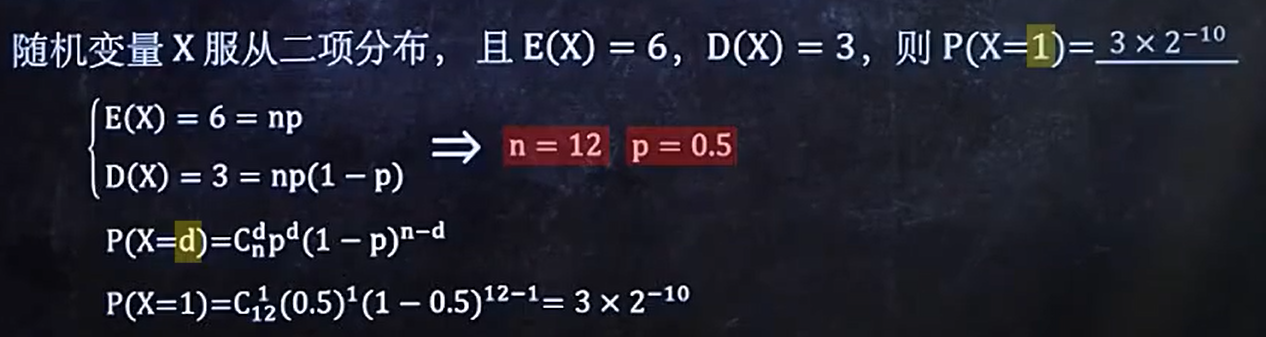
例题2:(泊松分布)

8.随机变量的数字特征(下)与中心极限定理
1/3 Cov、ρxy、D相关类题目
两个随机变量的协方差与相关系数
例题1:
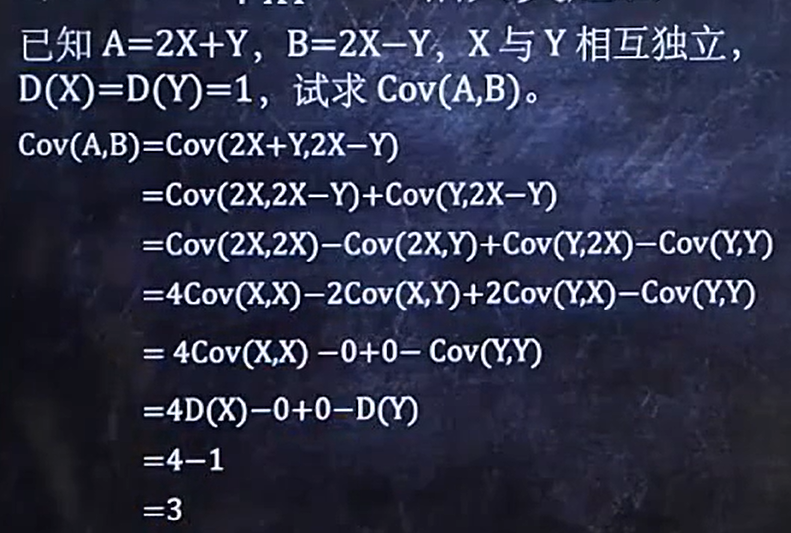
例题2:
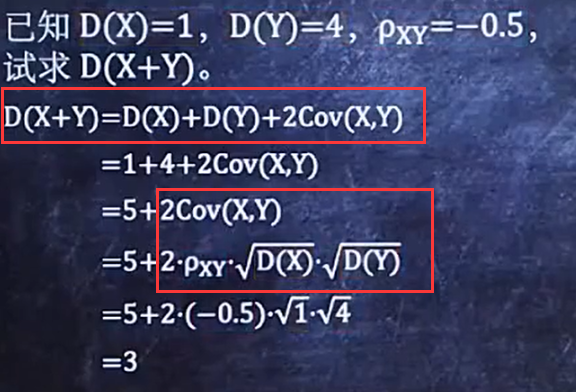
2/3 利用切比雪夫不等式求概率
切比雪夫不等式
例题:

3/3 多项独立同分布,求总和怎样的概率
还是看公式:
例题1:

例题2:
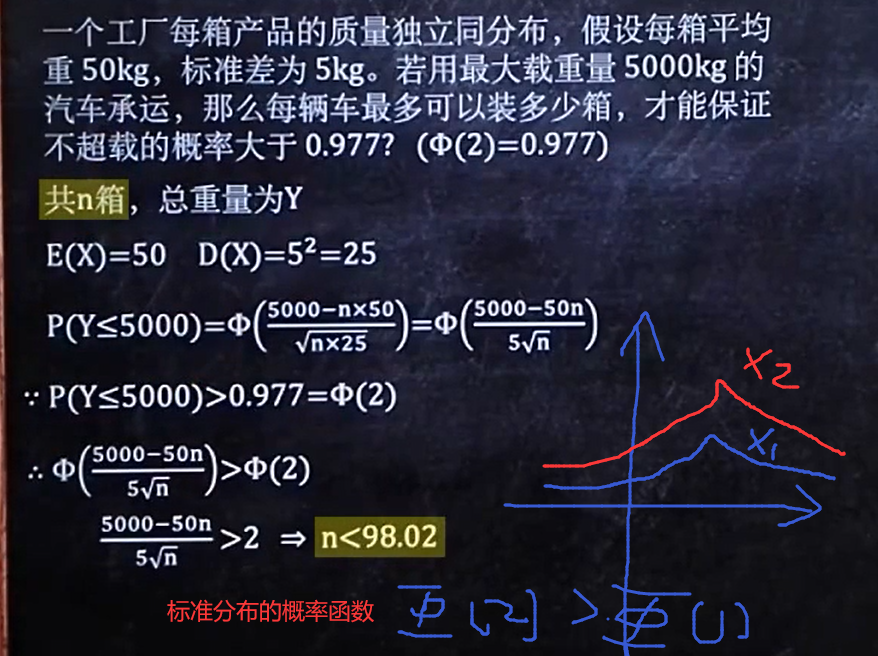
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-smWwgpWk-1673279625538)(C:\Users\23972\AppData\Roaming\Typora\typora-user-images\image-20230107160630898.png)]](https://img-blog.csdnimg.cn/144d7f947c834beaa4fb5f58c43a0630.png)