【NBUOJ刷题笔记】递推_递归+分治策略2

news2025/1/13 10:36:45

0. 前言

PS：本人并不是集训队的成员，因此代码写的烂轻点喷。。。本专题一方面是巩固自己的算法知识，另一方面是给NBU学弟学妹们参考解题思路（切勿直接搬运抄袭提交作业！！！）最后，该系列博客AC代码均以Java语言提交，C/C++的可以参考思路编写代码

1. 题目详情

1.1 题目一：第K小的数

1.1.1 题目信息

题目描述：
输入n个数，求其中第k小的数。（要求采用分治法完成，不建议采用完整的排序）
输入要求：
第一行包含两个整数n和k；n<1000，1<=K<=n
第二行包含n个整数。
输出要求：
输出第k小的那个整数_。_
输入样例：
15 1
1 3 7 2 4 6 -1 0 9 88 2 5 17 6 1
输出样例：
-1
来源：
NBUOJ

1.1.2 算法思路（分治法）

本题的一般思路有如下几种：

  • 借助堆/优先级队列实现的TopK问题
  • 基于完整的排序算法
  • 分治策略

由于题目限制使用分治思想，因此这里介绍最后一种方法
分治思想：简单来说就是分而治之，化繁为简，将大问题分解成子问题逐一求解
算法步骤（重要）：

  1. 题目要求找到n个数中第k小的元素，我们首先在当前数组中随意选中一个基准元素pivot
  2. 然后使用双指针 区域划分 的思想将数组划分为两部分，其中左半区域的元素比pivot小，右半区域的元素比pivot大
  3. 此时假设pivot基准元素的下标是pivotIndex，pivot元素就是整个数组中第 pivotIndex + 1 小的元素
  4. 此时令左半区域的元素个数为leftNum，如果 k==leftNum + 1 那么直接返回基准元素，如果 k < leftNum + 1 那么就递归左半部分区域继续找到第k小的元素，如果 k > leftNum + 1 ，那么就递归右半部分区域递归找第k - (leftNum + 1)小的元素

PS：如果不清楚数组区域划分算法的小伙伴可以自行搜索或者直接看下面的代码实现部分
示例：我们使用上述给出的测试用例画图讲解：
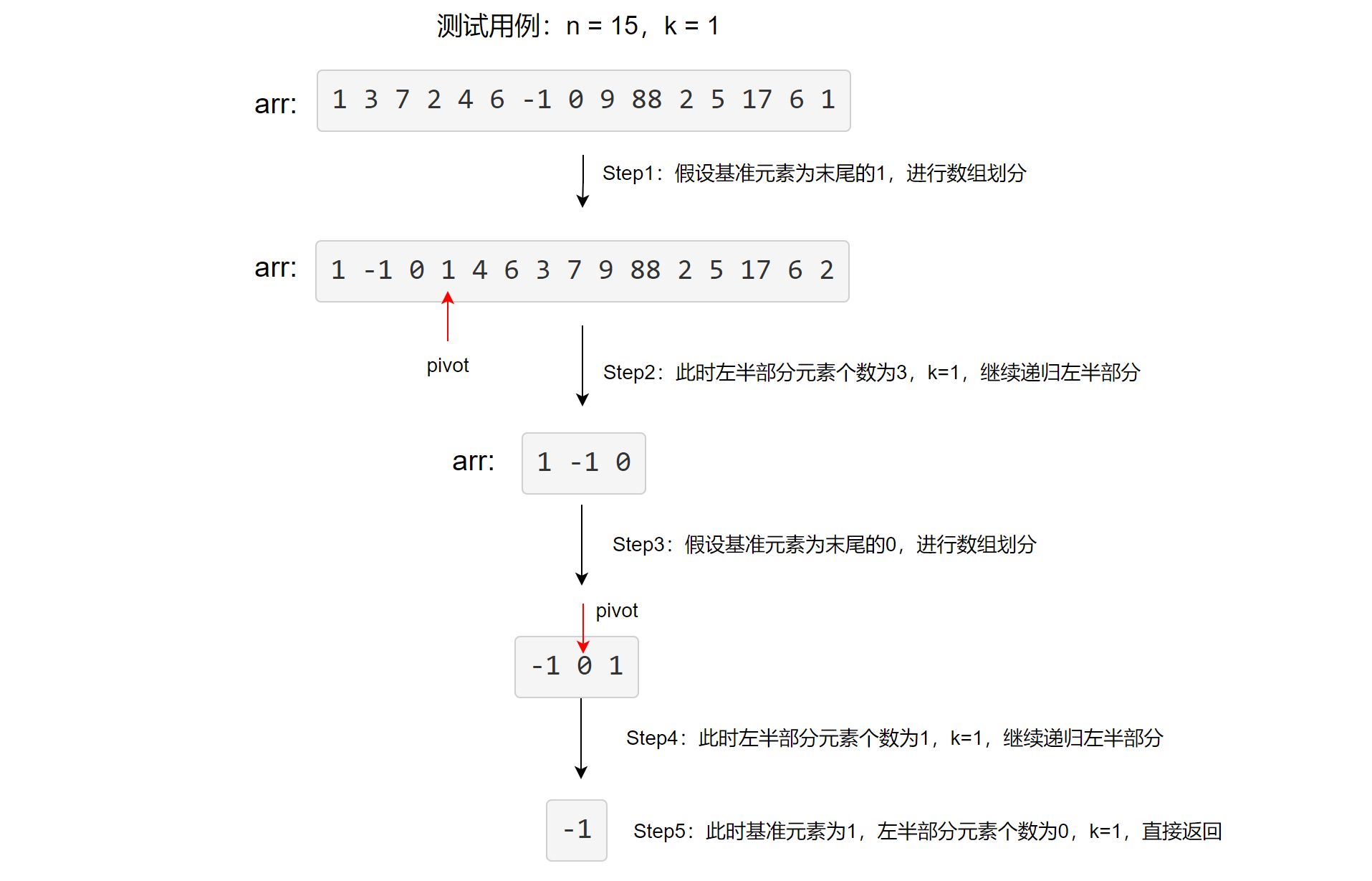
image.png

1.1.2 AC代码（Java实现）

NBUOJ上面Java带中文注释会报错！因此这里放了两个版本的代码，前面不带注释的可以直接跑OJ通过，后面的方便读者阅读

1.1.2.1 不带注释版本
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int k = scanner.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = scanner.nextInt();
        }
        System.out.println(partition(arr, 0, n - 1, k));
    }

    private static int partition(int[] arr, int left, int right, int k) {
        int pivot = arr[right];
        int prev = left - 1; 
        int cur = left;
        while (cur <= right) {
            if (arr[cur] <= pivot) {
                int tmp = arr[prev + 1];
                arr[prev + 1] = arr[cur];
                arr[cur] = tmp;
                cur++;
                prev++;
            } else {
                cur++;
            }
        }
        int leftNum = prev - left; 
        if (leftNum + 1 == k) {
            return pivot;
        } else if (leftNum + 1 > k) {
            return partition(arr, left, prev - 1, k);
        } else {
            return partition(arr, prev + 1, right, k - (leftNum + 1));
        }
    }
}
1.1.2.2 带注释版本
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int k = scanner.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = scanner.nextInt();
        }
        System.out.println(partition(arr, 0, n - 1, k));
    }

    /**
     * 在数组arr的[left, right]区域找到第k小的数并返回
     * @return 第k小的数
     */
    private static int partition(int[] arr, int left, int right, int k) {
        // 选基准元素
        int pivot = arr[right];
        int prev = left - 1; // 指向小于pivot的最后元素
        int cur = left; // 遍历数组
        while (cur <= right) {
            if (arr[cur] <= pivot) {
                // 将小于等于pivot的元素移至前面
                int tmp = arr[prev + 1];
                arr[prev + 1] = arr[cur];
                arr[cur] = tmp;
                cur++;
                prev++;
            } else {
                // 大于pivot不用移动
                cur++;
            }
        }
        int leftNum = prev - left; // 左半区域元素个数
        if (leftNum + 1 == k) {
            return pivot;
        } else if (leftNum + 1 > k) {
            // 递归左半区域
            return partition(arr, left, prev - 1, k);
        } else {
            // 递归右半区域
            return partition(arr, prev + 1, right, k - (leftNum + 1));
        }
    }
}

1.1.3 扩展题

这里放一些跟本题类似的OJ题（读者可自行尝试解题）：

  1. LeetCode数组中的第K大元素：https://leetcode.cn/problems/xx4gT2/description/
  2. LeetCode最小k个数：https://leetcode.cn/problems/smallest-k-lcci/description/

1.2 题目二：棋盘覆盖

1.2.1 题目信息

题目描述：
在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。
image.png
输入要求：
输入一个整数k，k<=5；
输入特殊格子的坐标x，y。
输出要求：
输出一个由数值表示的二维矩阵。填充规则如下：
（1）用数值填充方格；
（2）特殊方格数值为0；
（3）从中心点开始；然后左上、右上、左下、右下的计数顺序填数；同一块用相同数值表示；
（4）每个数值占4个位置空间；右对齐，左补空格。
输入样例：
3
1 2
输出样例：
image.png
来源：
NBUOJ

1.2.2 算法思路（分治法）

分治策略：首先我们需要明确填充的顺序，根据题目描述填充规则为，从中心点开始，然后按照左上，右上，左下，右下的顺序进行填充
算法步骤：

  1. 首先定义出口条件：只有一个元素时不处理
  2. 找到当前区域的中心点，另四个点位坐标分别是(midRow, midCol)，(midRow, midCol + 1)，(midRow + 1, midCol)，(midRow + 1, midCol + 1)，分别对应四个方位（左上、右上、左下、右下）按照顺序进行处理，**以左上方位举例：**如果说左上存在特殊点，那么特殊点不变继续递归填充dfs(左上, 原特殊点)，但是如果左上方位内部没有特殊点，那么就将当前中心区域的点位作为特殊点继续递归dfs(左上，新特殊点)，此时新特殊点为（midRow, midCol）

示例：也许上面的文字描述有点抽象，还是以画图进行举例：
输入：2 0 3
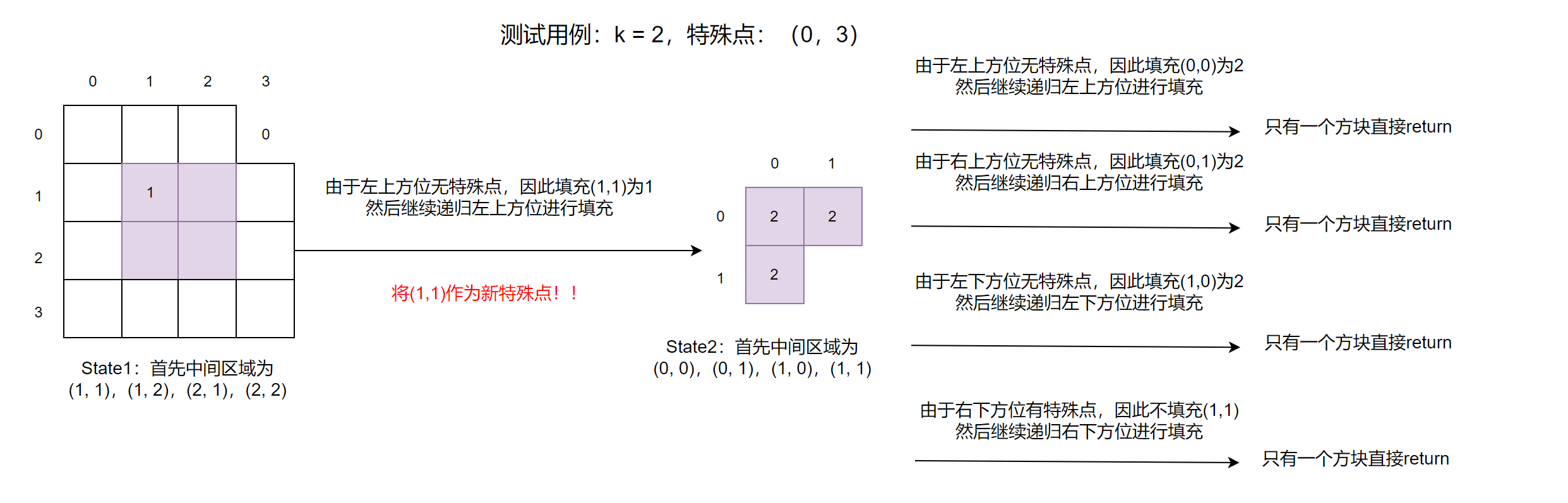
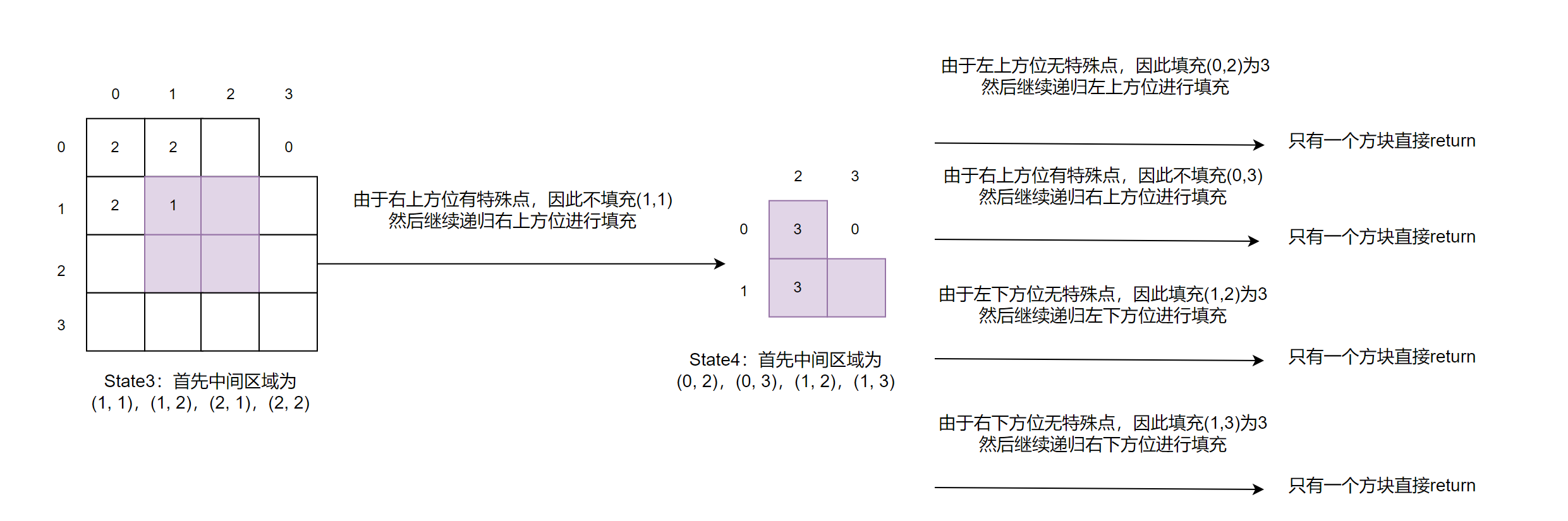
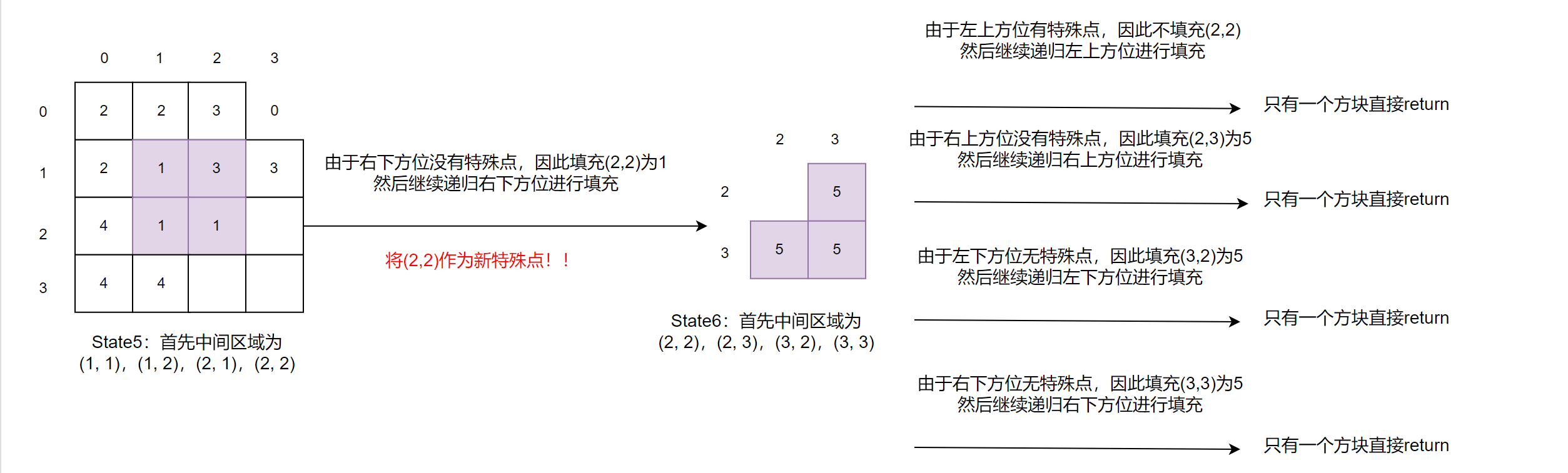
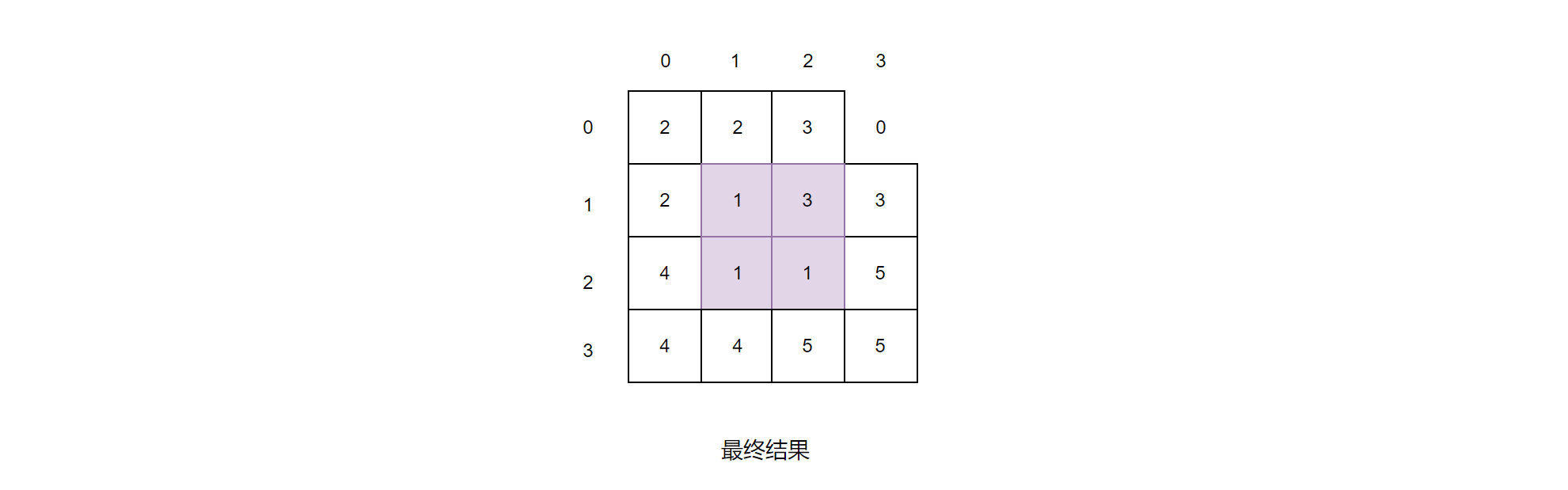
image.png
image.png
image.png
image.png
image.png
注意：如果我们使用成员变量（或者C++中的全局变量），我们需要先维护好中间位置的填充值，然后在递归四个方位，不然有可能出现在递归完左上角后准备填充中间元素的右上区域值时（填充值已经被改变），不过也可以事先全部填充完中间元素再进行递归（看个人习惯）

1.2.3 AC代码（Java实现）

NBUOJ上面Java带中文注释会报错！因此这里放了两个版本的代码，前面不带注释的可以直接跑OJ通过，后面的方便读者阅读

1.2.3.1 不带注释版本
import java.util.Scanner;

public class Main {

    private static int curValue = 1;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            curValue = 1;
            int k = scanner.nextInt();
            int specialRow = scanner.nextInt();
            int specialCol = scanner.nextInt();
            int edges = (int) Math.pow(2, k);
            int[][] matrix = new int[edges][edges];
            matrix[specialRow][specialCol] = 0;
            partition(matrix, 0, edges - 1, 0, edges - 1, specialRow, specialCol);
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[i].length - 1; j++) {
                    System.out.printf("%4s", matrix[i][j]);
                }
                System.out.printf("%4s\n", matrix[i][matrix[i].length - 1]);
            }
        }
    }

    private static void partition(int[][] matrix, int upRow, int downRow, int leftCol, int rightCol, int specialRow, int specialCol) {
        if (upRow == downRow && leftCol == rightCol) {
            return;
        }
        int midValue = curValue;
        curValue++;
        int midLeftUpRow = (upRow + downRow) / 2;
        int midLeftUpCol = (leftCol + rightCol) / 2;
        if (upRow <= specialRow && specialRow <= midLeftUpRow && leftCol <= specialCol && specialCol <= midLeftUpCol) {
            partition(matrix, upRow, midLeftUpRow, leftCol, midLeftUpCol, specialRow, specialCol);
        } else {
            matrix[midLeftUpRow][midLeftUpCol] = midValue;
            partition(matrix, upRow, midLeftUpRow, leftCol, midLeftUpCol, midLeftUpRow, midLeftUpCol);
        }
        int midRightUpRow = midLeftUpRow;
        int midRightUpCol = midLeftUpCol + 1;
        if (upRow <= specialRow && specialRow <= midRightUpRow && midRightUpCol <= specialCol && specialCol <= rightCol) {
            partition(matrix, upRow, midRightUpRow, midRightUpCol, rightCol, specialRow, specialCol);
        } else {
            matrix[midRightUpRow][midRightUpCol] = midValue;
            partition(matrix, upRow, midRightUpRow, midRightUpCol, rightCol, midRightUpRow, midRightUpCol);
        }
        int midLeftDownRow = midLeftUpRow + 1;
        int midLeftDownCol = midLeftUpCol;
        if (midLeftDownRow <= specialRow && specialRow <= downRow && leftCol <= specialCol && specialCol <= midLeftDownCol) {
            partition(matrix, midLeftDownRow, downRow, leftCol, midLeftDownCol, specialRow, specialCol);
        } else {
            matrix[midLeftDownRow][midLeftDownCol] = midValue;
            partition(matrix, midLeftDownRow, downRow, leftCol, midLeftDownCol, midLeftDownRow, midLeftDownCol);
        }
        int midRightDownRow = midLeftUpRow + 1;
        int midRightDownCol = midLeftUpCol + 1;
        if (midRightDownRow <= specialRow && specialRow <= downRow && midRightDownCol <= specialCol && specialCol <= rightCol) {
            partition(matrix, midRightDownRow, downRow, midRightDownCol, rightCol, specialRow, specialCol);
        } else {
            matrix[midRightDownRow][midRightDownCol] = midValue;
            partition(matrix, midRightDownRow, downRow, midRightDownCol, rightCol, midRightDownRow, midRightDownCol);
        }
    }
}
1.2.3.2 带注释版本
import java.util.Scanner;

public class Main {

    private static int curValue = 1;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            // 读取k值
            curValue = 1;
            int k = scanner.nextInt();
            int specialRow = scanner.nextInt(); // 特殊点横坐标
            int specialCol = scanner.nextInt(); // 特殊点纵坐标
            int edges = (int) Math.pow(2, k);
            int[][] matrix = new int[edges][edges];
            matrix[specialRow][specialCol] = 0;
            partition(matrix, 0, edges - 1, 0, edges - 1, specialRow, specialCol);
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[i].length - 1; j++) {
                    System.out.printf("%4s", matrix[i][j]);
                }
                System.out.printf("%4s\n", matrix[i][matrix[i].length - 1]);
            }
        }
    }

    /**
     *
     * @param matrix 矩阵
     * @param upRow 行的上界
     * @param downRow 行的下界
     * @param leftCol 列的左边界
     * @param rightCol 列的右边界
     * @param specialRow 特殊点横坐标
     * @param specialCol 特殊点纵坐标
     */
    private static void partition(int[][] matrix, int upRow, int downRow, int leftCol, int rightCol, int specialRow, int specialCol) {
        if (upRow == downRow && leftCol == rightCol) {
            // 只有一个元素，直接返回
            return;
        }
        // 计算中心区域
        // 维护中间区域填充值
        int midValue = curValue;
        curValue++;
        int midLeftUpRow = (upRow + downRow) / 2;
        int midLeftUpCol = (leftCol + rightCol) / 2;
        if (upRow <= specialRow && specialRow <= midLeftUpRow && leftCol <= specialCol && specialCol <= midLeftUpCol) {
            // 特殊点在左上区域
            partition(matrix, upRow, midLeftUpRow, leftCol, midLeftUpCol, specialRow, specialCol);
        } else {
            matrix[midLeftUpRow][midLeftUpCol] = midValue;
            partition(matrix, upRow, midLeftUpRow, leftCol, midLeftUpCol, midLeftUpRow, midLeftUpCol);
        }
        int midRightUpRow = midLeftUpRow;
        int midRightUpCol = midLeftUpCol + 1;
        if (upRow <= specialRow && specialRow <= midRightUpRow && midRightUpCol <= specialCol && specialCol <= rightCol) {
            // 特殊点在右上区域
            partition(matrix, upRow, midRightUpRow, midRightUpCol, rightCol, specialRow, specialCol);
        } else {
            matrix[midRightUpRow][midRightUpCol] = midValue;
            partition(matrix, upRow, midRightUpRow, midRightUpCol, rightCol, midRightUpRow, midRightUpCol);
        }
        int midLeftDownRow = midLeftUpRow + 1;
        int midLeftDownCol = midLeftUpCol;
        if (midLeftDownRow <= specialRow && specialRow <= downRow && leftCol <= specialCol && specialCol <= midLeftDownCol) {
            // 特殊点在左下区域
            partition(matrix, midLeftDownRow, downRow, leftCol, midLeftDownCol, specialRow, specialCol);
        } else {
            matrix[midLeftDownRow][midLeftDownCol] = midValue;
            partition(matrix, midLeftDownRow, downRow, leftCol, midLeftDownCol, midLeftDownRow, midLeftDownCol);
        }
        int midRightDownRow = midLeftUpRow + 1;
        int midRightDownCol = midLeftUpCol + 1;
        if (midRightDownRow <= specialRow && specialRow <= downRow && midRightDownCol <= specialCol && specialCol <= rightCol) {
            // 特殊点在右下区域
            partition(matrix, midRightDownRow, downRow, midRightDownCol, rightCol, specialRow, specialCol);
        } else {
            matrix[midRightDownRow][midRightDownCol] = midValue;
            partition(matrix, midRightDownRow, downRow, midRightDownCol, rightCol, midRightDownRow, midRightDownCol);
        }
    }
}

1.3 题目三：求逆序对

1.3.1 题目信息

题目描述：
给定一个序列a1,a2,…,an，如果存在i<j并且ai>aj，那么我们称之为逆序对，求逆序对的数目。
要求用分治法求解。
输入要求：
第一行为n,表示序列长度；
接下来的n行，第i+1行表示序列中的第i个数。/或者第2行有n个数。
输出要求：
所有逆序对总数
输入样例：
4
3
2
3
2
输出样例：
3
来源：
NBUOJ

1.3.2 算法思路（分治法）

这里直接给大家介绍算法思路了：
模板：归并排序
算法步骤（重要）：

  1. 我们设计一个递归函数partition(int[] arr, int left, int right)求解区间内逆序对的个数并且完成排序功能
  2. 然后我们将数组划分为两个区间[left, mid]，[mid + 1, right]
  3. 递归调用partition(arr, left, mid)此时将左半部分区间逆序对统计完毕并且排序完成，递归调用partition(arr, mid + 1, right)此时将右半部分区间逆序对统计完毕并且排序完成
  4. 此时我们只需要统计排序完毕的左区间和排序完毕后右区间之间的逆序对个数了

PS：上述代码基于归并排序的模板实现，下面着重讲解如何统计两个排序完毕区间之间的逆序对个数
示例：测试用例：[1, 5, 2, 7, 4, 3, 0, 6] 画图讲解：
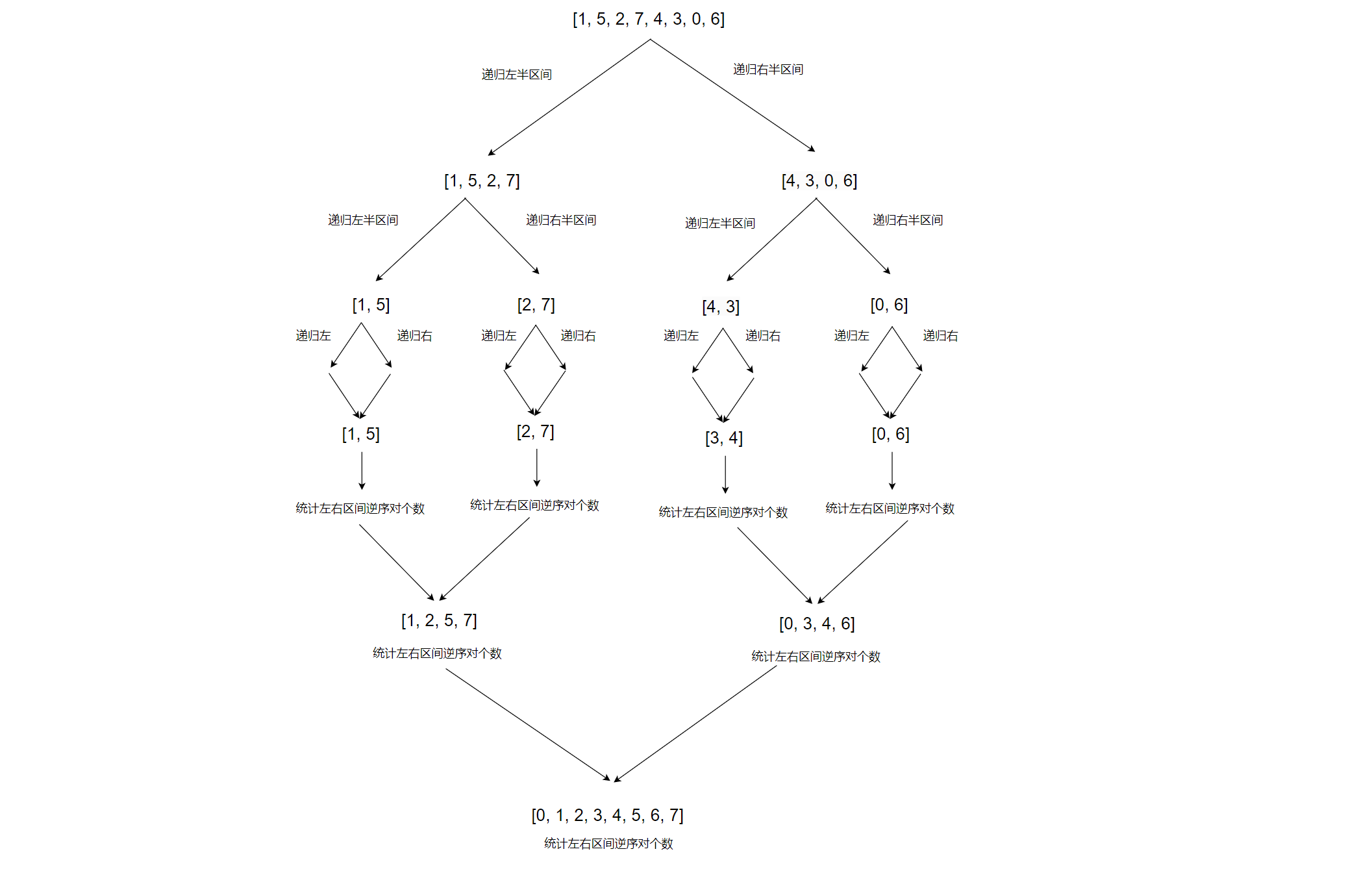
image.png
上图所示是递归与回溯的示意图：下面我们专门讲解两个有序区间内部如何统计逆序对的问题

PS：与上图示意图有所不一致的是，统计逆序对的问题在归并排序的时候最好使用降序排序，至于为什么，大家下来自己尝试一下嘻嘻！

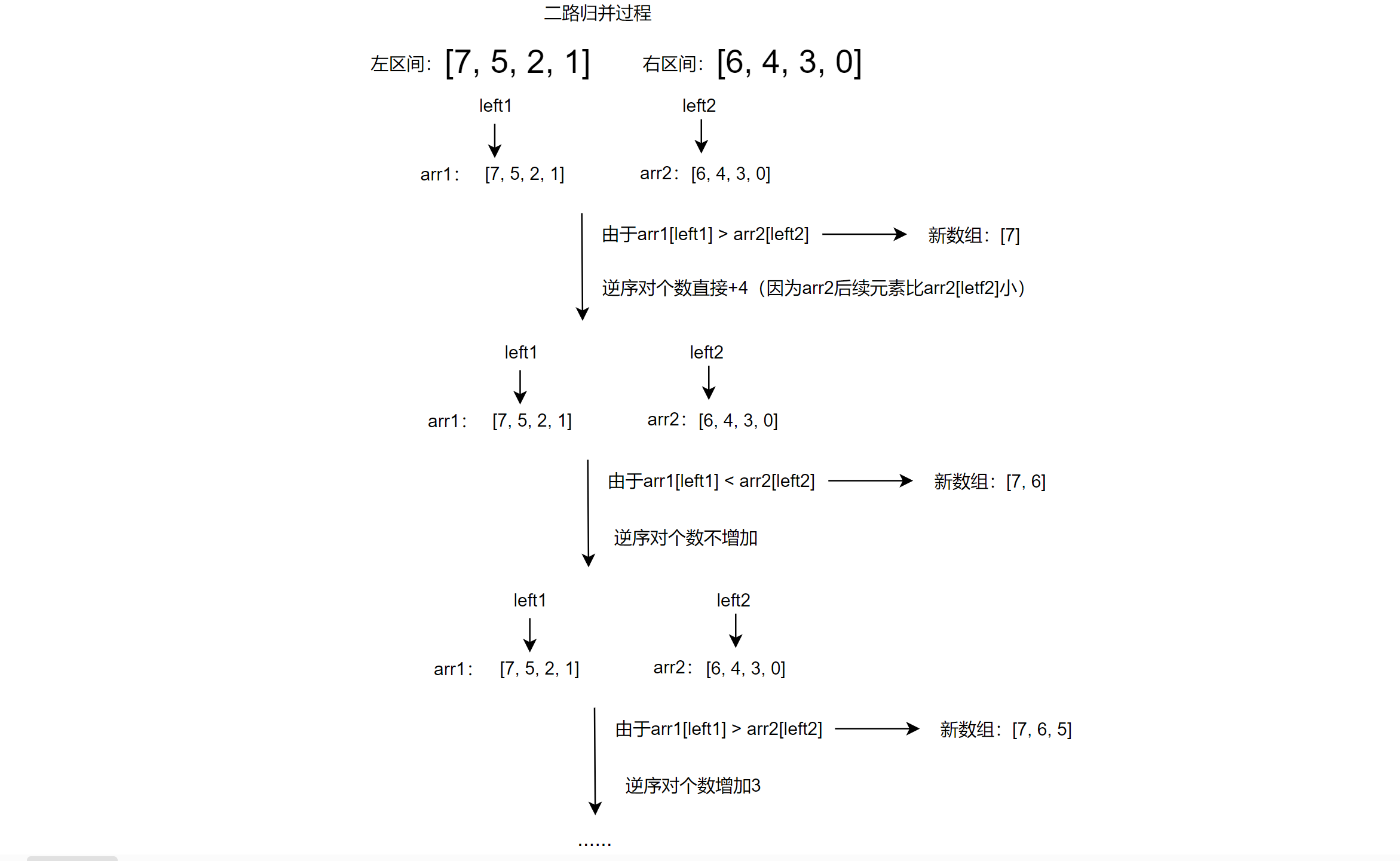
image.png
此时相比聪明的大家已经可以想明白过程了（事实上就是在二路归并中进行逆序对的统计，并且只有左区间的当前元素大于右区间当前元素时才会统计），当左区间全部遍历完毕后，两个区间之间的逆序对个数就统计完毕了！

1.3.3 AC代码（Java实现）

NBUOJ上面Java带中文注释会报错！因此这里放了两个版本的代码，前面不带注释的可以直接跑OJ通过，后面的方便读者阅读

1.3.3.1 不带注释版本
import java.util.Scanner;

public class Main {
    private static int reversePairCount = 0;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            reversePairCount = 0;
            int n = scanner.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = scanner.nextInt();
            }
            partition(arr, 0, n - 1);
            System.out.println(reversePairCount);
        }
    }

    private static void partition(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int mid = (left + right) / 2;
        partition(arr, left, mid);
        partition(arr, mid + 1, right);
        int[] tmp = new int[right - left + 1];
        int tmpIndex = 0;
        int left1 = left;
        int right1 = mid;
        int left2 = mid + 1;
        int right2 = right;
        while (left1 <= right1 && left2 <= right2) {
            if (arr[left1] > arr[left2]) {
                tmp[tmpIndex++] = arr[left1];
                left1++;
                reversePairCount += (right2 - left2 + 1);
            } else {
                tmp[tmpIndex++] = arr[left2];
                left2++;
            }
        }
        while (left1 <= right1) {
            tmp[tmpIndex++] = arr[left1];
            left1++;
        }
        while (left2 <= right2) {
            tmp[tmpIndex++] = arr[left2];
            left2++;
        }
        for (int i = 0; i < tmpIndex; i++) {
            arr[left + i] = tmp[i];
        }
    }
}
1.3.3.2 带注释版本
import java.util.Scanner;

public class Main {
    private static int reversePairCount = 0;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            reversePairCount = 0;
            int n = scanner.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = scanner.nextInt();
            }
            partition(arr, 0, n - 1);
            System.out.println(reversePairCount);
        }
    }

    /**
     * 统计区间[left, right]内部逆序对的个数
     * @param arr 数组元素
     * @param left 左区间
     * @param right 右区间
     */
    private static void partition(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        // 计算中心下标
        int mid = (left + right) / 2;
        partition(arr, left, mid); // 统计左区间逆序对个数并排序
        partition(arr, mid + 1, right); // 统计右区间逆序对个数并排序
        int[] tmp = new int[right - left + 1]; // 临时数组
        int tmpIndex = 0;
        int left1 = left;
        int right1 = mid;
        int left2 = mid + 1;
        int right2 = right;
        while (left1 <= right1 && left2 <= right2) {
            if (arr[left1] > arr[left2]) {
                tmp[tmpIndex++] = arr[left1];
                left1++;
                reversePairCount += (right2 - left2 + 1);
            } else {
                tmp[tmpIndex++] = arr[left2];
                left2++;
            }
        }
        while (left1 <= right1) {
            tmp[tmpIndex++] = arr[left1];
            left1++;
        }
        while (left2 <= right2) {
            tmp[tmpIndex++] = arr[left2];
            left2++;
        }
        // 拷贝回原数组
        for (int i = 0; i < tmpIndex; i++) {
            arr[left + i] = tmp[i];
        }
    }
}

1.3.4 扩展题

这里放一些跟本题类似的OJ题（读者可自行尝试解题）：

  1. LeetCode交易逆序对的总数：https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
  2. LeetCode翻转对：https://leetcode.cn/problems/reverse-pairs/description/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1523949.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Web开发】CSS教学(超详细,满满的干货)

【Web开发】CSS教学(超详细,满满的干货)

&#x1f493; 博客主页&#xff1a;从零开始的-CodeNinja之路 ⏩ 收录文章&#xff1a;【Web开发】CSS教学(超详细,满满的干货) &#x1f389;欢迎大家点赞&#x1f44d;评论&#x1f4dd;收藏⭐文章 目录 CSS一. 什么是CSS?1.1 基本语法规范1.2 引入方式1.3 规范 二. CSS选…
阅读更多...
JavaScript练手小技巧：数字反转时钟

JavaScript练手小技巧：数字反转时钟

样式基于博主的这篇文章&#xff1a; CSS3技巧38&#xff1a;3D 翻转数字效果-CSDN博客 既然可以实现翻转数字了&#xff0c;肯定就可以跟 JS 相结合去完成一些数字展示效果。 比如&#xff0c;数字反转时钟。 为了方便&#xff0c;所有 HTML 数字根据时间动态生成。因此&a…
阅读更多...
从排序算法的艺术看C语言qsort函数的魅力：一场数据的时空穿越

从排序算法的艺术看C语言qsort函数的魅力：一场数据的时空穿越

欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看&#xff0c;已成习惯 创作不易&#xff0c;多多支持&#xff01; 目录 一 、回调函数 二、qsort函数 1.qsort函数排序整型数据 2.qsort函数排序结构数据 一 、回调函数 何为回调函数&#xff1…
阅读更多...
【JS进阶】第一天

【JS进阶】第一天

参考视频——黑马程序员 JavaScript 进阶 - 第 1 天 学习作用域、变量提升、闭包等语言特征&#xff0c;加深对 JavaScript 的理解&#xff0c;掌握变量赋值、函数声明的简洁语法&#xff0c;降低代码的冗余度。 理解作用域对程序执行的影响能够分析程序执行的作用域范围理解闭…
阅读更多...
三维坐标系之间的转换

三维坐标系之间的转换

一、概括 这个完全是抄别人的&#xff0c;给我自己看的主要是想当我要看的时候我直接能找到&#xff0c;而不用再去网上搜索&#xff0c;后期会吧代码更新上去。 彻底搞懂“旋转矩阵/欧拉角/四元数”&#xff0c;让你体会三维旋转之美_欧拉角判断动作-CSDN博客 在不同的坐标…
阅读更多...
Python语法糖

Python语法糖

N u m P y NumPy NumPy的 n d i t e r nditer nditer nditer 是 NumPy 提供的一种多维迭代器&#xff0c;用于对多维数组进行迭代操作。它可以替代传统的嵌套循环&#xff0c;在处理多维数组时更加方便和高效。 迭代器可以按照不同的顺序遍历数组的元素&#xff0c;也可以控制…
阅读更多...
✅技术社区—通过Canal框架实现MySQL与ElasticSearch的数据同步

✅技术社区—通过Canal框架实现MySQL与ElasticSearch的数据同步

Canal 是一个由阿里巴巴开源的&#xff0c;基于 Java 的数据库变更日志解析的中间件&#xff0c;其原理是基于Binlog订阅的方式实现&#xff0c;模拟一个MySQL Slave 订阅Binlog日志&#xff0c;从而实现CDC&#xff0c;主要用于实现 MySQL 数据库的增量数据同步。它主要的使用…
阅读更多...
Linux：PostGreSQL|PostGIS部署

Linux：PostGreSQL|PostGIS部署

由于更换了云服务器&#xff0c;需要重新部署PostGreSQL|PostGIS&#xff0c;所以记录一下Linux CentOS 7 x86-64环境下&#xff0c;PostGreSQL|PostGIS的部署过程。 参考文档&#xff1a;PostgreSQL: Linux downloads (Red Hat family)。 yum安装PostGreSQL 通过yum安装PostG…
阅读更多...
PC-DARTS: PARTIAL CHANNEL CONNECTIONS FOR MEMORY-EFFICIENT ARCHITECTURE SEARCH

PC-DARTS: PARTIAL CHANNEL CONNECTIONS FOR MEMORY-EFFICIENT ARCHITECTURE SEARCH

PC-DARTS&#xff1a;用于内存高效架构搜索的部分通道连接 论文链接&#xff1a;https://arxiv.org/abs/1907.05737 项目链接&#xff1a;https://github.com/yuhuixu1993/PC-DARTS ABSTRACT 可微分体系结构搜索(DARTS)在寻找有效的网络体系结构方面提供了一种快速的解决方案…
阅读更多...
网络编程-套接字相关基础知识

网络编程-套接字相关基础知识

1.1. Socket简介 套接字&#xff08;socket&#xff09;是一种通信机制&#xff0c;凭借这种机制&#xff0c; 客户端<->服务器 模型的通信方式既可以在本地设备上进行&#xff0c;也可以跨网络进行。 Socket英文原意是“孔”或者“插座”的意思&#xff0c;在网络编程…
阅读更多...
ROS——ROS安装遇到的问题

ROS——ROS安装遇到的问题

1、添加ROS软件源 打开终端&#xff0c;将下面这条命令复制到ubuntu的终端执行 sudo sh -c . /etc/lsb-release && echo "deb http://mirrors.ustc.edu.cn/ros/ubuntu/ $DISTRIB_CODENAME main" > /etc/apt/sources.list.d/ros-latest.list2、添加密钥 …
阅读更多...
Java面试题总结200道(三)

Java面试题总结200道(三)

51、什么是 Spring IOC 容器 Spring 框架的核心是 Spring 容器。容器创建对象&#xff0c;将它们装配在一起&#xff0c;配置它 们并管理它们的完整生命周期。Spring 容器使用依赖注入来管理组成应用程序的 组件。容器通过读取提供的配置元数据来接收对象进行实例化&#xff0…
阅读更多...
Windows Docker 部署 Solr 搜索引擎

Windows Docker 部署 Solr 搜索引擎

一、简介 Solr 是 Apache 下的一个顶级开源项目&#xff0c;采用 Java 开发&#xff0c;它是基于 Lucene 的全文搜索服务器。Solr 可以独立运行在 Jetty、Tomcat 等这些 Servlet 容器中。Solr 提供了比 Lucene 更为丰富的查询语言&#xff0c;同时实现了可配置、可扩展&#x…
阅读更多...
OpenHarmony4.0对RK3566的烧写过程

OpenHarmony4.0对RK3566的烧写过程

前面已经编译的过程搞了比较长的时间，因为遇到了不少问题，老是编译出错，后来经过努力还是编译成功了。 我这里主要针对RK3566的Purple Pi OH开发板，如下图： 因为开源鸿蒙里没有针对这个板的特殊配置，需要下载下面这个文件： purple-pi-oh-patch.zip 这个文件里包含了可…
阅读更多...
（二）OpenOFDM频偏校正

（二）OpenOFDM频偏校正

频偏校正 This paper [1]解释了频率偏移发生的原因以及如何纠正它。简而言之&#xff0c;有两种类型的频率偏移。第一个称为载波频率偏移 (CFO)&#xff0c;是由发射器和接收器的本地振荡器 (LO) 之间的差异引起的。这种偏移的症状是输入 I/Q 样本&#xff08;时域&#xff09…
阅读更多...
国际前十正规外汇实时行情走势app软件最新排名（综合版）

国际前十正规外汇实时行情走势app软件最新排名（综合版）

外汇交易&#xff0c;作为当今世界金融市场上一个重要的板块&#xff0c;备受关注和热议。随着金融市场的日益发展&#xff0c;外汇交易也发展成为一个新兴的投资交易渠道。为了更好地满足投资者对外汇市场的需求&#xff0c;外汇实时行情走势app软件应运而生&#xff0c;它为投…
阅读更多...
R语言聚类分析-K均值聚类与系统聚类法

R语言聚类分析-K均值聚类与系统聚类法

一、数据集为firm.csv&#xff0c;给出了22家美国公用事业公司的相关数据集&#xff0c;各数据集变量的名称和含义如下&#xff1a;X1为固定费用周转比&#xff08;收入/债务&#xff09;&#xff0c;X2为资本回报率&#xff0c;X3为每千瓦容量成本&#xff0c;X4为年载荷因子&…
阅读更多...
YOLOv9详解

YOLOv9详解

1.概述 在逐层进行特征提取和空间转换的过程中&#xff0c;会损失大量信息&#xff0c;例如图中的马在建模过程中逐渐变得模糊&#xff0c;从而影响到最终的性能。YOLOv9尝试使用可编程梯度信息PGI解决这一问题。 具体来说&#xff0c; PGI包含三个部分&#xff0c;&#xff0…
阅读更多...
LeetCode每日一题[C++]-310.最小高度树

LeetCode每日一题[C++]-310.最小高度树

题目描述 树是一个无向图&#xff0c;其中任何两个顶点只通过一条路径连接。 换句话说&#xff0c;一个任何没有简单环路的连通图都是一棵树。 给你一棵包含 n 个节点的树&#xff0c;标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表&#xff08;每一个…
阅读更多...
数据过滤的练习

数据过滤的练习

定义一个集合&#xff0c;并添加一些整数1&#xff0c;2&#xff0c;3&#xff0c;4&#xff0c;5&#xff0c;6&#xff0c;7&#xff0c;8&#xff0c;9&#xff0c;10&#xff0c;过滤奇数&#xff0c;只留下偶数&#xff0c;并将结果保存起来。 package MyStream;import j…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023