一、概括

这个完全是抄别人的，给我自己看的主要是想当我要看的时候我直接能找到，而不用再去网上搜索，后期会吧代码更新上去。

彻底搞懂“旋转矩阵/欧拉角/四元数”，让你体会三维旋转之美_欧拉角判断动作-CSDN博客

在不同的坐标系中物体的位姿是相对的，任何的坐标系都是相对来说的，那么为什么要坐标系做转换呢？其主要的一个原因是为了更好的测量或者更好的识别。

我们常说的世界坐标系（world ） 也是相对的，我们知道地球绕着太阳转  太阳也在绕这（银河）别的坐标系来旋转，而且是在越来越远离坐标系原点的，所以我们物质的真个世界都是相对的。这个在古代的天干地支中就已经有体现了 。

从小的方面来说我们的导航系统 就是我们在驾驶的时候坐标系中各个物体在切换，坐标系在变换。如：

二、旋转矩阵

为什么要坐标系转换？

简单的说就是为了更好的测量与识别，这是一个从局部到全局（也是相对的）的变换。

坐标系转换需要什么东西？

在从一个坐标系到另外一个坐标系的过程中我们需要一个桥梁，那就是世界坐标系，如下：

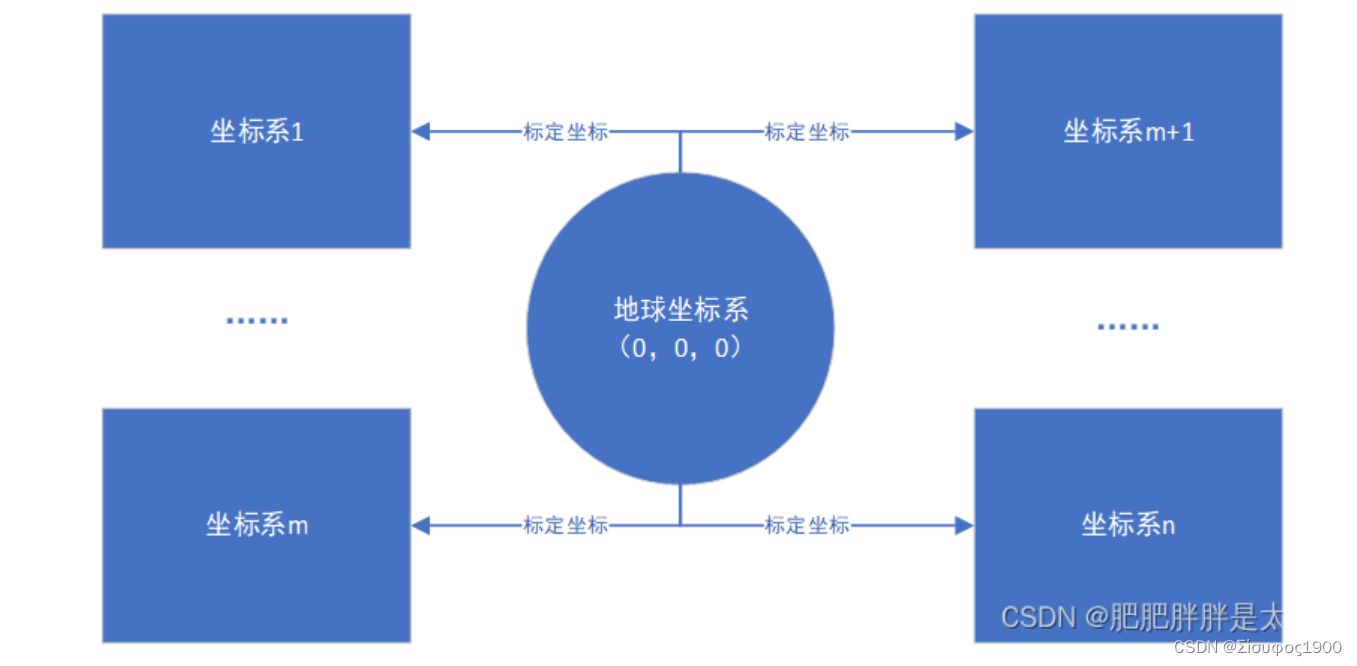
坐标系转换：

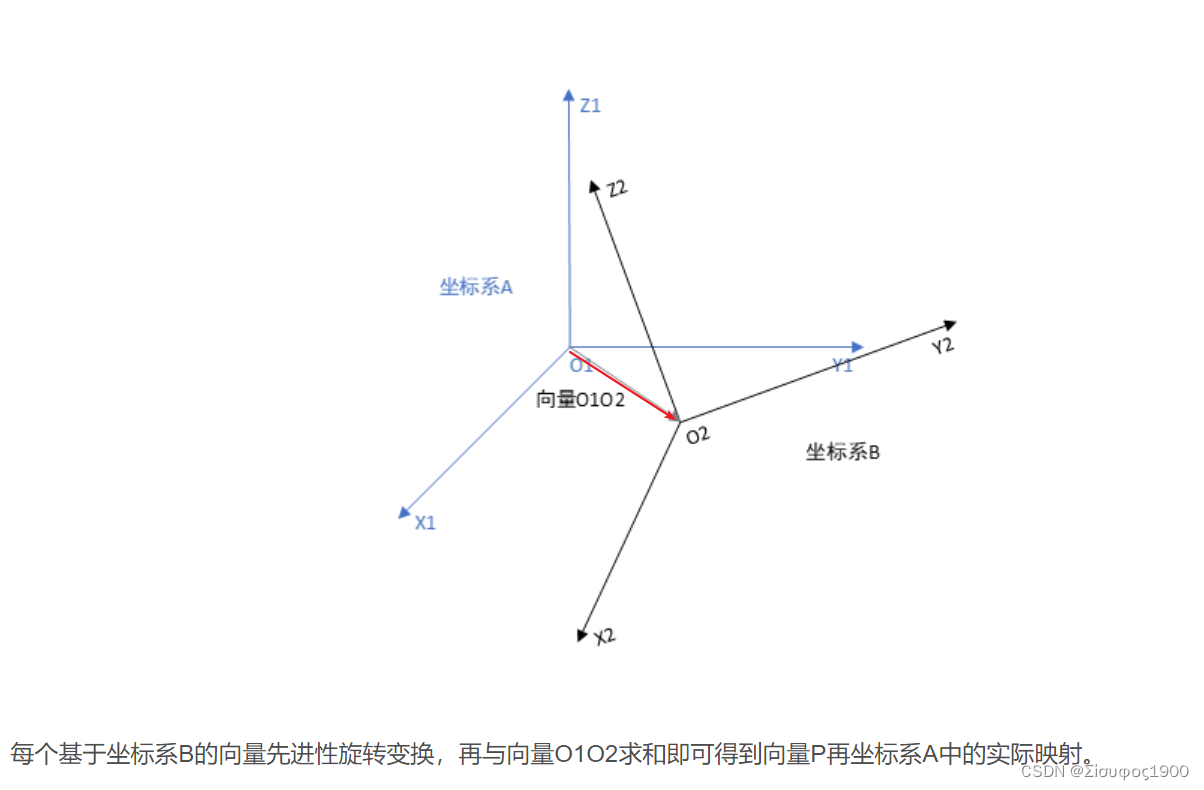
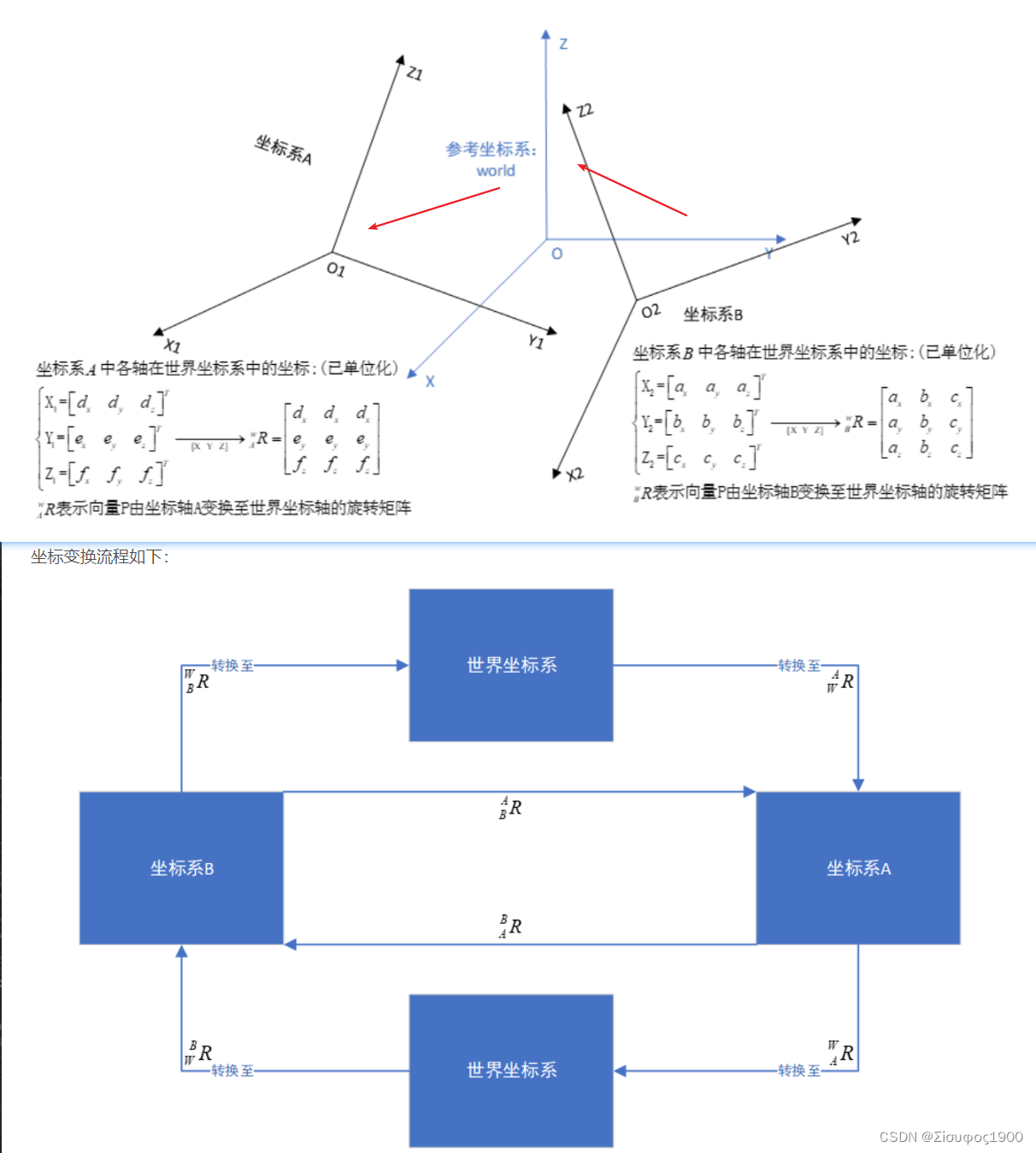
从O1 ->O2 坐标系的转换 ，如图：

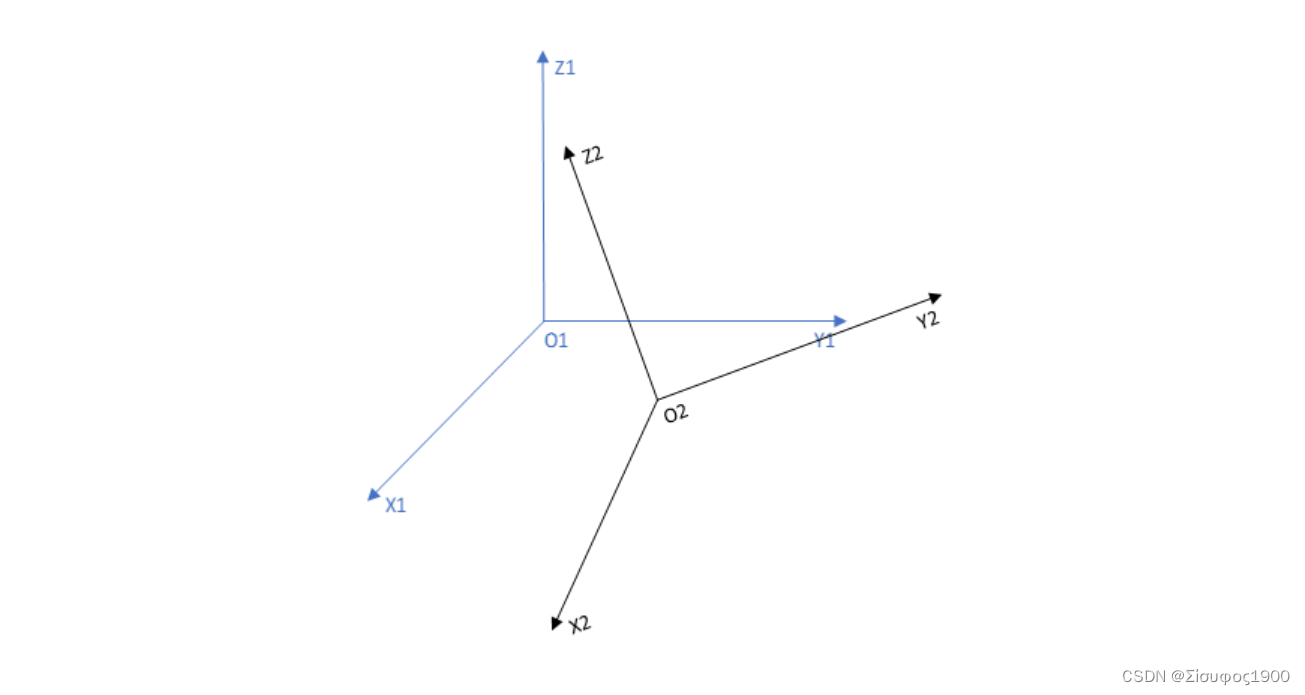
我们可以理解为先平移，然后再旋转

 向量分解

我们把一个向量可以分解到三个不同的方向上，其实就是在 X Y Z方向上做投影，

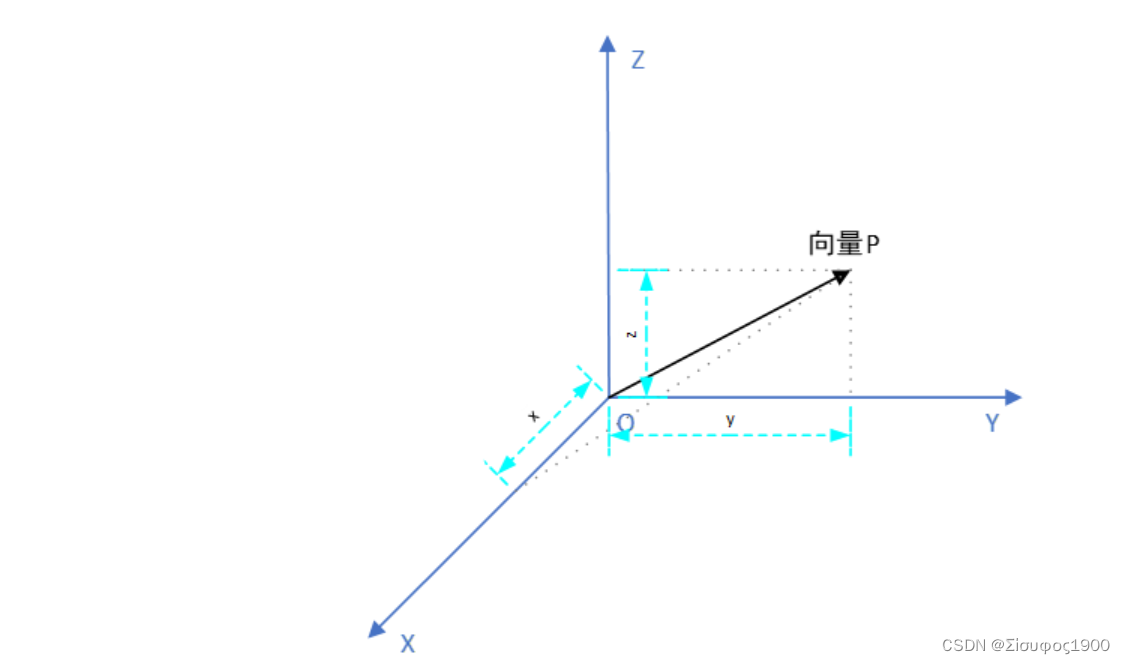
单位向量在坐标系中的投影

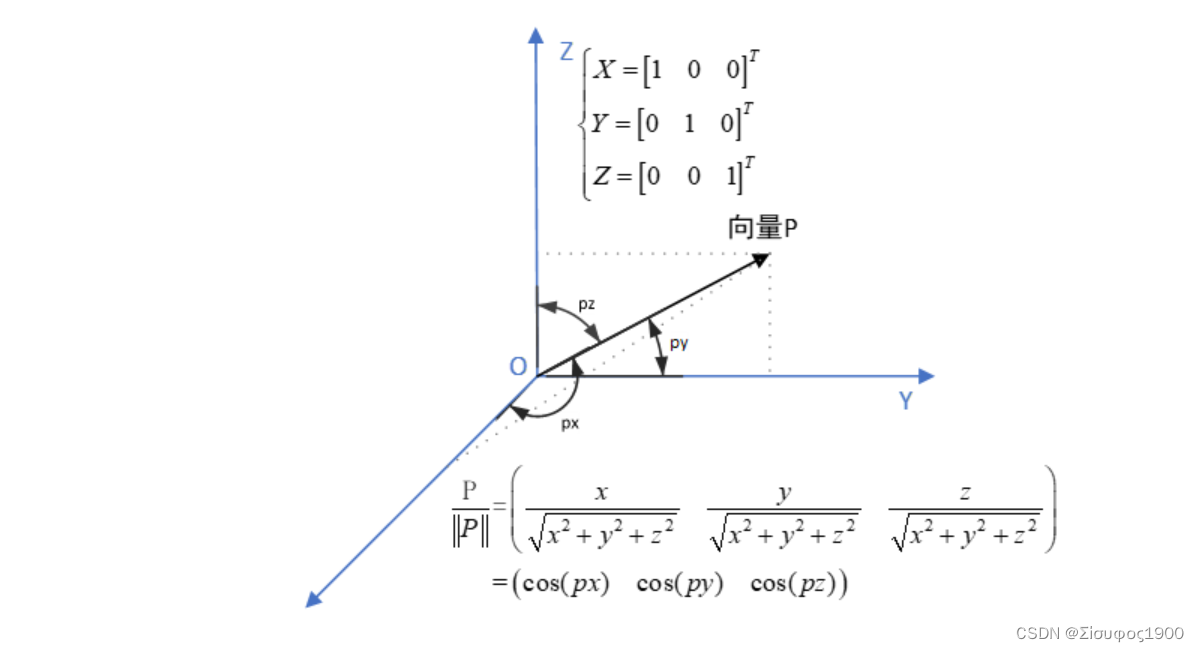
那么 同一个点在不同的坐标系下的坐标是：

 P在A 坐标系下的坐标是   {xa ，ya，za}

同理在 B坐标系下的位置 是 {xb ，yb，zb}  

那么 我们可以产生一个旋转矩阵  b->b R（表示在b坐标系的点转换到A坐标下的）旋转矩阵

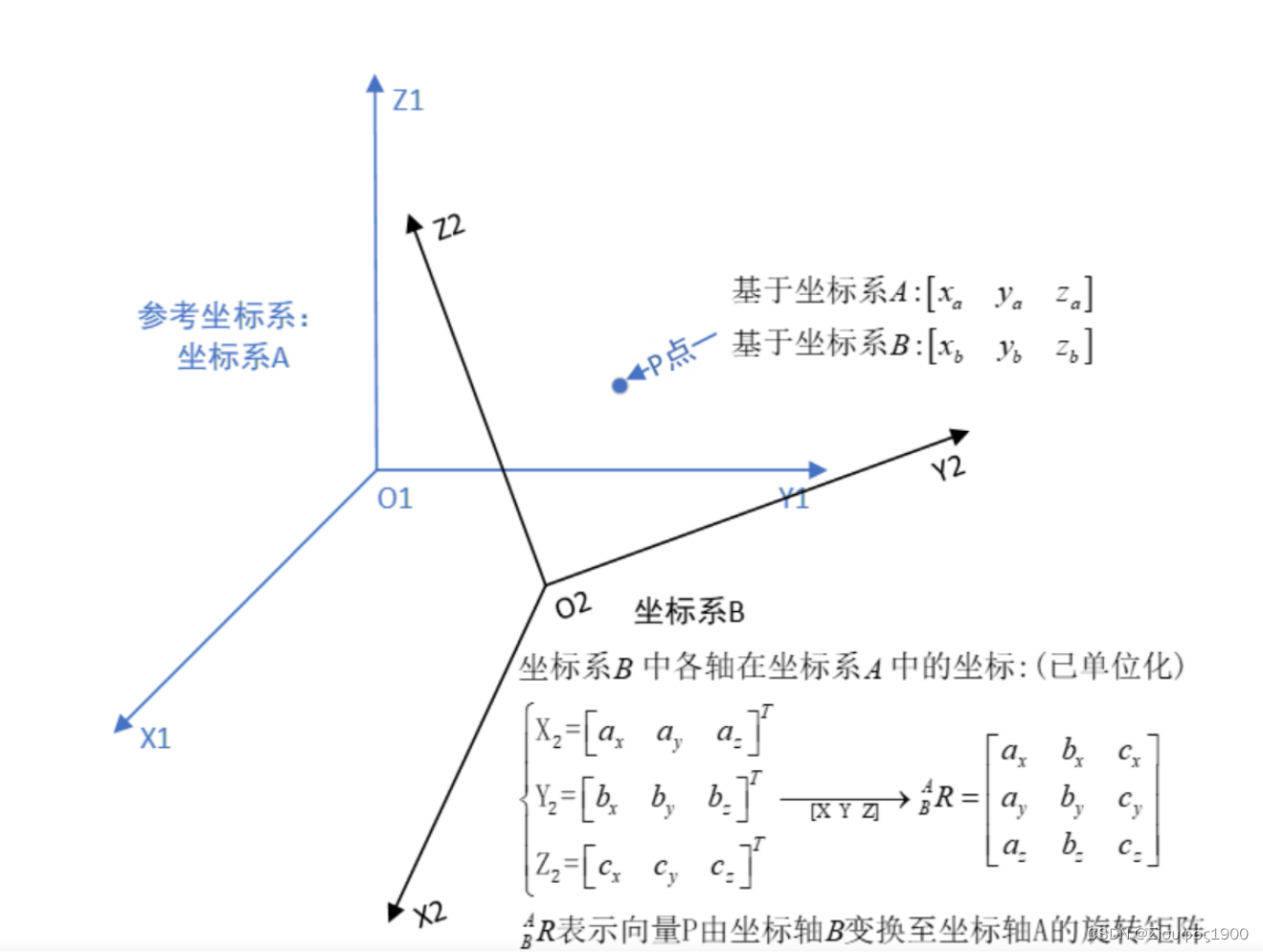
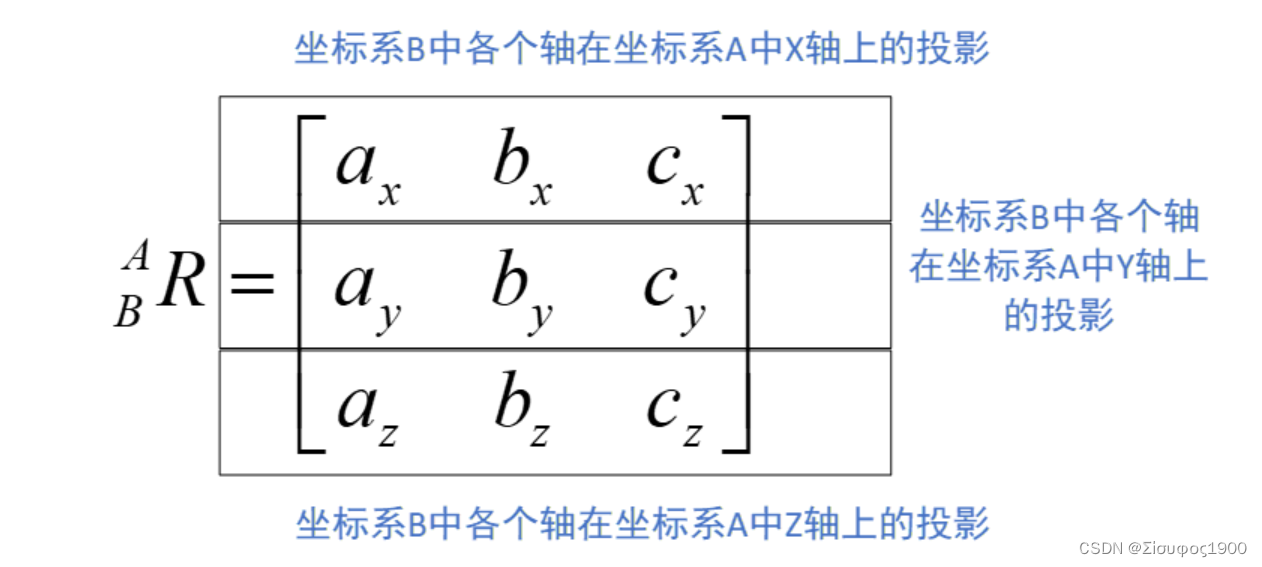
向量坐标的计算无非就是投影，那么向量坐标从坐标系B转换至坐标系A无非就是两次投影而已：

 

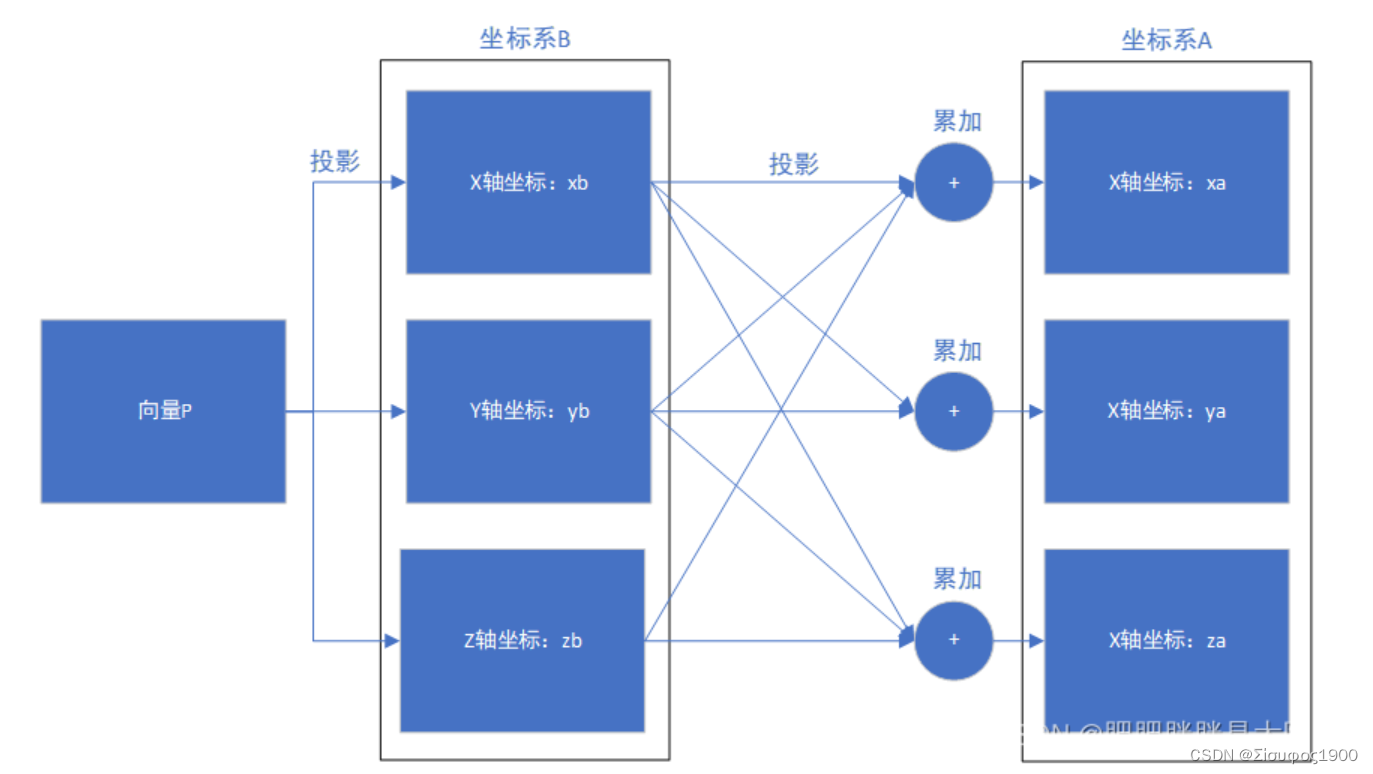
 坐标变换中平移的实质

向量可以在坐标系中任意移动，只要不改变向量的方向和大小，向量的属性不会发生变化。但是我们研究的是坐标系B中一个坐标点在坐标系A中的映射，因此需要考虑坐标系B的原点O2相较于坐标系A原点O1平移的距离。

如何计算坐标系B各坐标轴在坐标系A上的投影？（多坐标变换）

如何实现坐标变换？ 

有了上面的解释，我们可以计算出一个矩阵：

三、欧拉角 

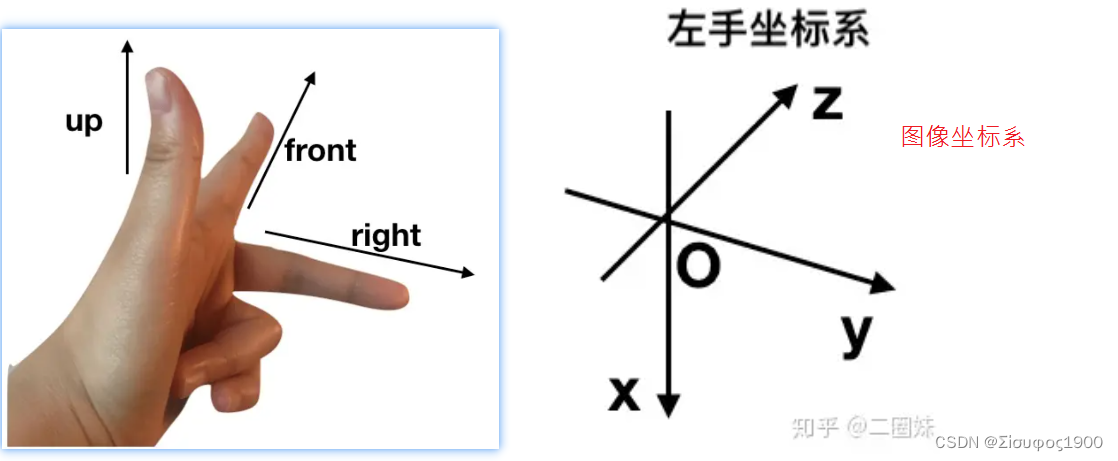
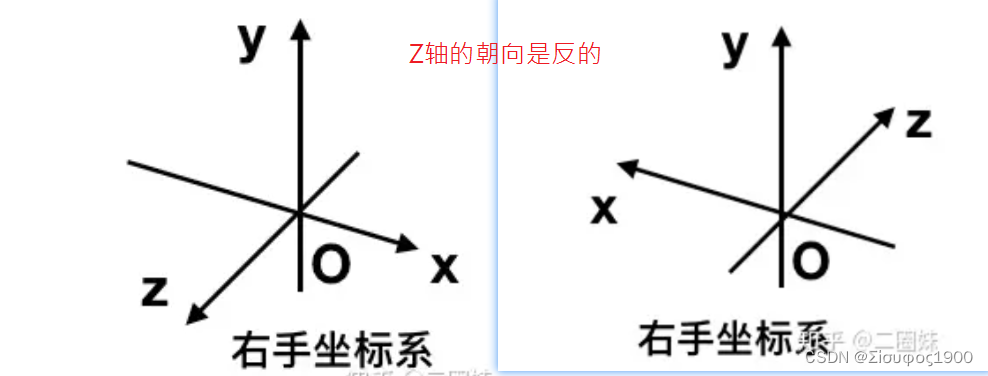
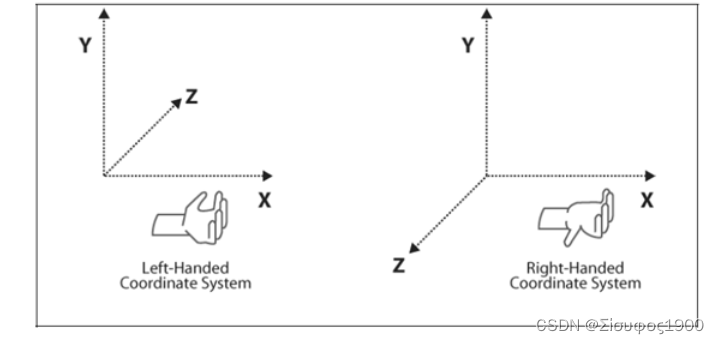
左手 和右手 坐标系

左手坐标系

 右手坐标系

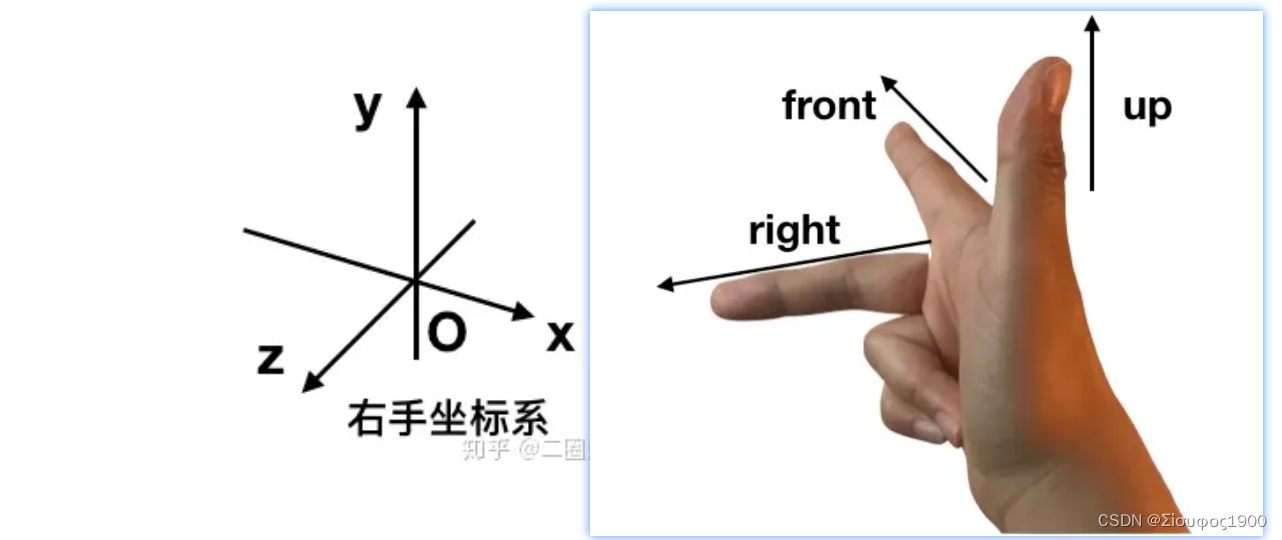
对比一下：

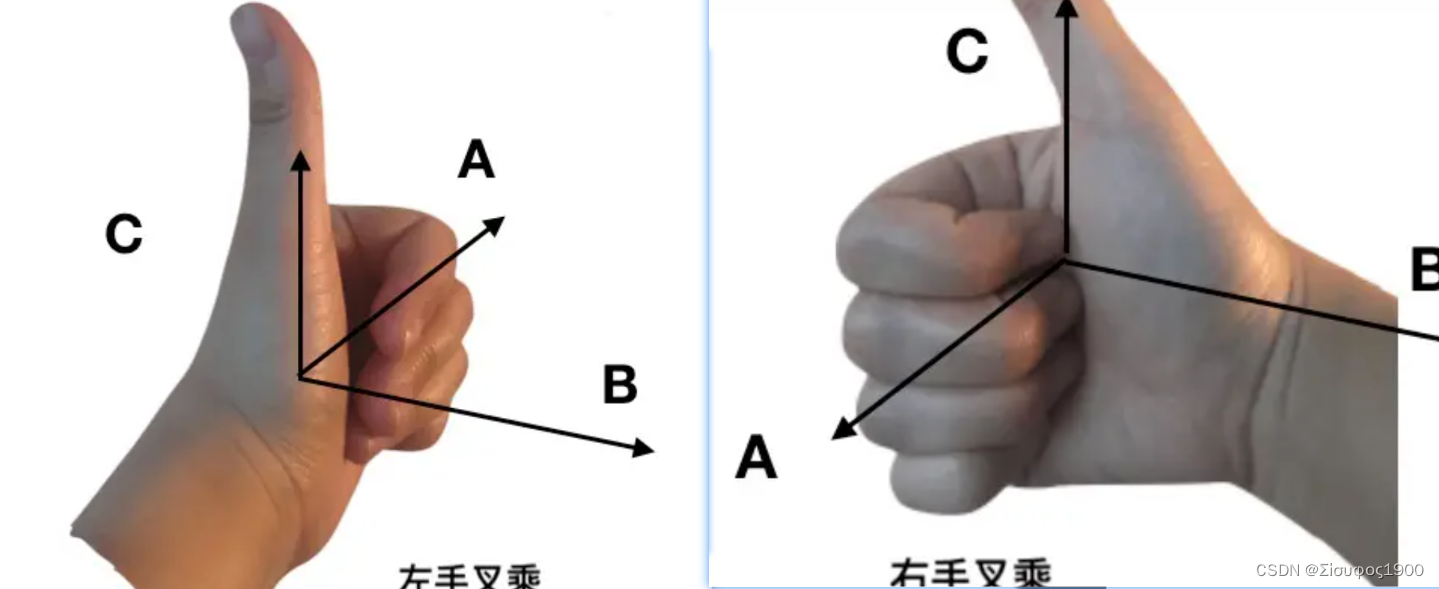
 叉乘

 

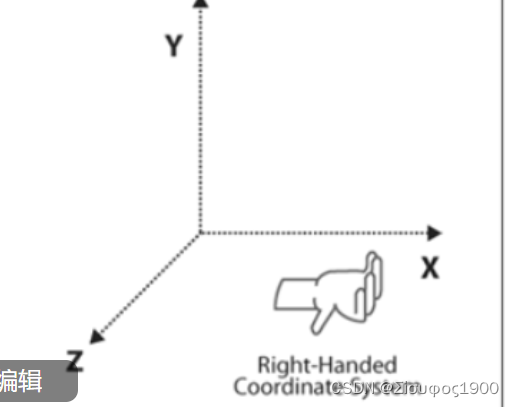
Maya 和 OPenGL 使用右手坐标系， DirectX, pbrt， PRMan 使用左手坐标系。

欧拉角

有三个自由度： 偏航（yaw - z） pitch(俯仰-Y)  roll (翻滚-x)，

一般情况下是按照 Z -Y -X 的顺序来转动的，

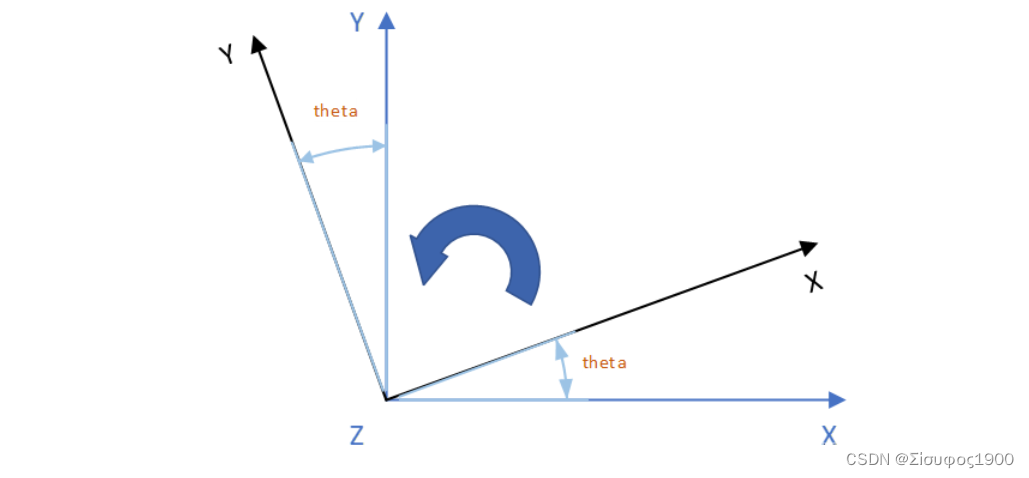
 绕Z轴旋转的话，就是XOY面的上点的转动：

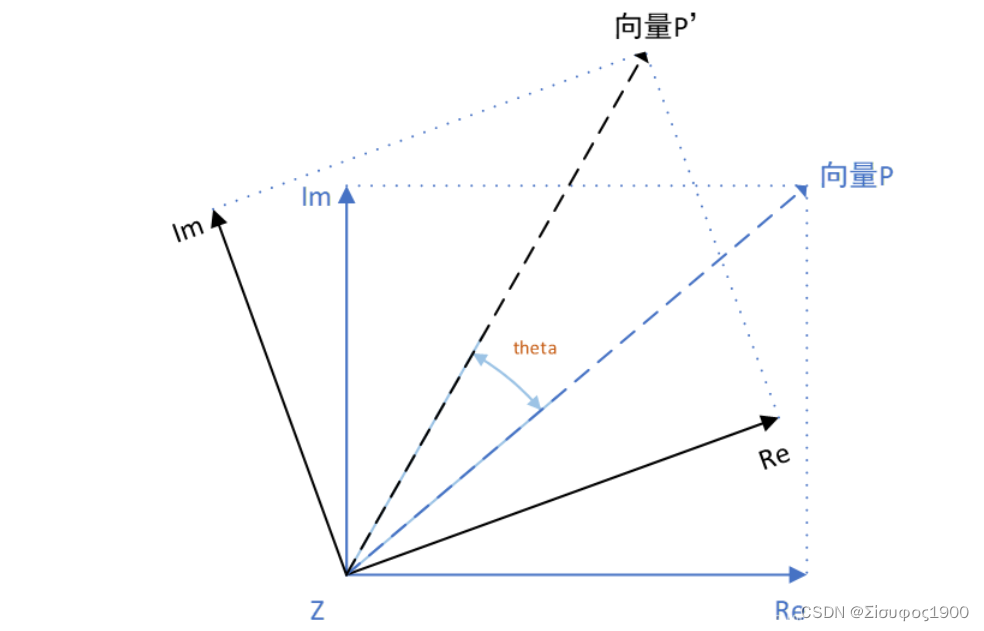
 在这个平面上将向量旋转，然后用矩阵的方式来表示：

欧拉角转化为旋转矩阵

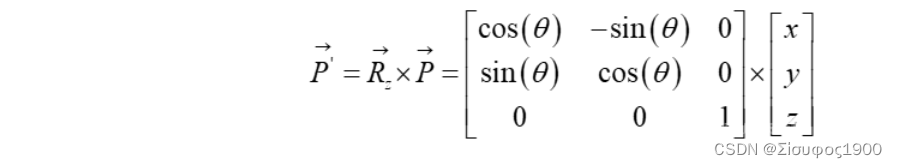
 同理，我们可以按照同样的方式得出到X/Y轴旋转的公式：

 

外旋（x->y->z）和内旋（z->y->x），我们一般使用外旋的顺序（halcon 里面使用的好像是内旋）

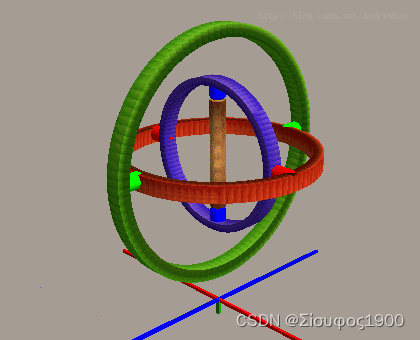
欧拉角的弊端---万向锁 

就是当任何一个方向转到90 度的时候会和另外两个自由度中的两个重合，导致会失去一个自由度，然后当我们要使用失去按个自由度的时候，用到了其他的自由度，这就构成了万向锁，如下图：

因此为了解决万向锁的问题，在三个自由度的基础上添加了一个自由度，就是4个自由度---即四元数 

四、四元数