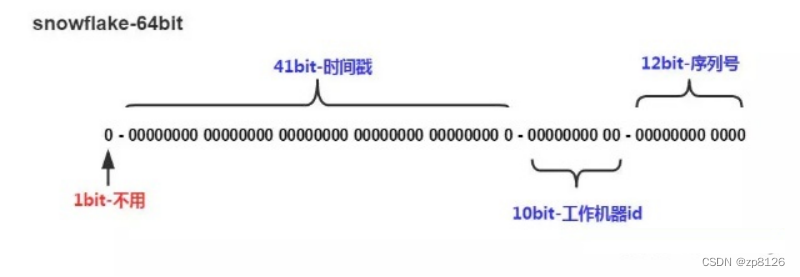
频偏校正
This paper [1]解释了频率偏移发生的原因以及如何纠正它。简而言之,有两种类型的频率偏移。第一个称为载波频率偏移 (CFO),是由发射器和接收器的本地振荡器 (LO) 之间的差异引起的。这种偏移的症状是输入 I/Q 样本(时域)的相位旋转。第二个是采样频率偏移(SFO),是由采样效应引起的。这种偏移的症状是FFT(频域)后星座点的相位旋转。
CFO 可以借助短前导码(粗略)和长前导码(精细)进行校正。并且可以使用每个OFDM符号中的导频子载波来校正SFO。在我们了解校正是如何完成之前。让我们直观地看看每个校正步骤如何帮助最终的星座平面。
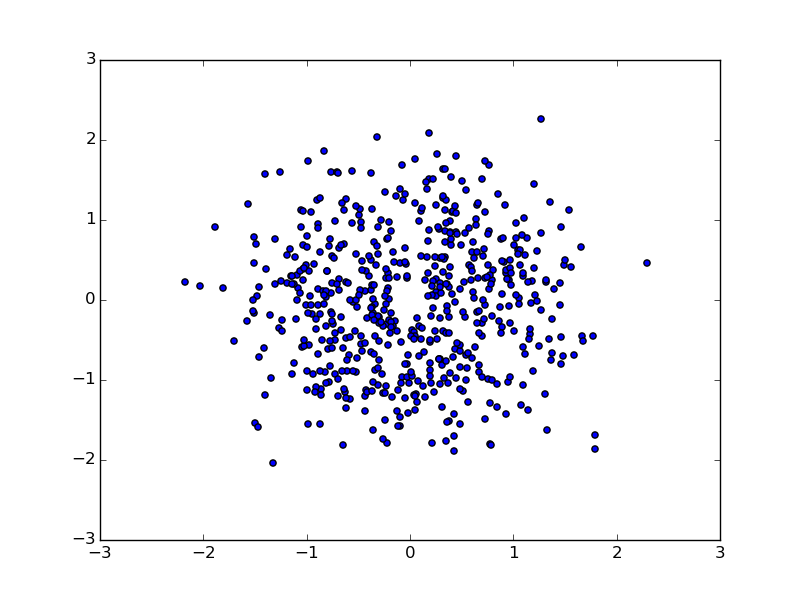
图5未经任何校正的星座点
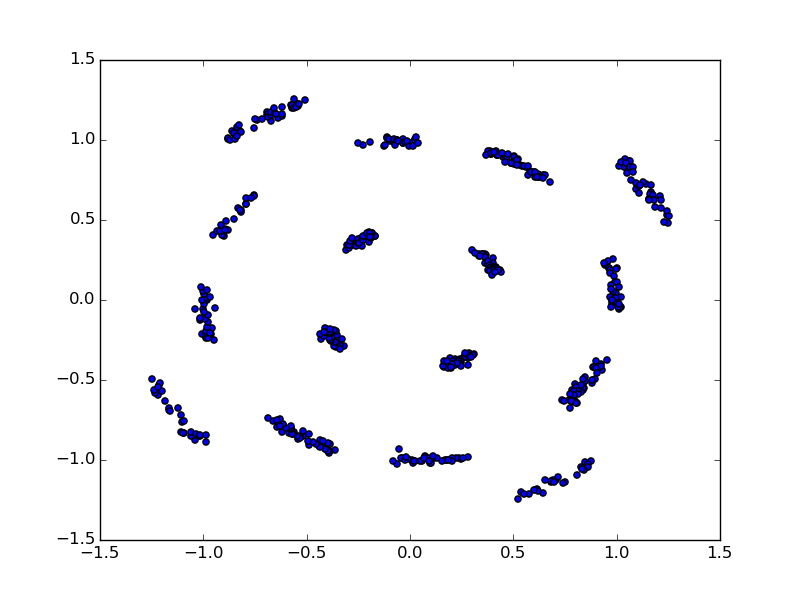
图 6仅粗略校正的星座点
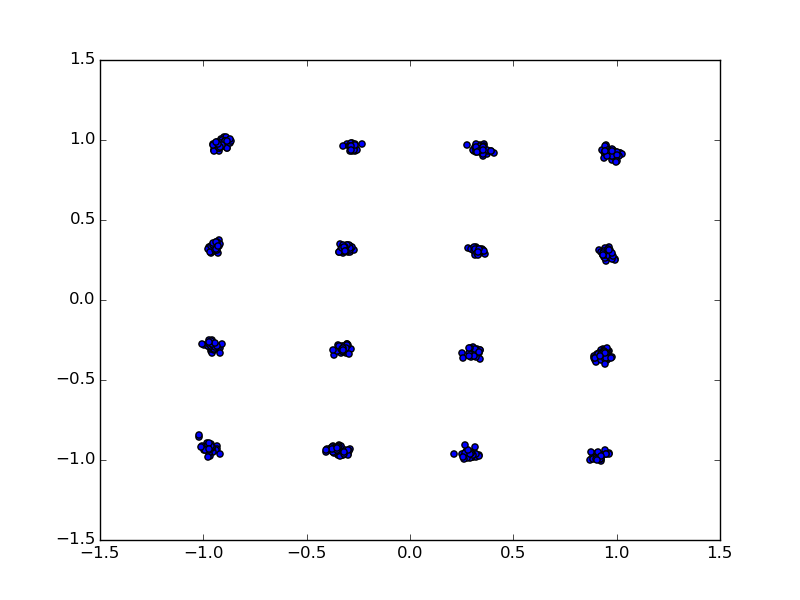
图7粗、精校正的星座点
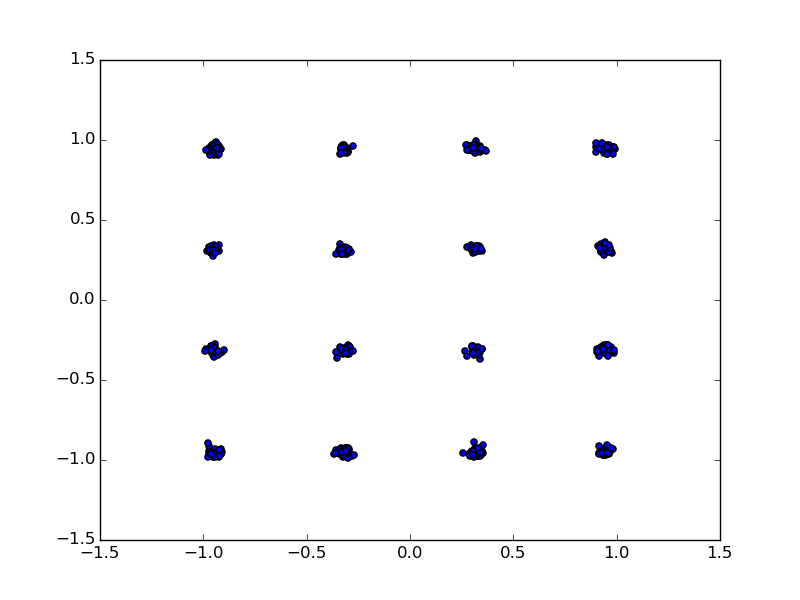
图 8粗校正、细校正和导频校正的星座点
图5至图8示出了16-QAM调制的802.11a数据包的星座点。这些图不是在这一步就能出来的,它只是展示了如果我做了这些校正,那么信号会在后面将样本映射到星座图上时会有哪些变化。
CFO 粗略修正
可以使用短前导码来估计粗略 CFO,如下所示:
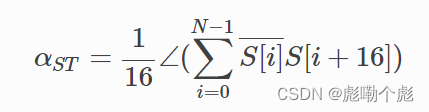
在这里∠ ( · )是复数的相位,N≤ 144 ( 160 − 16 )是所使用的短前导码的子集。直觉上,S[i] 和 S[i+16] 之间的相位差代表 16 个样本的累积 CFO。
得到αST之后,以下每个 I/Q 样本(从长前导码开始)均修正为:
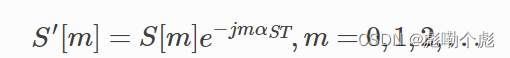
也就说我利用短前导码粗略地估计了这个相位偏移,并且通过计算出的值把从长前导码开始的后面的一切样本按照公式进行粗略的矫正。
sync_short模块中计算的,我们设置N= 64。图 4中的prod_avg被输入到 窗口大小设置为 64 的moving_avg模块中。
N要设置为短前导码长度的整数倍
CFO 精细修正
借助长前导码内的长训练序列,可以获得对 CFO 的更精细估计。
长前导码包含两个识别训练序列(每个 64 个样本,20 MSPS),相位偏移可以计算为:
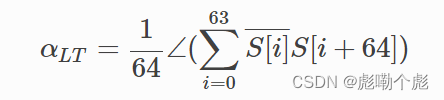
由于查找表中相位估计和旋转的分辨率有限,OpenOFDM 中省略了该步骤。
其实精细校正和前面的粗略校正是一个思路,先计算出相位的偏移,再将之后的样本全都按照公式修正。(精细校正借助的是长前导码,且校正公式同上)
总结:在这个章节分别借助短前导码和长前导码完成了CFO粗校正和CFO精校正,都是先计算出偏移的相位,再根据这个相位将后面的样本全部都修正,消除CFO的影响。
原文:Frequency Offset Correction — OpenOFDM 1.0 documentation

![LeetCode每日一题[C++]-310.最小高度树](https://img-blog.csdnimg.cn/direct/8ec62416e61f43539bf0e080ced67299.png)