1.概述

在逐层进行特征提取和空间转换的过程中,会损失大量信息,例如图中的马在建模过程中逐渐变得模糊,从而影响到最终的性能。YOLOv9尝试使用可编程梯度信息PGI解决这一问题。
具体来说, PGI包含三个部分,(1)主干分支(1)辅助可逆分支。(2)多级辅助信息。其核心思想通俗来说,就是通过引入辅助梯度分支计算损失和梯度,从而降低信息逐层建模中的损失。需要说明的是,辅助梯度分支只在训练中参与计算损失,而不在推理中使用。
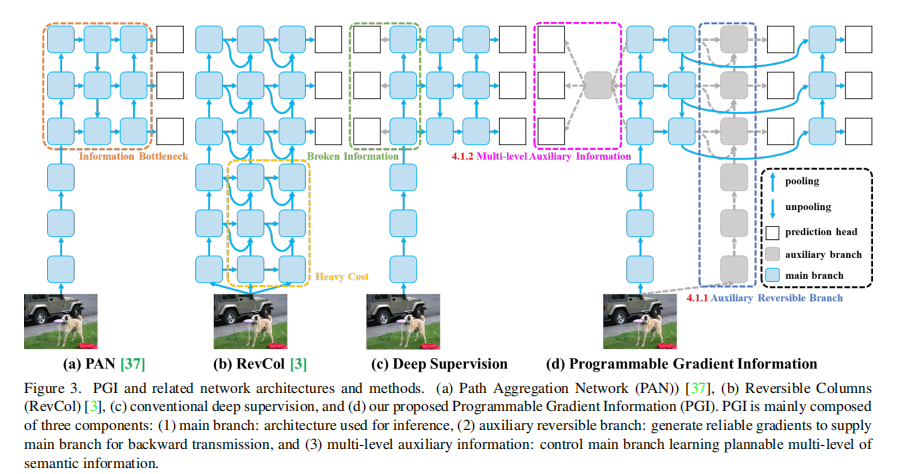
2. 主干分支
主干分支即yolo系列的PANet.
3.辅助可逆分支
辅助可逆分支提供了一种监督机制,能够提供梯度信息,保证主分支信息建模的正确性和有效性。此外,由于可逆分支只在训练中使用,能够有效保证推理时间。
4.多级辅助信息
在进行目标检测的过程中,我们往往会使用特征金字塔。引入辅助可逆分支后,80*80尺度的浅层特征可能会受到引导,学习小物体检测所需的特征,此时系统将其他大小的物体的位置视为背景。然而,上述行为会导致深层特征金字塔丢失预测目标对象所需的大量信息。多级辅助分支,就是告诉三层特征,“你们都需要接收到所有关于目标对象的信息,不管是小目标、中目标和大目标”。
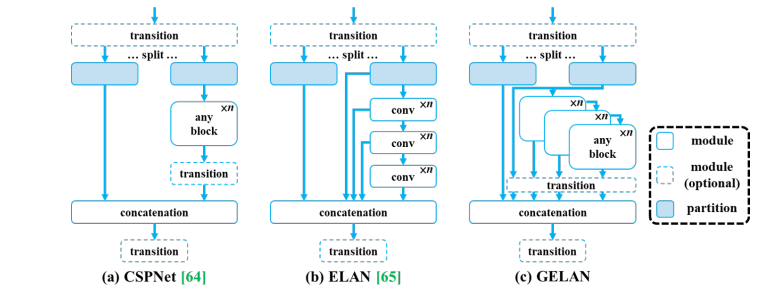
5.Generalized ELAN
YOLOv9也对yolov7的特征提取模块进行了优化,其核心思想还是yolo一直以来的csp思想,这方面与yolov8完全一致。
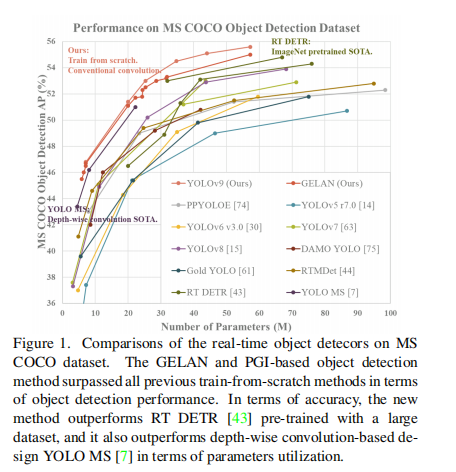
6.消融实验
首先,作者对YOLOv9的特征提取模块进行了消融实验,当然是YOLO系列的CSP模块表现得更好。
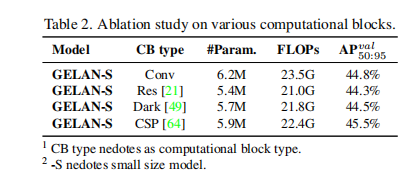
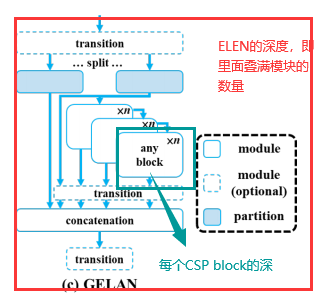
然后作者对GELEN的深度和CSP模块的深度做了消融,发现网络对这方面的参数不敏感。
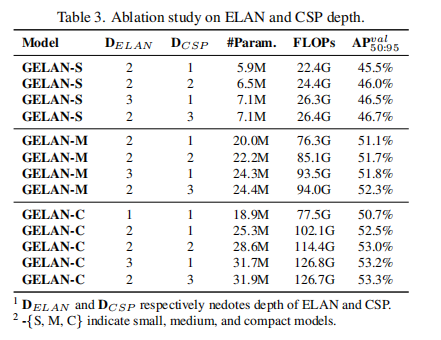
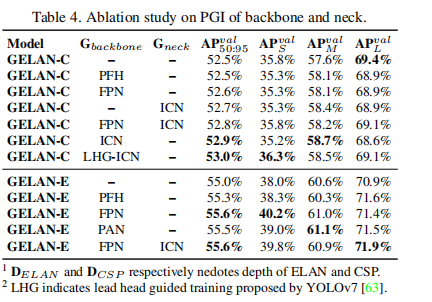
以及PGI在backbone和neck的设置
![LeetCode每日一题[C++]-310.最小高度树](https://img-blog.csdnimg.cn/direct/8ec62416e61f43539bf0e080ced67299.png)