【数据结构和算法初阶(C语言)】队列实操（概念实现+oj题目栈和队列的双向实现以及循环链表难点题目详解！）

目录

1. 队列的概念及结构

2.队列结构存在的意义应用

3.队列实现的结构选择

4.队列实现

5.队列对数据的处理

5.1队列初始化

5.2队尾入数据

5.3队头出数据

5.4获取队列尾部元素

5.5获取队列头部元素

5.6获取队列中元素个数

5.7检测队列是否为空

5.8销毁队列

6.循环队列补充

7.使用队列实现栈

8.使用栈实现队列

9.实现循环队列

编辑

10.结语

1. 队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，

队列具有先进先出 FIFO(First In First Out)

入队列：进行插入操作的一端称为队尾

出队列：进行删除操作的一端称为队头

2.队列结构存在的意义应用

①公平排队（决定公平性的东西）

不会出现插队问题（不过有竞争问题，两个窗口同时叫或者两个号码一起出---操作系统加速解决）

比如医院或者银行的排号---抽号机

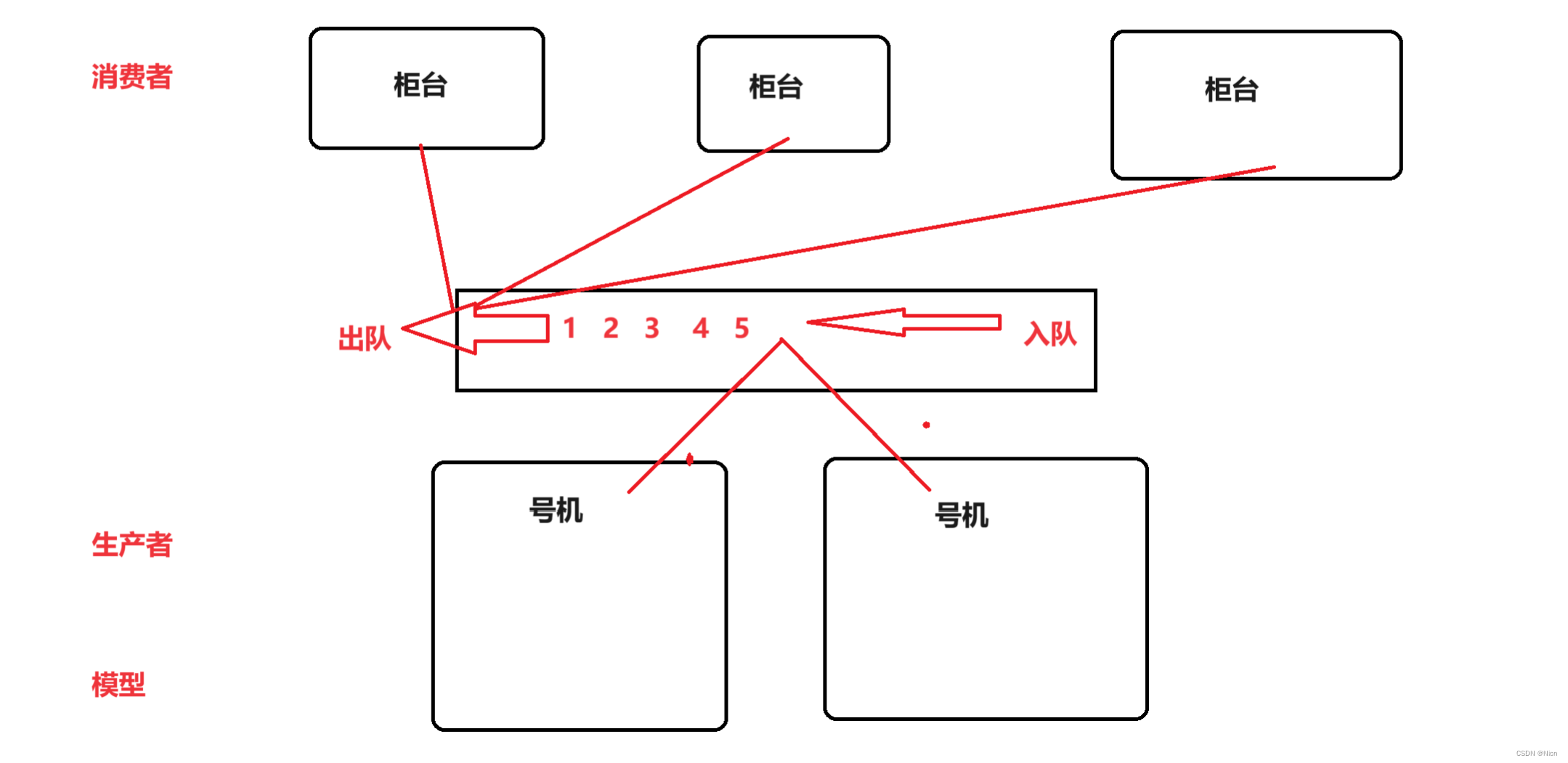
②BFS广度优先

树，迷宫实现等

3.队列实现的结构选择

数组和链表都可以实现队列，但是链表的头插尾插，头删尾删要方便些，所以首选链表

单向还是双向：选择单向，双向的优势是方便找前一个1节点，没有这个需求。（找尾不是因为双向，双向循环方便找尾，但是单向加一个尾巴指针也可以解决）

是否需要带哨兵位的链表：哨兵位是为了解决二级指针（可以将头尾指针封装为结构体进行传参，这样就可以改变真实的指针了，所以哨兵位可要可不要），尾插少一次判断。

选择单向不循环链表即可实现。

4.队列实现

typedef  int QdataType;


typedef struct QListNode
{
	struct QListNode* next;
	QdataType data;
}QNode;

//将头尾指针封装为一个结构体，解决传递二级指针的问题

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;//保存链表的大小
}Queue;

5.队列对数据的处理

5.1队列初始化

void QUeueInit(Queue* pq)//初始化队列
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

5.2队尾入数据

void QueuePush(Queue* pq, QdataType x)//队列增加数据
{
	assert(pq);//首先传入的这个结构体要存在
	//申请到节点来创建
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
	}
	//新节点初始化
	newnode->data = x;
	newnode->next = NULL;
	//准备插入，看一下是不是第一次插入
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
		pq->size++;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = pq->tail->next;
		pq->size++;
	}
}

5.3队头出数据

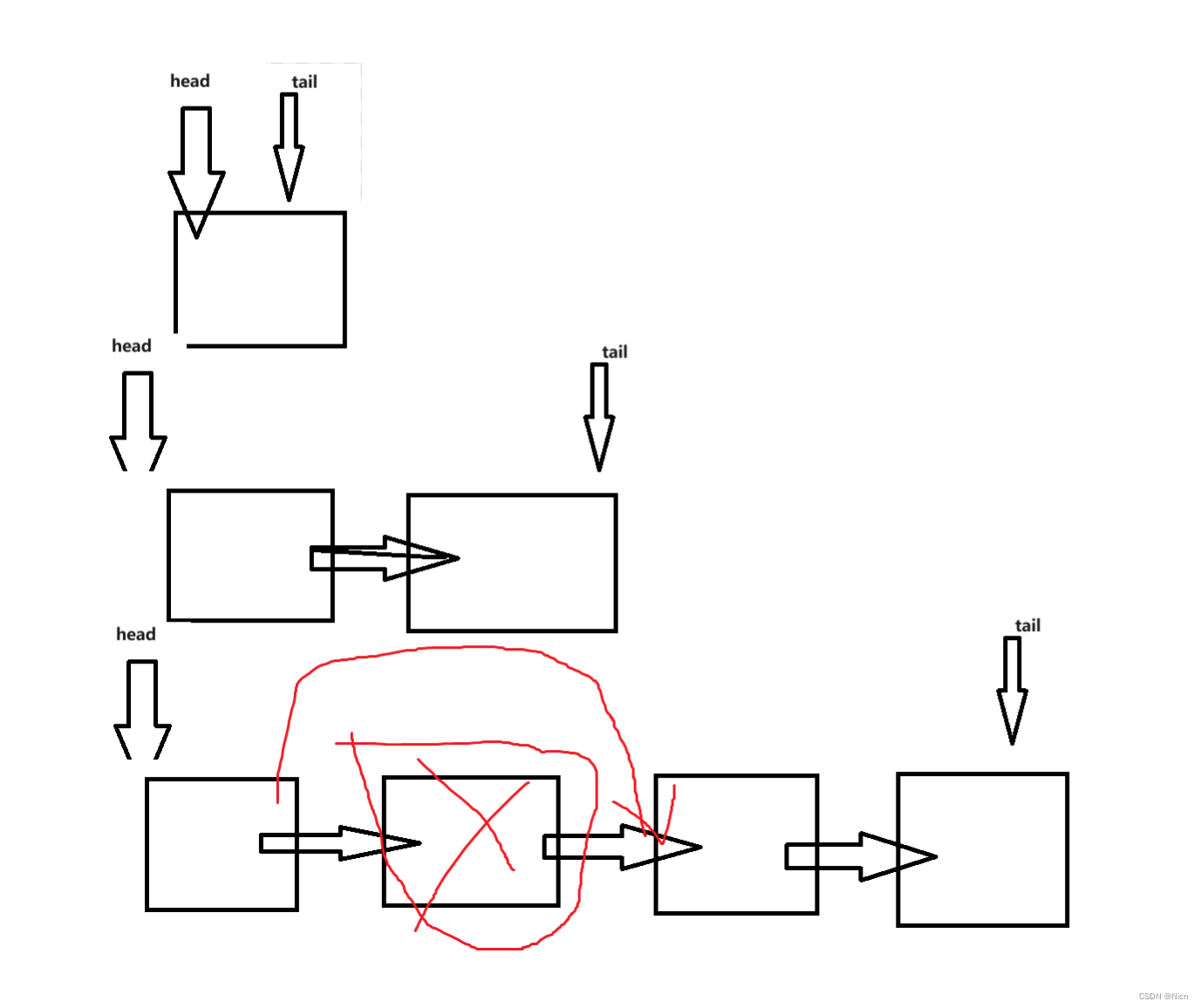
void QueuepPop(Queue* pq, QdataType x)//队列删除元素
{
	assert(pq);
	assert(pq->size != 0);
	if (pq->head->next == NULL)//因为不是带哨兵位的，删除到最后一个位置防止尾指针成为野指针，单独处理
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
		pq->size--;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
		pq->size--;
	}
	
}

5.4获取队列尾部元素

QdataType QueueBack(Queue* pq)//获取队列前后面元素
{
	assert(pq);
	assert(!QueueEmpty);
	return pq->tail->data;
}

5.5获取队列头部元素

QdataType QueueFront(Queue* pq)//获取队列前面元素
{
	assert(pq);
	assert(!QueueEmpty);
	return pq->head->data;
}

5.6获取队列中元素个数

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

5.7检测队列是否为空

bool QueueEmpty(Queue* pq)//检测队列是否为空
{
	assert(pq);
	return pq->head == NULL;
}

5.8销毁队列

void QueueDestory(Queue* pq)//销毁队列
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = cur->next;
	}
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

6.循环队列补充

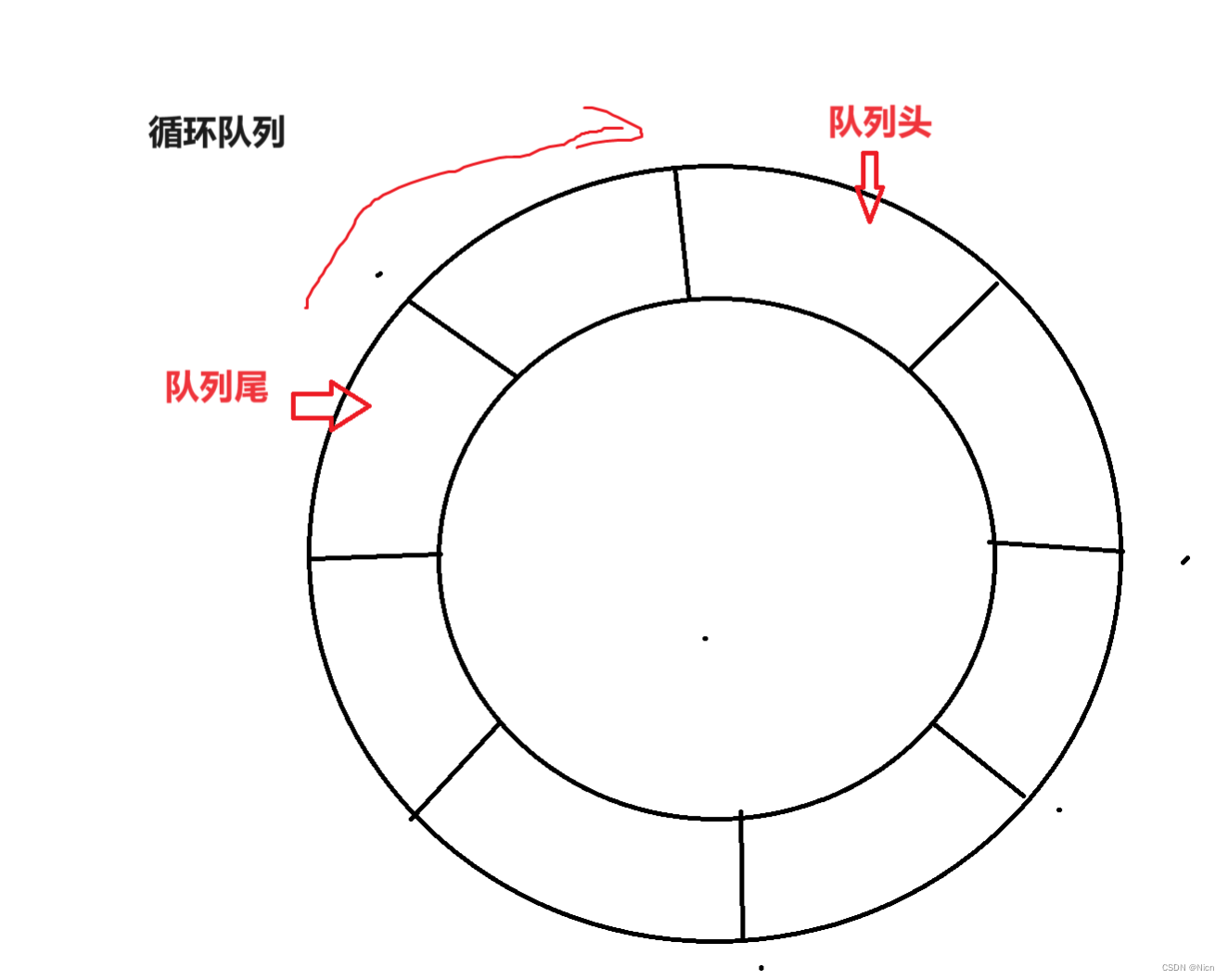
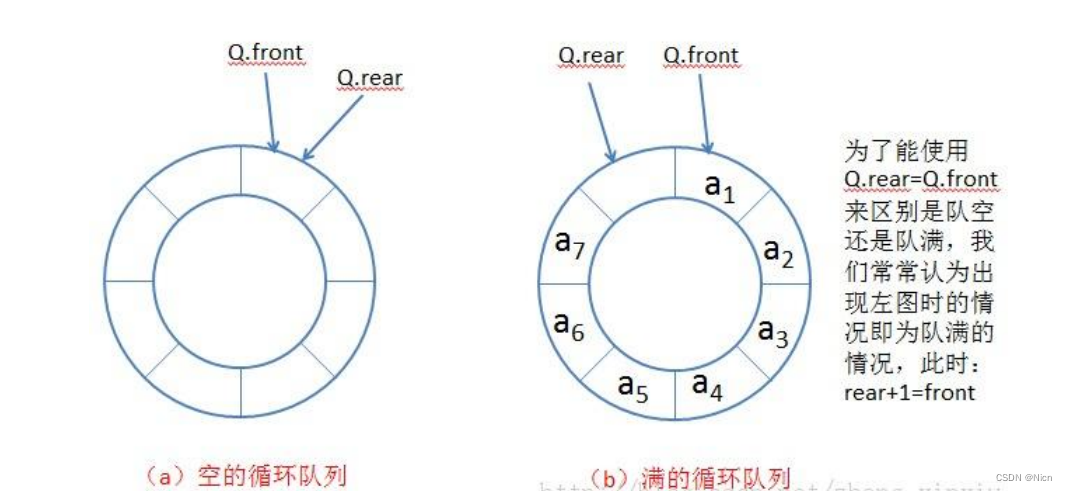
设计你的循环队列实现。循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

7.使用队列实现栈

链接跳转题目：

. - 力扣（LeetCode）. - 备战技术面试？力扣提供海量技术面试资源，帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/implement-stack-using-queues/

分析：栈的结构特点是数据先进后出

队列的结构特点是先进先出

那么就是说我们需要使用先进先出的结构来实现后进先出的结构：

这是初始状态：

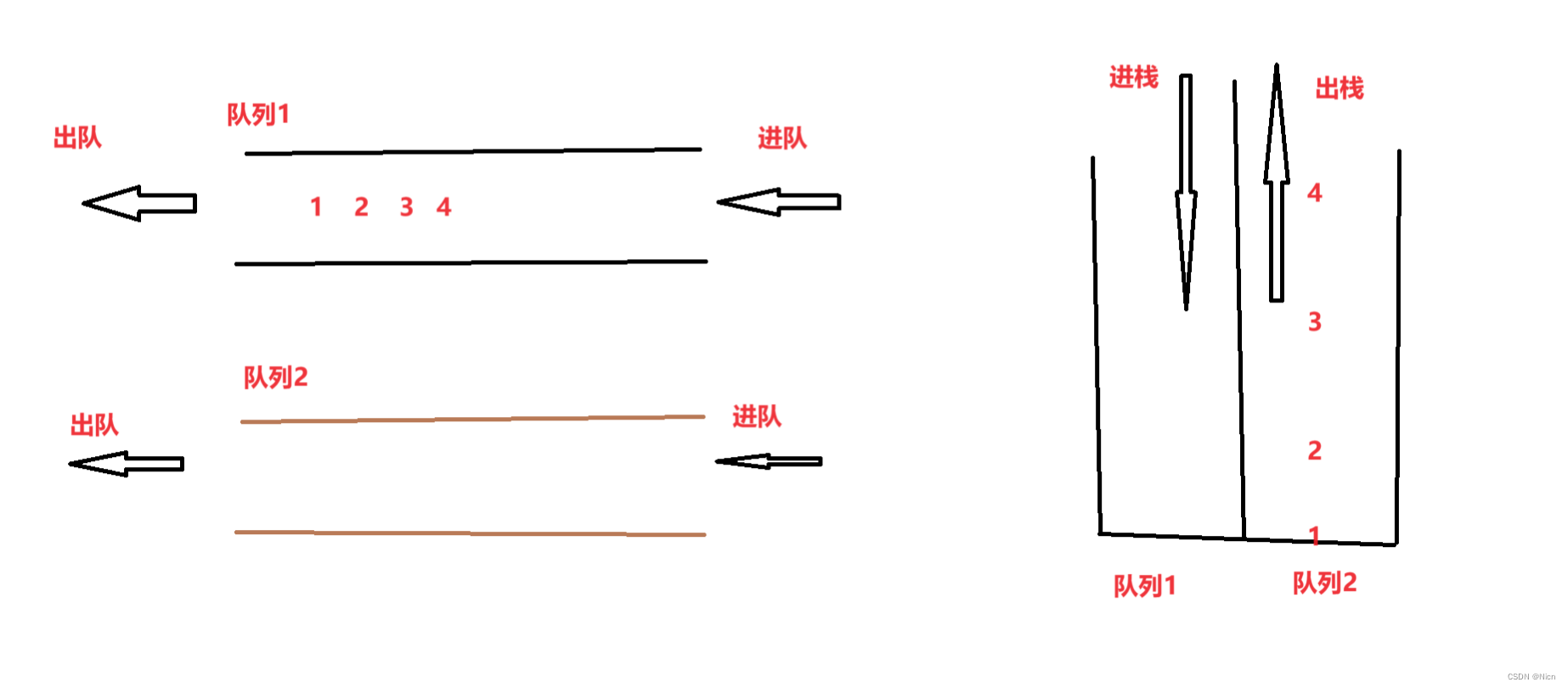
对于队列来说先出1，对于栈来说先出4，我们现在就是要想办法利用队列的函数实现我们的先出4：

我们先出123将其放进队列2，然后单独删除4是不是就实现了后进先出。

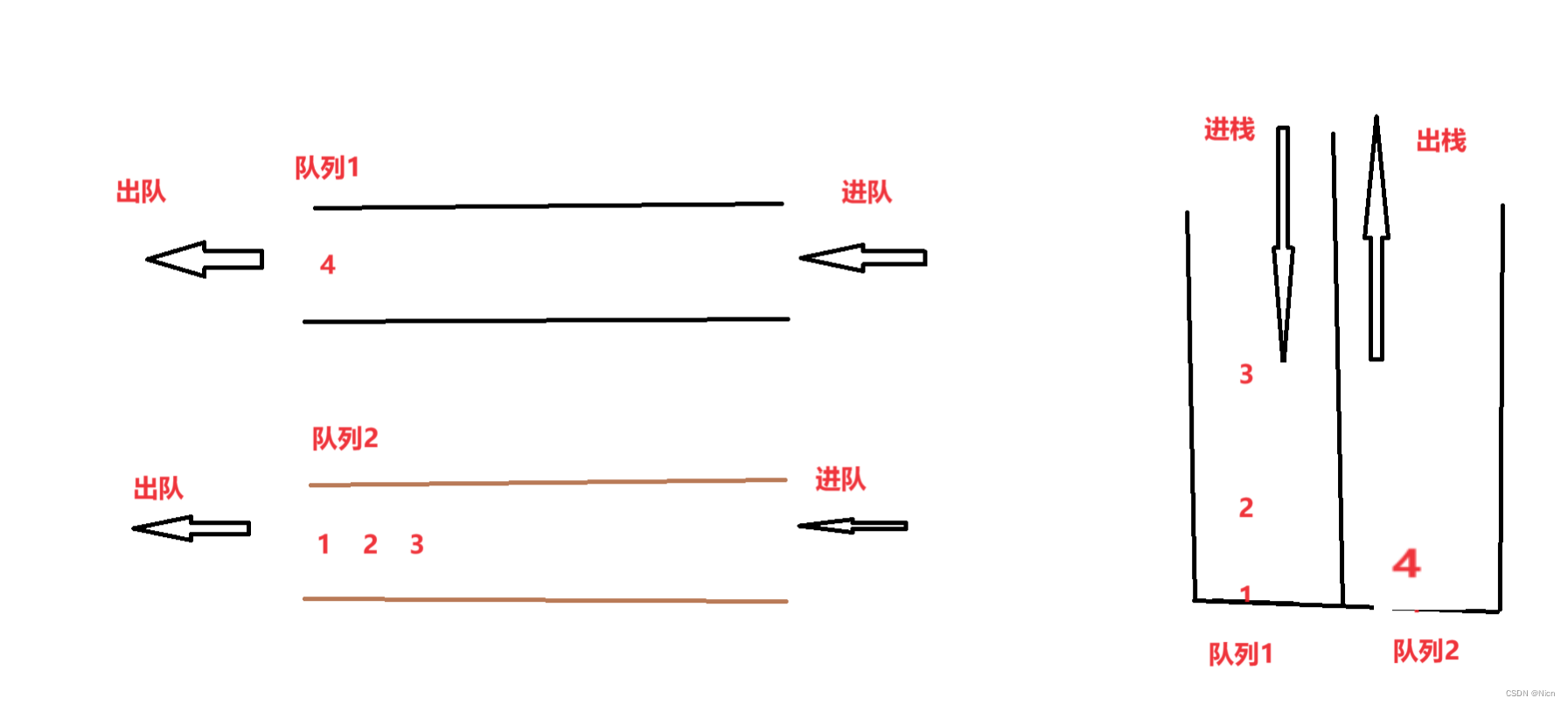
那么后续有新数据要进入我们自己的“栈”直接进入有元素的队列尾进就好了，然后一样的办法进行出栈。如果两个队列都没有元素，数据放入那个队列都可以

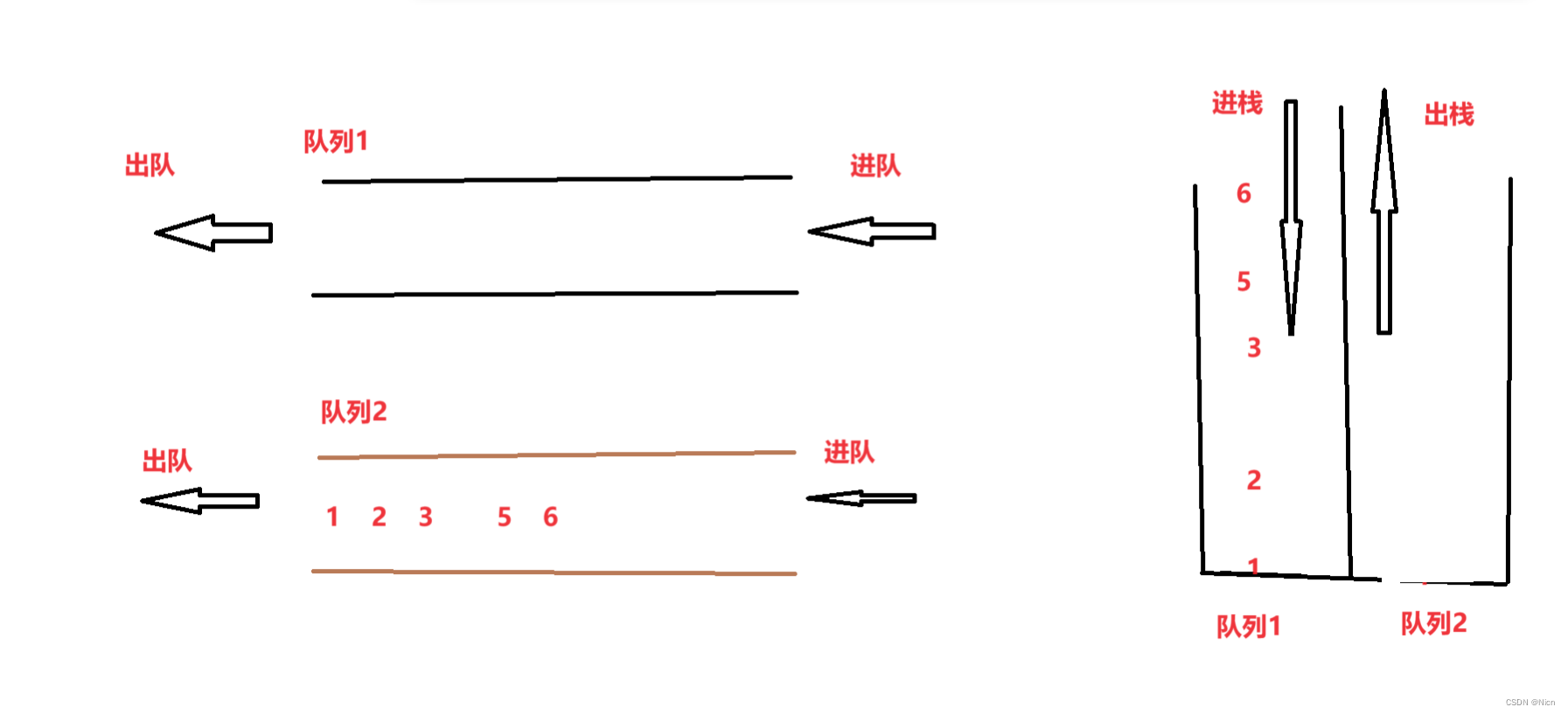出栈：

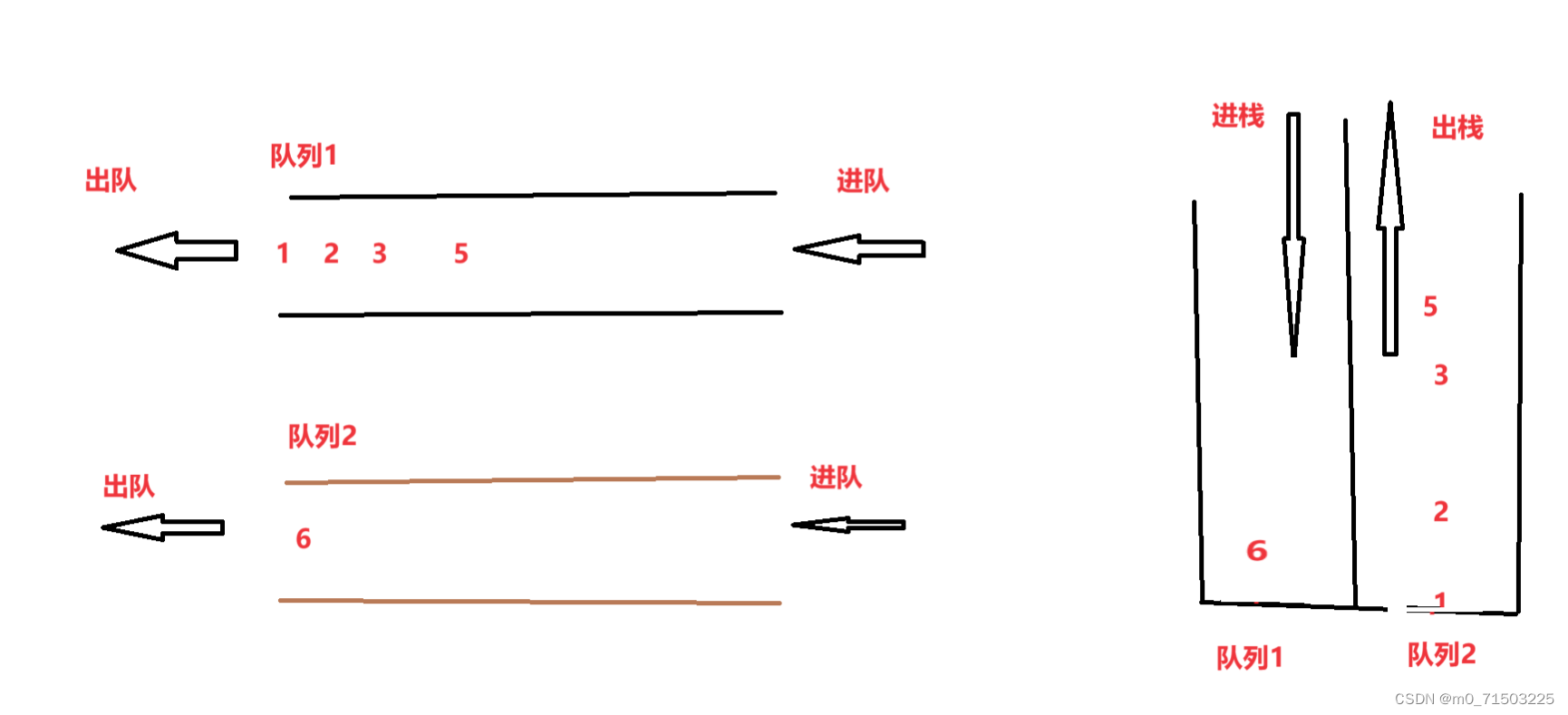
过程清楚我们来上代码：主逻辑代码：

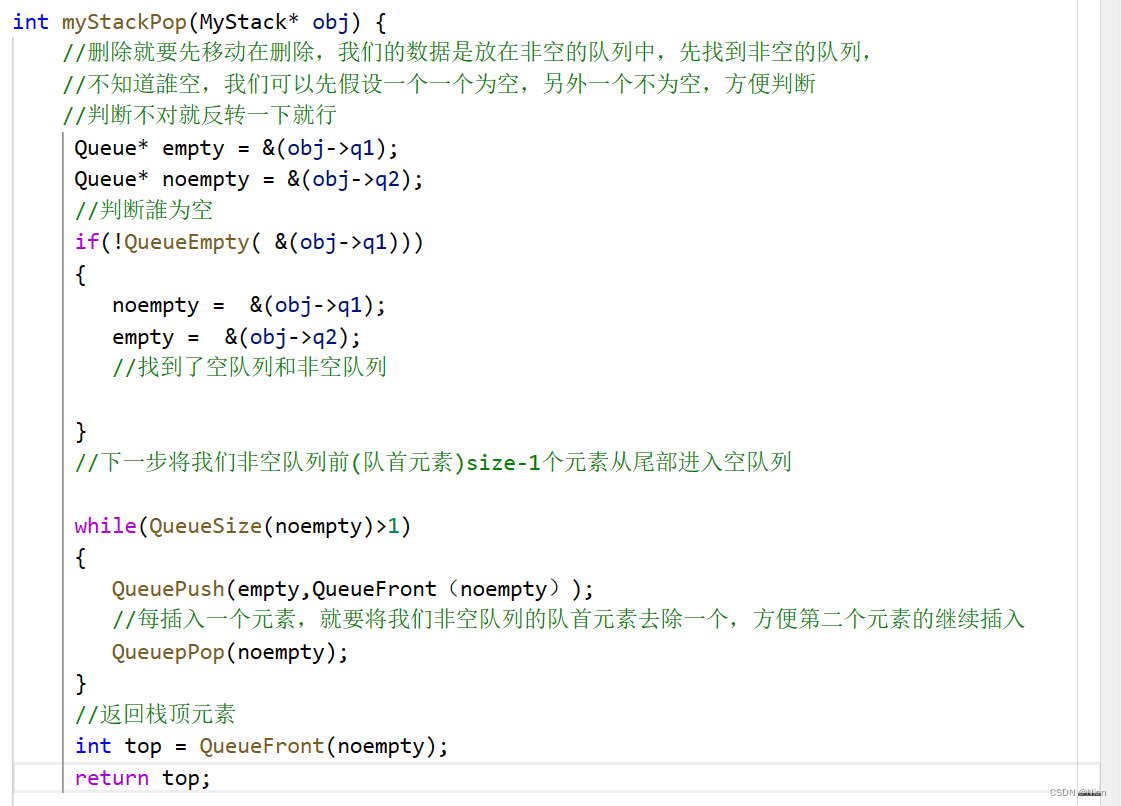
结构图：

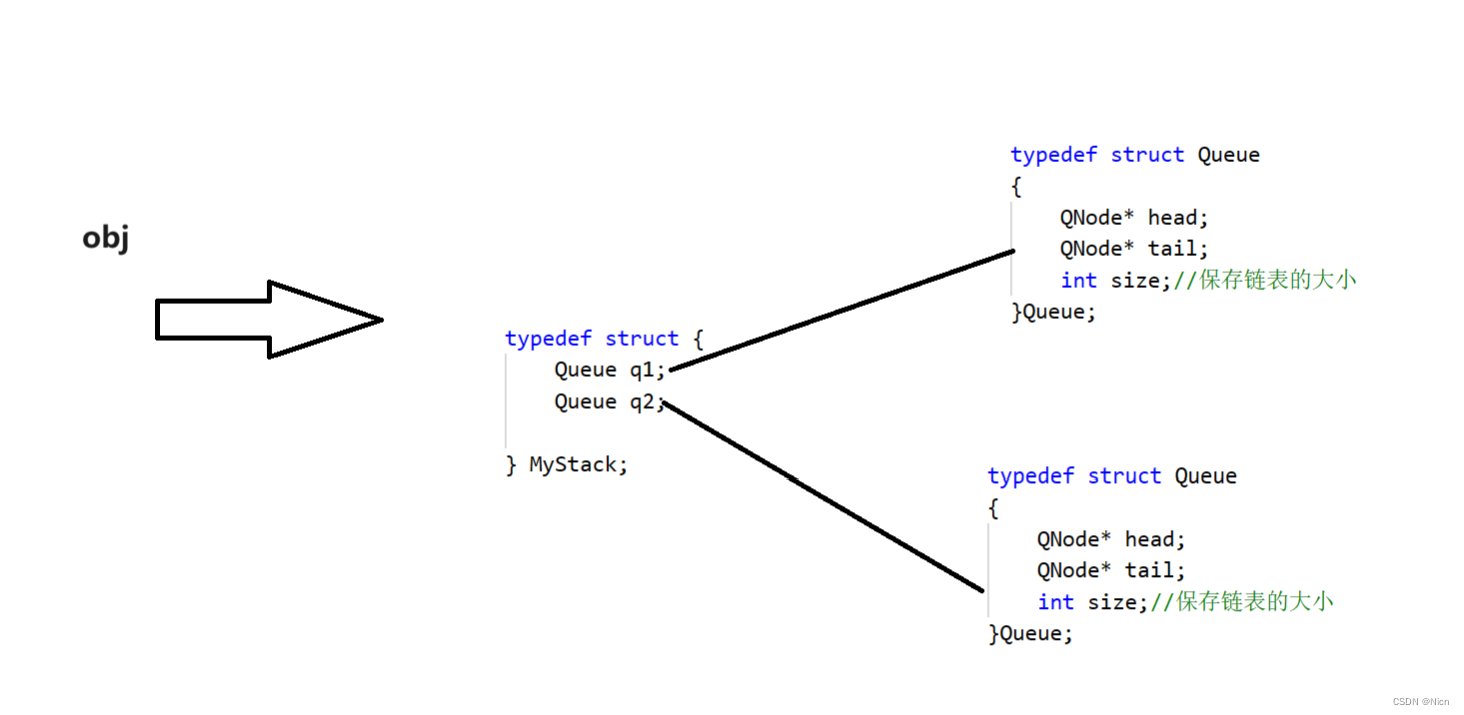
8.使用栈实现队列

做题地址

原理：一个栈作为数据进入，另外一个栈作为数据流出

. - 力扣（LeetCode）

队列是先进先出，栈是先进后出：

这是初始状态

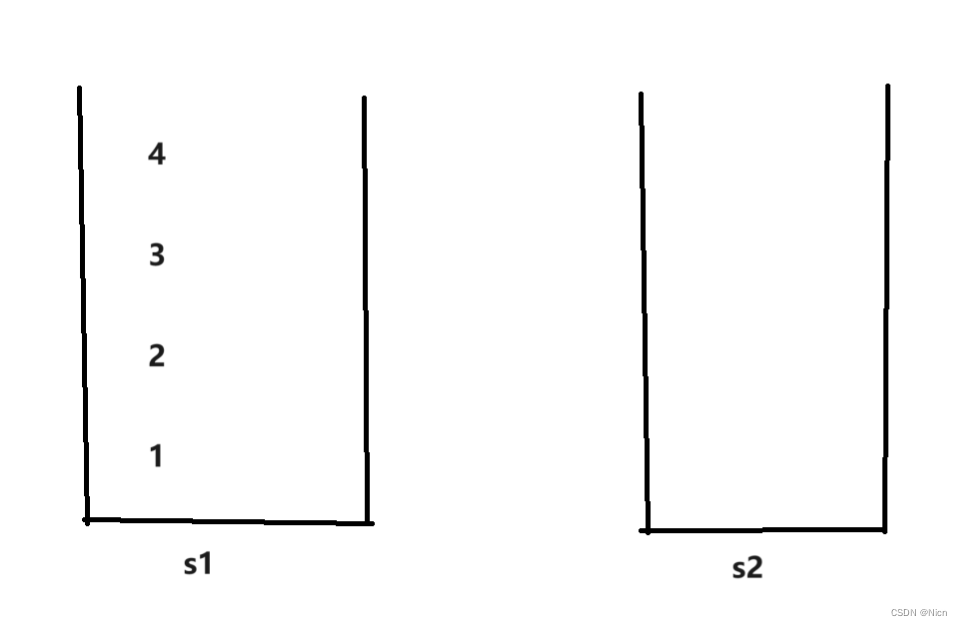
如果是队列1那么出数据的顺序就是1.2.3.4

栈的出数据顺序是4.3.2.1

我们的思路是：将数据出到栈2，然后从栈顶出数据就可以实现一次数据的顺序改变

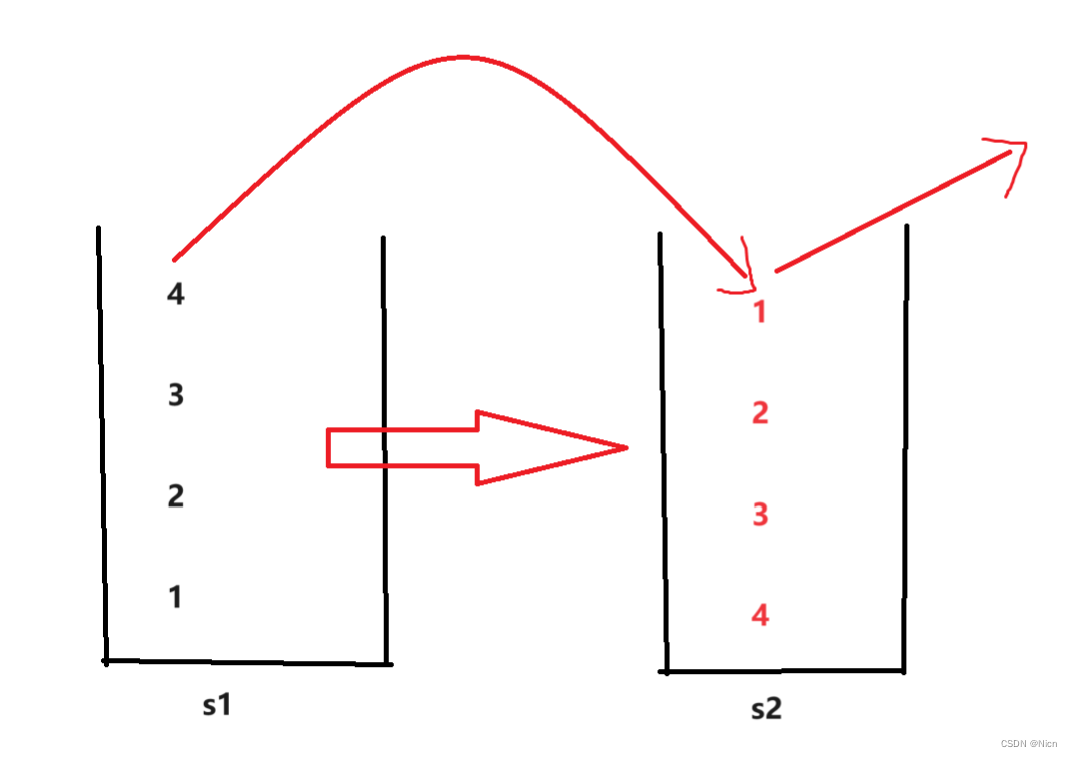
当后续插入数据的时候：我们应该往空的栈里面去插入数据，一直到我们的这个非空栈数据出完了在进行数据移值：

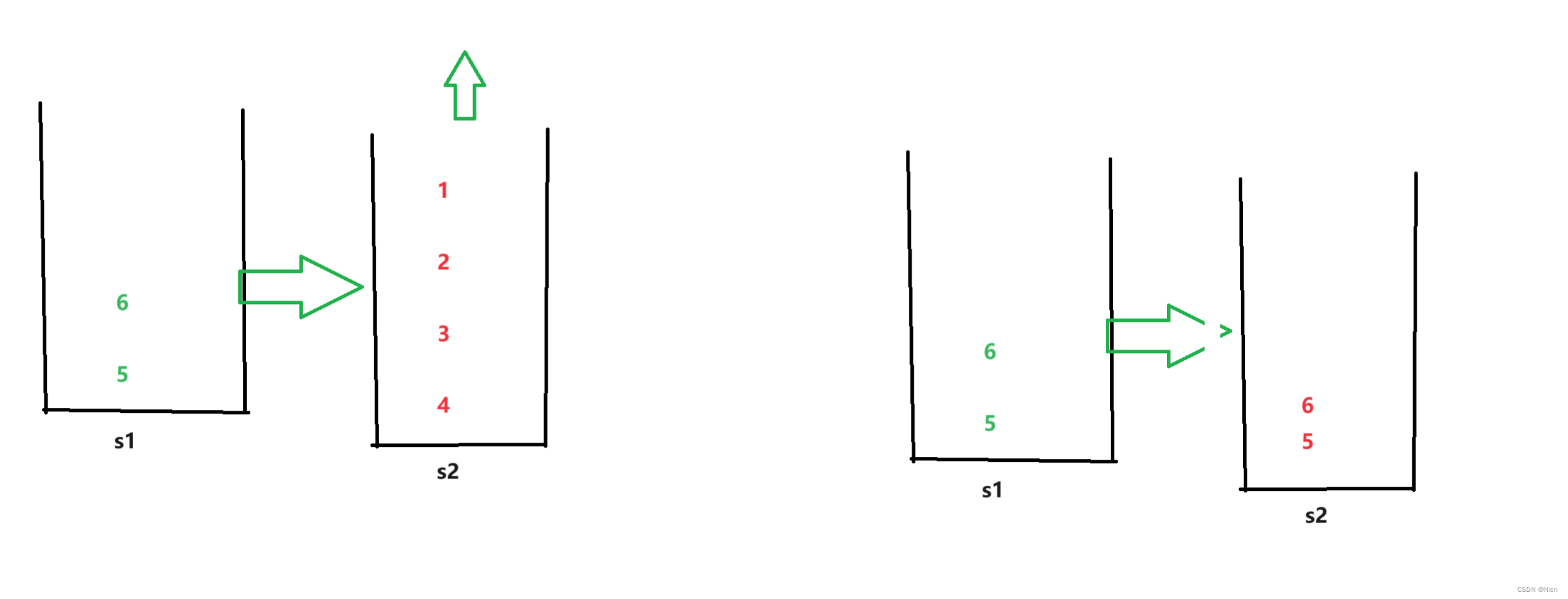
实现原理明白了；动手写代码实现

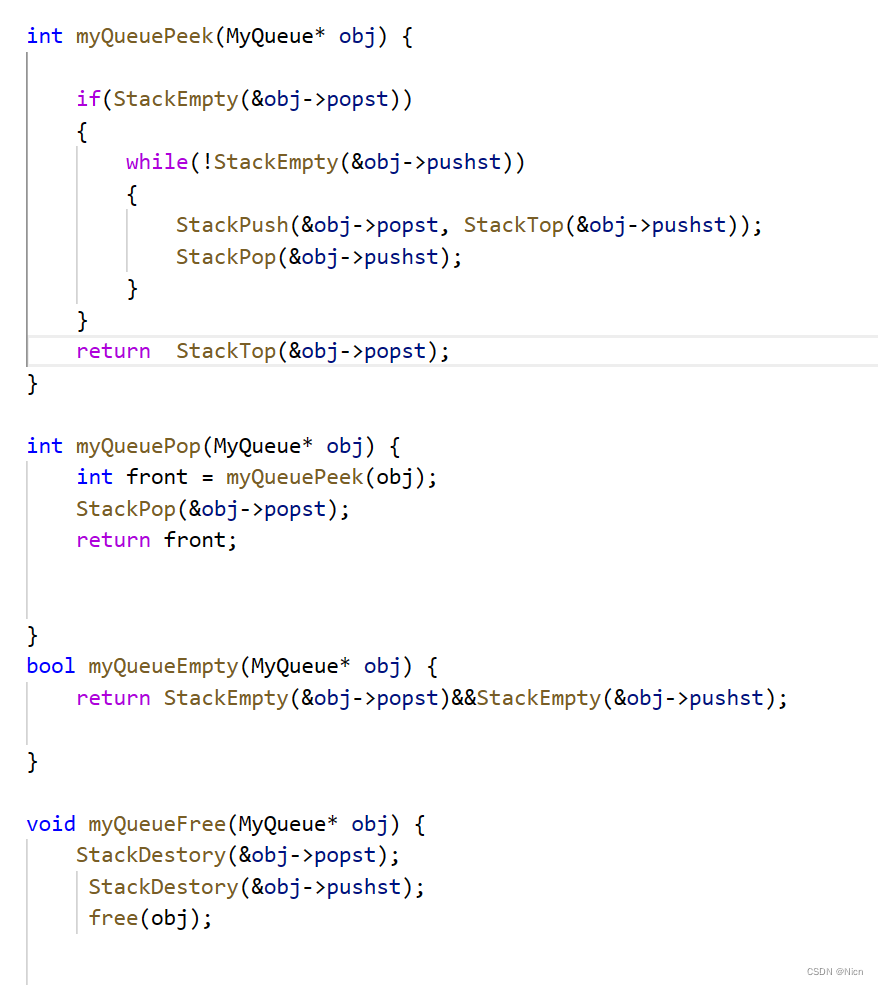
结构图：

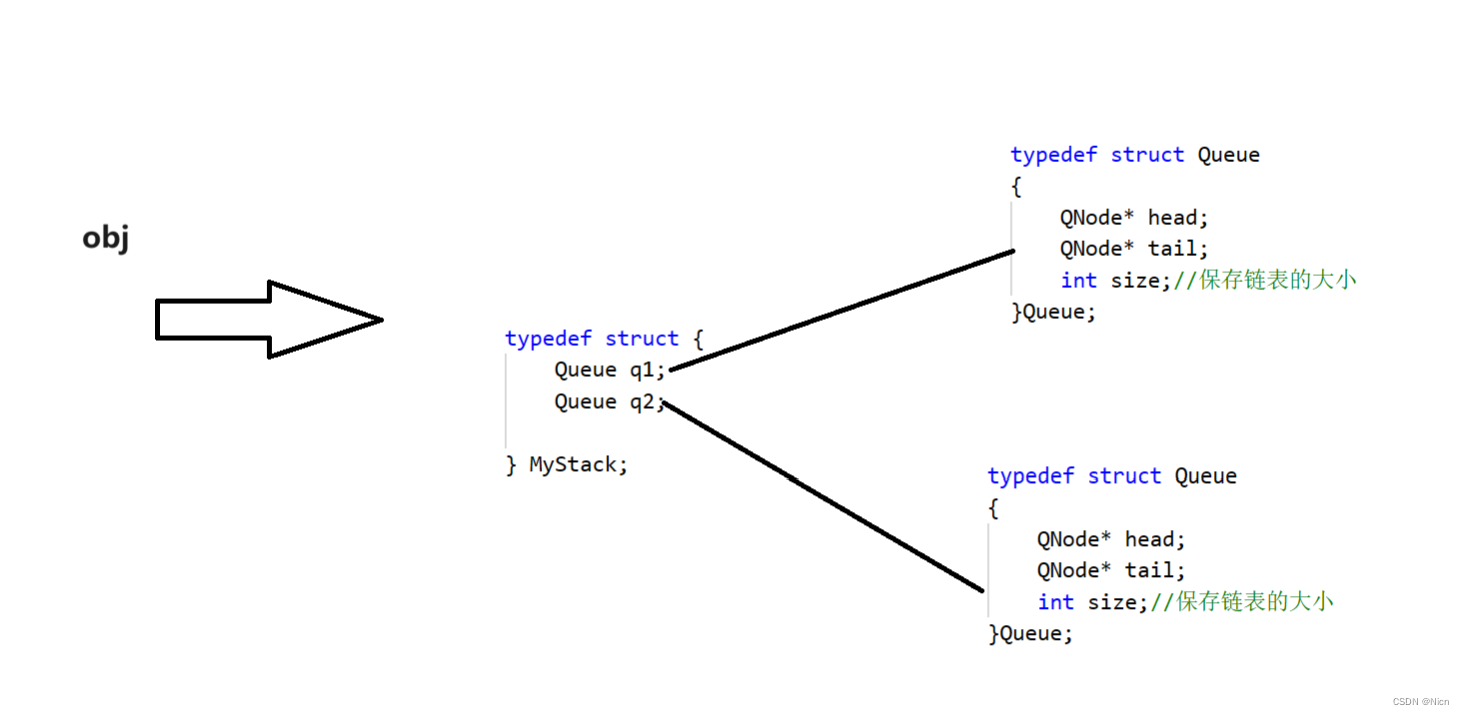
9.实现循环队列

首先分析链表实现这个循环列表的难易程度：

首先考虑单向链表，带头尾指针：

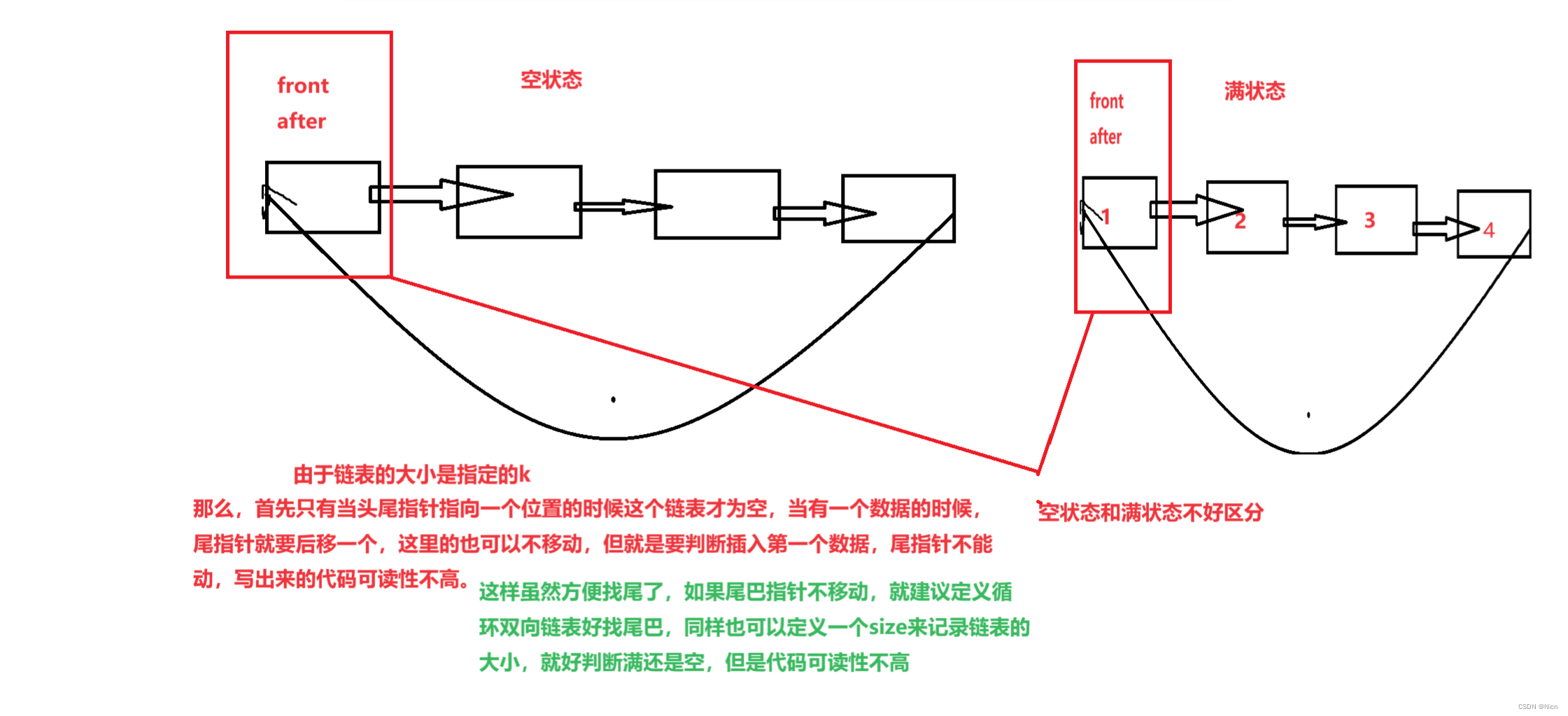
链表是可以实行的，不过一开始就要创建一个循环链表还是有些麻烦，

介绍巧解决方案：使用数组多开一个空间法：

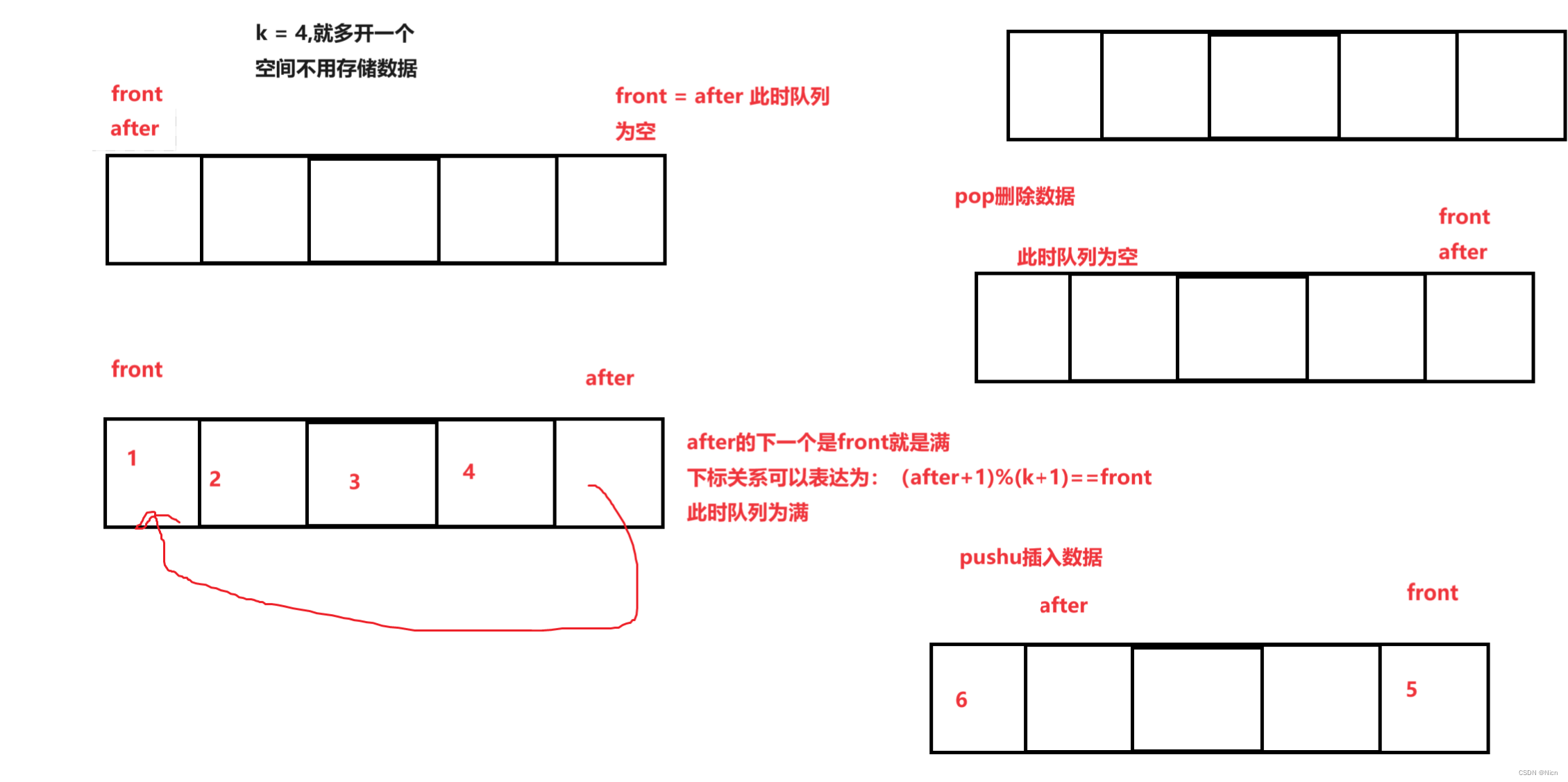
数组麻烦的地方就是回绕的时候要多判断一次。

用数组实现，

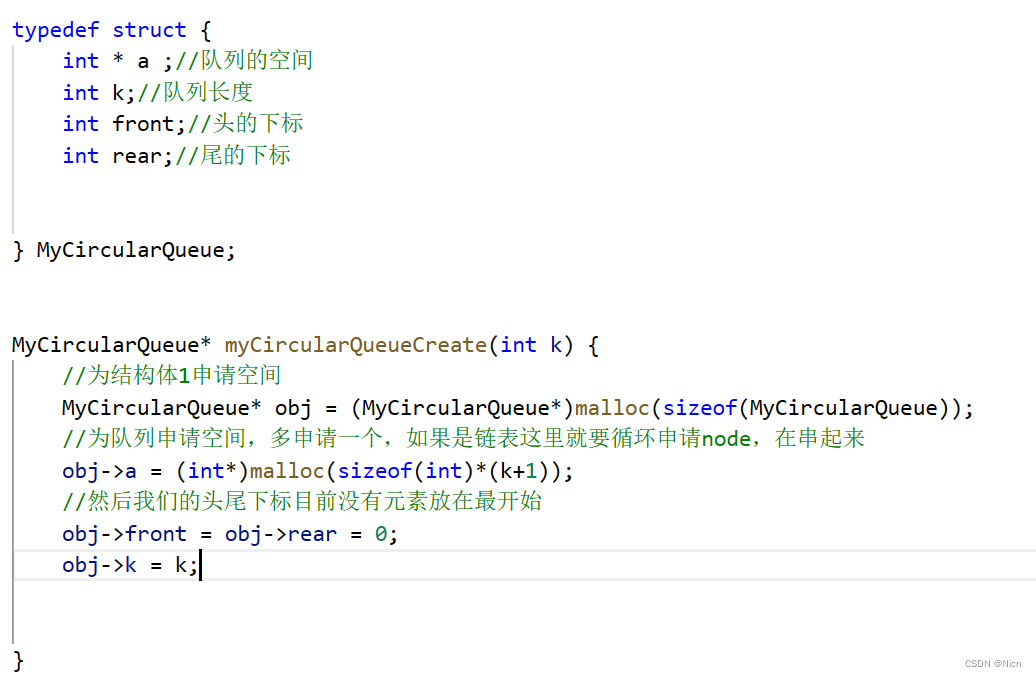
判满和判空

插入数据前要先判断满没满

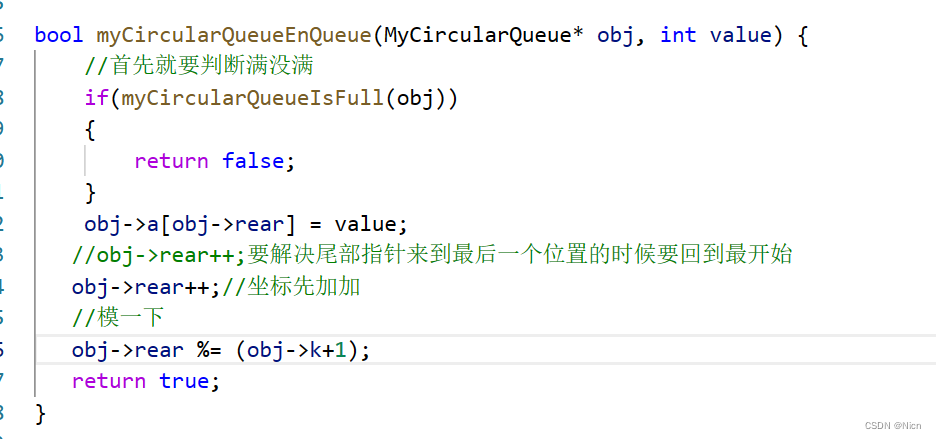
特别注意就是尾指针在最后的情况，统一模当然也可以担当rear = K+1的时候，直接置0.

删除数据前要判断空不空

取出头数据，先判空

取尾数据

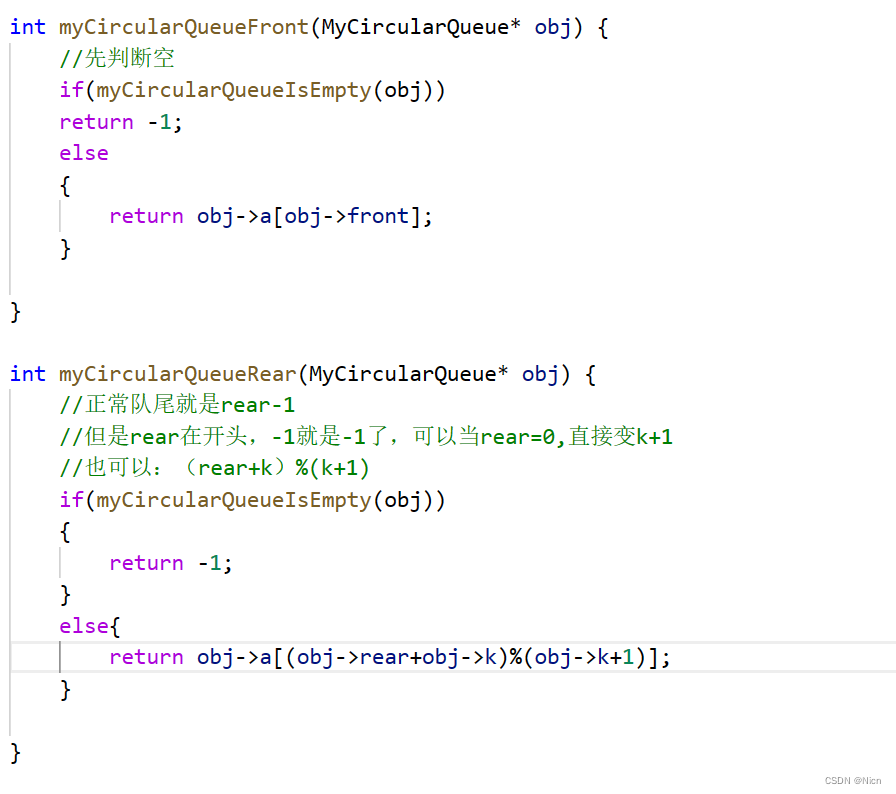
通过；附上源代码

typedef struct {
    int * a ;//队列的空间
    int k;//队列长度
    int front;//头的下标
    int rear;//尾的下标

    
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    //为结构体1申请空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    //为队列申请空间，多申请一个，如果是链表这里就要循环申请node，在串起来
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    //然后我们的头尾下标目前没有元素放在最开始
    obj->front = obj->rear = 0;
    obj->k = k;
    return obj;

    
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    //我们的rear尾指针和头指针相等的时候就满
    return obj->front == obj->rear;
    
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    //当尾巴指针的下一个，这里由于是数组，是通过下标确定，所以是下标之间的关系要重叠起来
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    //首先就要判断满没满
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->rear] = value;
   //obj->rear++;要解决尾部指针来到最后一个位置的时候要回到最开始
   obj->rear++;//坐标先加加
   //模一下
   obj->rear %= (obj->k+1);
   return true;
}




bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    //首先要判断空不空

    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    //让后删除一个，是从头删除，那么头指针就要往后走一下，然后也要注意绕回来的问题
    //不用抹除数据，之间角标加加，到时候插入数据，值会覆盖掉
    obj->front++;
    obj->front %= (obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    //先判断空
    if(myCircularQueueIsEmpty(obj))
    return -1;
    else
    {
        return obj->a[obj->front];
    }
    
}

int myCircularQueueRear(MyCircularQueue* obj) {
    //正常队尾就是rear-1
    //但是rear在开头，-1就是-1了，可以当rear=0,直接变k+1
    //也可以：（rear+k）%(k+1)  
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else{
        return obj->a[(obj->rear+obj->k)%(obj->k+1)];
    }
    
}



void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
    
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/