【机器学习-02】矩阵基础运算---numpy操作

news2024/11/24 16:34:52

  在机器学习-01中，我们介绍了关于机器学习的一般建模流程，并且在基本没有数学公式和代码的情况下，简单介绍了关于线性回归的一般实现形式。不过这只是在初学阶段、为了不增加基础概念理解难度所采取的方法，但所有的技术最终都是为了解决实际问题的，因此，接下来，我们就在之前的基础上更进一步，从一个更加严谨的理论体系出发、来尝试进行一种更加贴合实际应用所采用的一般方法的建模方法的学习。

import numpy as np
import pandas as pd

一、NumPy矩阵运算基础

  在进入到本节正式内容之前，我们需要先补充一些矩阵相关基础概念，以及矩阵运算的基本方法。
  在机器学习基础阶段，需要掌握的矩阵及线性代数基本理论包括：

  • 矩阵的形变及特殊矩阵的构造方法：包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等；
  • 矩阵的基本运算：包括矩阵乘法、向量内积、矩阵和向量的乘法等；
  • 矩阵的线性代数运算：包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等；
  • 矩阵分解运算：特征分解、奇异值分解和SVD分解等。
    本节将先介绍前三部分内容，矩阵分解部分内容将在后续补充。

1.NumPy中的矩阵表示

  在NumPy中，二维数组(array)和matrix类型对象都可以用于表示矩阵，并且也都具备矩阵的代数学方法。

  • 利用数组创建矩阵
A = np.array([[1, 2], [1, 1]])

A

array([[1, 2],
       [1, 1]])

type(A)

numpy.ndarray
  • 利用mat创建矩阵
AM = np.mat(A)
AM

matrix([[1, 2],
        [1, 1]])
        
type(AM)
numpy.matrix

关于两种对象类型的选取，此处进行简单说明：

  • NumPy中的matrix类型对象和MATLAB中的matrix类型等价，和NumPy中数组类型对象底层基本结构不同；
  • 在NumPy中，针对大规模数据，数组类型对象的计算速度要快于矩阵类型对象；
  • 矩阵类型对象可以通过运算符直接进行矩阵乘法，而二维数组要进行矩阵乘法（及其他矩阵运算），则必须要使用包括linalg（线性代数运算）模块在内的相关函数。
AM * AM

matrix([[3, 4],
        [2, 3]])

A.dot(A)
array([[3, 4],
       [2, 3]])

# 新版NumPy也支持使用符号进行矩阵乘法
A @ A
array([[3, 4],
       [2, 3]])

为了执行更高效的计算、以及确保代码整体基本对象类型统一，课程如无说明，将统一使用二维数组表示矩阵。

2.NumPy中特殊矩阵构造方法

  在实际线性代数运算过程中，经常涉及一些特殊矩阵，如单位矩阵、对角矩阵等，相关创建方法如下：

函数描述
a.T数组a转置
np.eye(n)创建包含n个分量的单位矩阵
np.diag(a1)以a1中各元素，创建对角矩阵
np.triu(a)取矩阵a中的上三角矩阵
np.tril(a)取矩阵a中的下三角矩阵

下面将展示一些矩阵的基本操作：

# 创建一个2*3的矩阵
a1 = np.arange(1, 7).reshape(2, 3)

a1
array([[1, 2, 3],
       [4, 5, 6]])

# 转置
a1.T

array([[1, 4],
       [2, 5],
       [3, 6]])

矩阵的转置就是每个元素行列位置互换

# 创建单位矩阵
np.eye(3)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

单位矩阵之所以被称为“单位”，核心原因在于单位矩阵和任何矩阵相乘，都将返回原矩阵。

a = np.arange(5)

a
array([0, 1, 2, 3, 4])

np.diag(a)
array([[0, 0, 0, 0, 0],
       [0, 1, 0, 0, 0],
       [0, 0, 2, 0, 0],
       [0, 0, 0, 3, 0],
       [0, 0, 0, 0, 4]])

# 对角线向上偏移一位
np.diag(a, 1)
array([[0, 0, 0, 0, 0, 0],
       [0, 0, 1, 0, 0, 0],
       [0, 0, 0, 2, 0, 0],
       [0, 0, 0, 0, 3, 0],
       [0, 0, 0, 0, 0, 4],
       [0, 0, 0, 0, 0, 0]])

# 对角线向下偏移一位
np.diag(a, -1)
array([[0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0],
       [0, 1, 0, 0, 0, 0],
       [0, 0, 2, 0, 0, 0],
       [0, 0, 0, 3, 0, 0],
       [0, 0, 0, 0, 4, 0]])

a1 = np.arange(9).reshape(3, 3)
a1
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

# 取上三角矩阵
np.triu(a1)
array([[0, 1, 2],
       [0, 4, 5],
       [0, 0, 8]])

# 上三角矩阵向左下偏移一位
np.triu(a1, -1)
array([[0, 1, 2],
       [3, 4, 5],
       [0, 7, 8]])

# 上三角矩阵向右上偏移一位
np.triu(a1, 1)
array([[0, 1, 2],
       [0, 0, 5],
       [0, 0, 0]])

# 下三角矩阵
np.tril(a1)
array([[0, 0, 0],
       [3, 4, 0],
       [6, 7, 8]])

3.NumPy中矩阵基本运算

  由于NumPy中我们使用二维数组来表述矩阵，因此二维数组也就具备了数组和矩阵的两重属性。其中数组属性决定的基本运算相对简单，基础运算（如加减乘除）就是对应位置元素进行逐元素计算，而矩阵属性决定的运算则稍显复杂，当然矩阵的相关线性代数运算将在下一小节讨论，在基础运算上，矩阵和数组核心的区别在于乘法运算。
  当然，从另一个角度考虑，其实对于向量和矩阵这种具备一定结构的对象，有很多种容易混淆的计算规则。对于常用的计算规则，我们通过将其划分成三类以帮助大家理解：

描述解释/函数
逐元素相乘向量、矩阵通用
每个对应位置元素相乘*
逐元素相乘后相加也被称为点积（内积），向量，矩阵通用
向量点积vdot、dot、inner
矩阵点积vdot
矩阵乘法代数学意义的矩阵相乘
矩阵乘法dot、matmul、@
  • * :逐元素相乘
a = np.arange(4)
a
array([0, 1, 2, 3])

a * a
array([0, 1, 4, 9])

A = a.reshape(2, 2)
A
array([[0, 1],
       [2, 3]])

A * A
array([[0, 1],
       [4, 9]])
  • 向量点积
      所谓点积（也被称为内积），指的是向量或矩阵对应位置元素相乘后相加。向量点积有三种实现方法，分别是dot、vdot和ineer。
np.dot(a, a)
14

a.dot(a)
14

(a * a).sum()
14

np.vdot(a, a)
14

np.inner(a, a)
14
  • 矩阵点积
      值得注意的是，矩阵内积只有vdot一种方式实现。
A
array([[0, 1],
       [2, 3]])

np.vdot(A, A)
14

(A * A).sum()
14

注意，高维数组的inner并不是内积，而是一种类似tensordot的沿着尾轴实现和积的计算过程，该方法并不通用，此处暂不做介绍。

  • 矩阵乘法
      NumPy中，我们可以使用诸多方法实现矩阵乘法，包括dot、@、matmul等。
a1 = np.arange(1, 7).reshape(2, 3)
a1
array([[1, 2, 3],
       [4, 5, 6]])

a2 = np.arange(1, 10).reshape(3, 3)
a2
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])


# 矩阵乘法
np.matmul(a1, a2)
array([[30, 36, 42],
       [66, 81, 96]])

此处也简单回顾矩阵乘法运算，上述相乘过程如下所示：
5

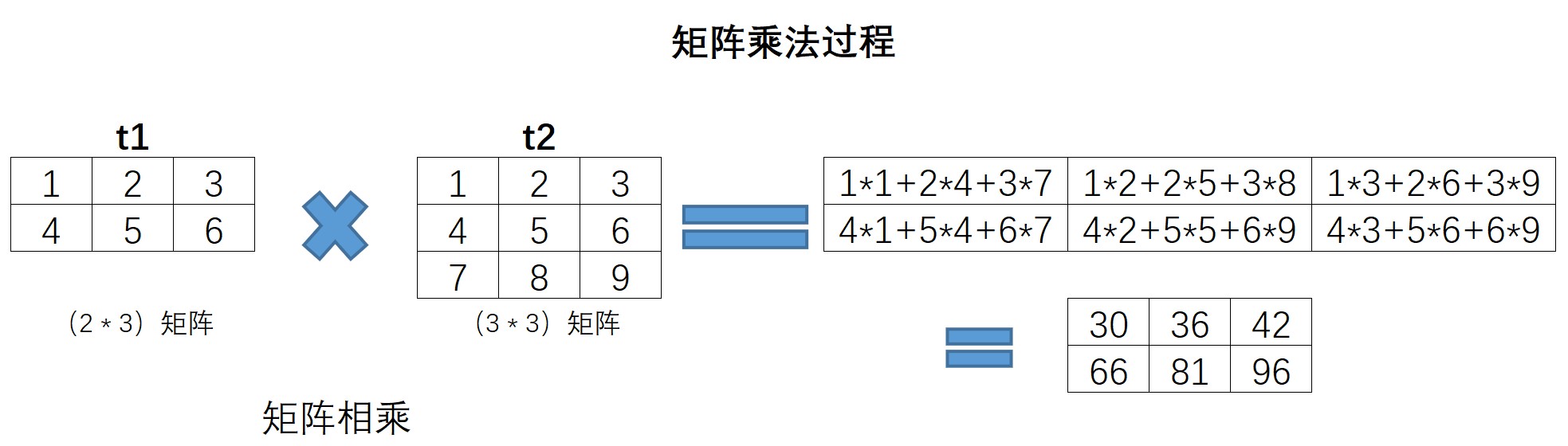
值得注意的是，矩阵相乘要求左乘矩阵列数和右乘矩阵行数相同，而内积计算过程则严格要求两个向量/矩阵形状完全一致。

4.NumPy中矩阵代数运算

  如果说矩阵的基本运算是矩阵基本性质，那么矩阵的线性代数运算，则是我们利用矩阵数据类型在求解实际问题过程中经常涉及到的线性代数方法，具体相关函数如下：

矩阵的线性代数运算

函数描述
np.trace(A)矩阵的迹
np.linalg.matrix_rank(A)矩阵的秩
np.linalg…det(A)计算矩阵A的行列式
np.linalg.inv(A)矩阵求逆

同时，由于线性代数所涉及的数学基础知识较多，从实际应用的角度出发，我们将有所侧重的介绍实际应用过程中需要掌握的相关内容，并通过本节末尾的实际案例，来加深线性代数相关内容的理解。

NumPy中的linalg是linear algebra（线性代数）的简写，也是NumPy中保存线性代数相关计算函数的模块。

  • 矩阵的迹（trace）

  矩阵的迹的运算相对简单，就是矩阵对角线元素之和，在NumPy中，可以使用trace函数进行计算。

A = np.array([[1, 2], [4, 5]])
A
array([[1, 2],
       [4, 5]])

np.trace(A)
6

当然，对于矩阵的迹来说，计算过程不需要是方正

B = np.arange(1, 7).reshape(2, 3)
B
array([[1, 2, 3],
       [4, 5, 6]])

np.trace(B)
6
  • 矩阵的秩(rank)
      矩阵的秩（rank），是指矩阵中行或列的极大线性无关数，且矩阵中行、列极大无关数总是相同的，任何矩阵的秩都是唯一值，满秩指的是方阵（行数和列数相同的矩阵）中行数、列数和秩相同，满秩矩阵有线性唯一解等重要特性，而其他矩阵也能通过求解秩来降维，同时，秩也是奇异值分解等运算中涉及到的重要概念。

所谓线性相关，其实也就是线性表示，如果 y = w x + b y=wx+b y=wx+b，我们则称y可以由x线性表示，二者线性相关，反之则线性无关。类似，如果 y = w 1 x 1 w 2 x 2 + b y=w_1x_1w_2x_2+b y=w1​x1​w2​x2​+b，则我们称y可以由 x 1 、 x 2 x_1、x_2 x1​、x2​线性表示，y与 x 1 、 x 2 x_1、x_2 x1​、x2​线性相关。

  • matrix_rank计算矩阵的秩
A = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 2]])
A
array([[1, 3, 4],
       [2, 1, 3],
       [1, 1, 2]])

np.linalg.matrix_rank(A)
2

对于矩阵A来说，第三列明显可以由第一列和第二列相加得出，因此极大线性无关组只有两列。

B = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 10]])
B
array([[ 1,  3,  4],
       [ 2,  1,  3],
       [ 1,  1, 10]])

np.linalg.matrix_rank(B)
3
  • 矩阵的行列式(det)
      所谓行列式，我们可以简单将其理解为矩阵的一个基本性质或者属性，通过行列式的计算，我们能够知道矩阵是否可逆，从而可以进一步求解矩阵所对应的线性方程。当然，更加专业的解释，行列式的作为一个基本数学工具，实际上就是矩阵进行线性变换的伸缩因子。

对于任何一个n维方正，行列式计算过程如下：
7

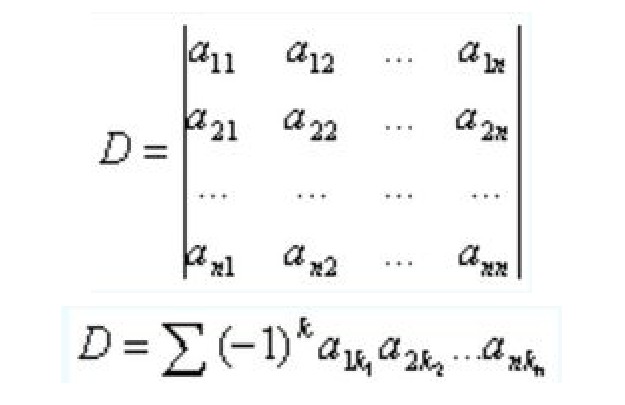
更为简单的情况，如果对于一个2*2的矩阵，行列式的计算就是主对角线元素之积减去另外两个元素之积

A = np.array([[1, 2], [4, 5]])
A
array([[1, 2],
       [4, 5]])

np.linalg.det(A)
-2.9999999999999996

A的秩计算过程如下：
6

对于行列式的计算，要求矩阵必须是方阵，也就是行列数必须一致。

B = np.arange(1, 7).reshape(2, 3)
B
array([[1, 2, 3],
       [4, 5, 6]])

np.linalg.det(B)

A = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 2]])
A
array([[1, 3, 4],
       [2, 1, 3],
       [1, 1, 2]])
       
np.linalg.det(A)
0.0
  • 矩阵的逆
      对于满秩的方正来说，可以求其逆矩阵。从基本定义上来看，如果矩阵B和矩阵A相乘能够得到单位矩阵，即：
    B ⋅ A = E B \cdot A = E B⋅A=E

则称B为A的逆矩阵，也可将B写作 A − 1 A^{-1} A−1。当然，逆矩阵的性质是相互的，我们也可称A为B的逆矩阵，或者A和B互为逆矩阵。

A = np.array([[1, 1], [3, 1]])
A
array([[1, 1],
       [3, 1]])

然后使用inverse函数进行逆矩阵求解

np.linalg.inv(A)
array([[-0.5,  0.5],
       [ 1.5, -0.5]])

简单试探逆矩阵的基本特性

A.dot(np.linalg.inv(A))
array([[1.00000000e+00, 1.11022302e-16],
       [2.22044605e-16, 1.00000000e+00]])

当然，对于逆矩阵，还有很多其他理解角度。例如，从方程组求解角度来看，逆矩阵的存在就代表着方程组存在唯一解，并且逆矩阵本身也是方程组求解的关键；从矩阵分解角度来看，逆矩阵是一种最为基础的矩阵分解的形式。关于这些相关内容，我们都将在后续课程中逐渐介绍。

另外，在本栏目内容中，我们还将介绍solve（方程组求解）、lstsq（最小二乘法）相关函数的使用。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1522475.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

FFmpeg转码参数说明及视频转码示例

FFmpeg转码参数说明及视频转码示例

-b : 设置音频或者视频的转码码率 -b:v 只设置视频码率 -b:a 只设置音频码率 -ab: 只设置音频码率, 默认码率大小为: 128k bit/s -g: 设置视频GOP大小,表示I帧之间的间隔,默认为12 -ar: 设置音频采样率,默认0 -ac: 设置音频通道数量 默认0 -bf: 设置连…
阅读更多...
服务器机器学习环境搭建（包括AanConda的安装和Pytorch的安装）

服务器机器学习环境搭建（包括AanConda的安装和Pytorch的安装）

服务器机器学习环境搭建 1 服务器与用户 在学校中，我们在学校中是以用户的身份进行访问学校的服务器的。整体框架大致如下： 我们与root用户共享服务器的一些资源，比如显卡驱动，Cuda以及一些其他的公共软件。 一般情况下&#…
阅读更多...
Vue2在一个页面内动态切换菜单显示对应的路由组件

Vue2在一个页面内动态切换菜单显示对应的路由组件

项目的需求是在一个页面内动态获取导航菜单，导航菜单切换的时候显示对应的路由页面，类似于tab切换的形式，切换的导航菜单和页面左侧导航菜单是同一个路由组件，只是放到了一个页面上，显示的个数不同，所有是动…
阅读更多...
Docker----Dockerfile构建微服务镜像

Docker----Dockerfile构建微服务镜像

目录 一、关键步骤 二、具体步骤 1、准备后端jar包(这里以java后端演示) 2、编写Dockerfile 3、构建镜像 4、运行镜像容器 5、测试是否成功 一、关键步骤 1、准备后端jar包(这里以java后端演示) 2、编写Dockerfile 3、构建镜像 4、运行镜像容器 5、测试是否成功 二…
阅读更多...
C#，图论与图算法，图（Graph）的数据结构设计与源代码

C#，图论与图算法，图（Graph）的数据结构设计与源代码

因为后面即将发布的大量有关“图”的算法与源代码都需要用到下面的这些基础数据，为避免大家去下载，特意先发布于此。 一、图（Graph）的基础知识 图（Graph）是一组对象的图示，其中一些对象对通过链…
阅读更多...
STM32(TIM定时器中断)

STM32(TIM定时器中断)

理论知识 定时器定时中断 接线图 定时器工作配置步骤 定时中断和内外时钟源选择 定时器中需要使用的函数 程序实现效果： void TIM_DeInit(TIM_TypeDef* TIMx); **// 恢复定时器的缺省配置**void TIM_TimeBaseInit(TIM_TypeDef* TIMx, TIM_TimeBaseInitTypeDef*TIM…
阅读更多...
jupyter中pip安装包会安装到别的环境。

jupyter中pip安装包会安装到别的环境。

文章目录 1. 查看jupyter当前环境和默认环境的路径和python版本2.安装包到正确的环境 如果你在 Jupyter Notebook 中使用 pip 安装包，它默认会将包安装到 Jupyter Notebook 所在的Python 环境。这可能会导致安装的包与你期望的环境不匹配。 1. 查看jupyter当前环境和…
阅读更多...
RK3568平台开发系列讲解（基础篇）内核是如何发送事件到用户空间

RK3568平台开发系列讲解（基础篇）内核是如何发送事件到用户空间

🚀返回专栏总目录 文章目录 一、相关接口函数二、udevadm 命令三、实验沉淀、分享、成长，让自己和他人都能有所收获！😄 一、相关接口函数 kobject_uevent 是 Linux 内核中的一个函数， 用于生成和发送 uevent 事件。 它是 udev 和其他设备管理工具与内核通信的一种方式。…
阅读更多...
mybatis源码阅读系列（二）

mybatis源码阅读系列（二）

前言 上一篇文章mybatis源码阅读系列（一）介绍了mybatis和原生jdbc的区别，并通过代码展示了两者的运行过程和结果，下面让我们继续详细了解下mybatis的执行过程； package com.wyl.mybatis.service;import com.wyl.mybat…
阅读更多...
给定参数c和长度为n的递增数组a(ai ＜= c), 对于0＜=x＜=y＜=c, 求（x，y）的对数，满足x+y不是数组a中的元素且y-x不是a中元素

给定参数c和长度为n的递增数组a(ai ＜= c), 对于0＜=x＜=y＜=c, 求（x，y）的对数，满足x+y不是数组a中的元素且y-x不是a中元素

题目 思路&#xff1a; #include <bits/stdc.h> using namespace std; #define int long long #define pb push_back #define fi first #define se second #define lson p << 1 #define rson p << 1 | 1 const int maxn 1e6 5, inf 1e18, maxm 4e4 5, …
阅读更多...
微信小程序关闭首页广告

微信小程序关闭首页广告

由于之前微信小程序默认开启了首页广告位。导致很多老人误入广告页的内容&#xff0c;所以想着怎么屏蔽广告。好家伙&#xff0c;搜索一圈&#xff0c;要么是用户版本的屏蔽广告&#xff0c;或者是以下一个模棱两可的答案&#xff0c;要开发者设置一下什么参数的&#xff0c;如…
阅读更多...
Opencascade基础教程（11）：设置显示模式

Opencascade基础教程（11）：设置显示模式

1、设置显示模式 1.1 增加按钮添加消息响应函数 //线框 void COCCDemoDoc::OnButtonWireframemode() {//关闭边界框const Handle(Prs3d_Drawer)& aDrawer m_AISContext->DefaultDrawer();aDrawer->SetFaceBoundaryDraw(false);//线框m_AISContext->SetDisplayMo…
阅读更多...
【SQL】1193. 每月交易 I 【年月日（日期）拼接相关函数】

【SQL】1193. 每月交易 I 【年月日（日期）拼接相关函数】

前述 知识点学习&#xff1a; SQL 日期函数 day() 、month()、year() 各种使用方法mysql 两个字符年月拼接 题目描述 leetcode题目&#xff1a;1193. 每月交易 I 思路 先按照年月排&#xff0c;再按照country排列 日期拼接相关的函数 year(): 截取年份&#xff1b;month…
阅读更多...
springboot蛋糕订购小程序的设计与实现

springboot蛋糕订购小程序的设计与实现

摘 要 相比于以前的传统手工管理方式&#xff0c;智能化的管理方式可以大幅降低商家的运营人员成本&#xff0c;实现了蛋糕订购的标准化、制度化、程序化的管理&#xff0c;有效地防止了蛋糕订购的随意管理&#xff0c;提高了信息的处理速度和精确度&#xff0c;能够及时、准确…
阅读更多...
如何重置iPhone的网络设置？这里提供详细步骤

如何重置iPhone的网络设置？这里提供详细步骤

前言 本文介绍如何重置iPhone上的网络设置。该信息适用于iPhone 12到iPhone 6以及iOS 14到iOS 8。 如何在iPhone上重置网络设置 采取以下步骤重置iPhone上的网络设置&#xff1a; 1、在iPhone上&#xff0c;打开设置应用程序。 2、单击通用。 3、滚动到屏幕底部&#xff…
阅读更多...
如何保存缓存和MySQL的双写一致呢？

如何保存缓存和MySQL的双写一致呢？

如何保存缓存和MySQL的双写一致呢&#xff1f; 所谓的双写一致指的是&#xff0c;在同时使用缓存(如Redis)和数据库(如MySQL)的场景下,确保数据在缓存和数据库中的更新操作保持一致。当对数据进行修改的时候&#xff0c;无论是先修改缓存还是先修改数据库&#xff0c;最终都要保…
阅读更多...
深度学习-解读GoogleNet深度学习网络

深度学习-解读GoogleNet深度学习网络

深度学习-解读GoogleNet深度学习网络 深度学习中&#xff0c;经典网络引领一波又一波的技术革命&#xff0c;从LetNet到当前最火的GPT所用的Transformer&#xff0c;它们把AI技术不断推向高潮。2012年AlexNet大放异彩&#xff0c;它把深度学习技术引领第一个高峰&#xff0c;打…
阅读更多...
双向SSM: Vision Mamba Encoder

双向SSM: Vision Mamba Encoder

文章目录 Vision Mamba Encoder初始化输入映射序列变换参数映射BC参数映射delta参数映射 SSM参数初始化A , D矩阵初始化delta参数初始化 双向SSM初始化参数初始化 前向输入映射fast_pathuse_fast_pathno use_fast_path 双向SSMv1前向后向 v2前向后向 Vision Mamba Encoder Vis…
阅读更多...
（四）Android布局类型（线性布局LinearLayout）

（四）Android布局类型（线性布局LinearLayout）

线性布局&#xff08;LinearLayout&#xff09;&#xff1a;按照一定的方向排列组件&#xff0c;方向主要分为水平方向和垂直方向。方向的设置通过属性android:orientation设置 android:orientation 其取值有两种 水平方向&#xff1a;android:orientation"horizontal&…
阅读更多...
蓝桥杯单片机快速开发笔记——独立键盘

蓝桥杯单片机快速开发笔记——独立键盘

一、原理分析 二、思维导图 三、示例框架 #include "reg52.h" sbit S7 P3^0; sbit S6 P3^1; sbit S5 P3^2; sbit S4 P3^3; void ScanKeys(){if(S7 0){Delay(500);if(S7 0){while(S7 0);}}if(S6 0){Delay(500);if(S6 0){while(S6 0)…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023