刷题日记——非素数个数（厦大机试）

news2024/11/17 12:55:19

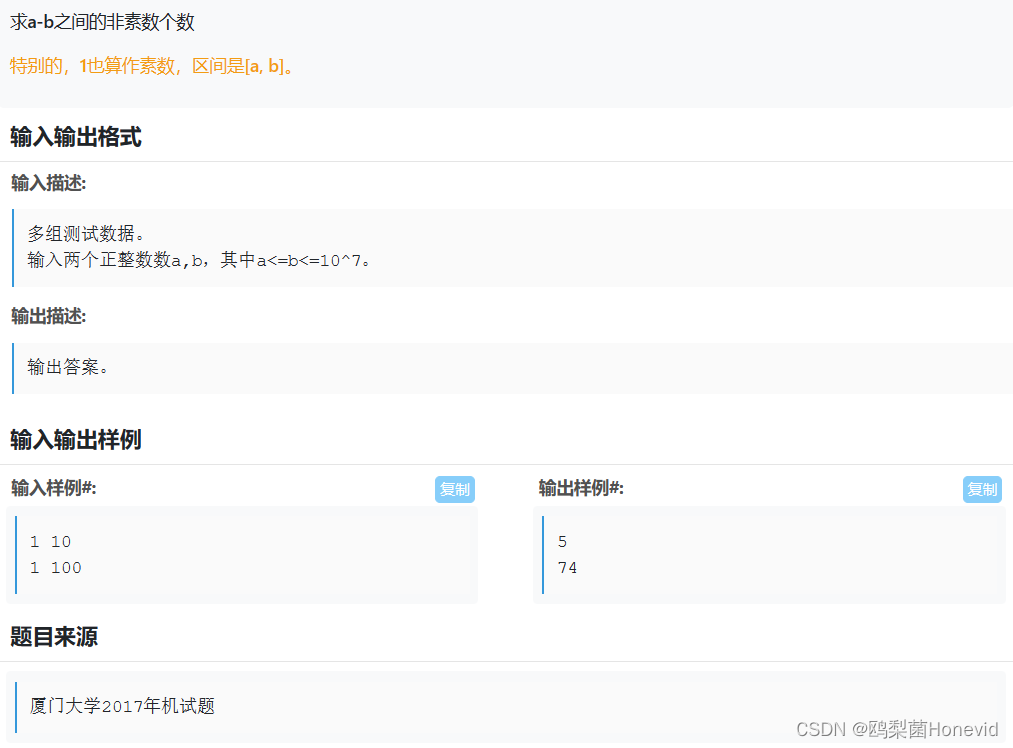
题目

在这里插入图片描述

分析

使用欧拉筛法计算从1到b的素数个数，方法如下：
找到一个素数后，就将它的倍数标记为合数，也就是把它的倍数“筛掉”；如果一个数没有被比它小的素数“筛掉”，那它就是素数。
计算出从1到b的素数过后，会留下一个装满从1到b内所有素数的数组，该数组大小即为从1到b的素数个数 $count_b$ ，我们遍历数组，对小于a的素数个数进行计数，计数值即为1到a的素数个数 $count_a$
那么从a到b的素数个数为: $count_b-count_a$
从a到b的非素数个数为: $b-a+1+count_b-count_a$ （注意a≠1时成立）
注意，题目要求1也算作素数，那么在a=1时，从a到b的非素数个数为: $b-a+count_b-count_a$

代码

#include <cstdio>
#include <map>
#include <string>
#include <string.h>
#include <cmath>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <limits.h>
using namespace std;
bool is_su[10000001];
int su[10000001];

int num_of_su(int n){
  int counts = 0;
  for(int i=2;i<=n;i++){
    if(is_su[i]){
      su[++counts] = i;
    }
    for(int j=1;j<=counts&&i*su[j]<=n;j++){
      is_su[i*su[j]] = false;
      if(i%su[j]==0){
        break;
      }
    }
  }
  return counts;
}

int main(){
  int a,b;
  while(scanf("%d%d",&a,&b)!=EOF){
    int counts_a = 0;
    int counts_b = 0;
    memset(is_su, true, b+1);
    is_su[1]=false;
    counts_b = num_of_su(b);
    for(int i=1;su[i]<a;i++){
      counts_a++;
    }
    int result = b-a-counts_b+counts_a+1;
    if(a==1){
      result--;
    }
    printf("%d\n",result);
  }

	return 0;
}