目录

一，3074. 重新分装苹果

二，3075. 幸福值最大化的选择方案

三，3076. 数组中的最短非公共子字符串

四，3077. K 个不相交子数组的最大能量值

---

一，3074. 重新分装苹果

本题是一道阅读理解题，就是将数组apple中的所有苹果全部放入capacity中，问最少需要多少个箱子。先算出总的苹果树，再将箱子从小到大排序，然后将苹果放入箱子（从大到小放），代码如下：

class Solution {
    public int minimumBoxes(int[] apple, int[] capacity) {
        int sum = 0;
        for(int x : apple)
            sum += x;
        Arrays.sort(capacity);
        int n = capacity.length;
        for(int i=n-1; i>=0; i--){
            sum -= capacity[i];
            if(sum <= 0)
                return n-i;
        }
        return -1;
    }
}

二，3075. 幸福值最大化的选择方案

本题也是阅读理解题，本质就是贪心，从大到小选择，每选择一个孩子，那么剩下的孩子的幸福值全部减一且幸福值不会小于零(即幸福值>=0)。代码如下：

class Solution {
    public long maximumHappinessSum(int[] happiness, int k) {
        Arrays.sort(happiness);
        int j = 0;
        int n = happiness.length;
        long ans = 0;
        for(int i=n-1; i>=0&&j<k; i--){
            if(happiness[i] > j){
                ans += happiness[i]-j;
                j++;
            }else
                return ans;
        }
        return ans;
    }
}

三，3076. 数组中的最短非公共子字符串

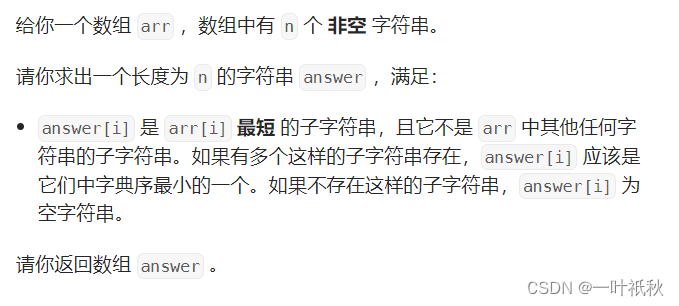
本题数据范围较小，可以直接暴力求解，代码如下：

class Solution {
    public String[] shortestSubstrings(String[] arr) {
        int n = arr.length;
        String[] ans = new String[n];
        for (int i = 0; i < n; i++) {
            int m = arr[i].length();
            String res = "";
            for (int size = 1; size <= m && res.isEmpty(); size++) {
                for (int j = size; j <= m; j++) {
                    String t = arr[i].substring(j - size, j);
                    if ((res.isEmpty() || t.compareTo(res) < 0) && check(arr, i, t)) {
                        res = t;
                    }
                }
            }
            ans[i] = res;
        }
        return ans;
    }

    private boolean check(String[] arr, int i, String sub) {
        for (int j = 0; j < arr.length; j++) {
            if (j != i && arr[j].contains(sub)) {
                return false;
            }
        }
        return true;
    }
}

四，3077. K 个不相交子数组的最大能量值

划分dp

定义 f [ i ][ j ] 表示将前 j 个数分成 i 段所得到的最大值

根据题目要求，f [ i ] [ j ] 的转移来源有两个：

1. 不选择当前数，那么f[ i ][ j ]可以等价于将前 j - 1 个数分成 i 段所得到的最大值， 即 f [ i ][ j-1 ]
2. 选择当前数，设选择的子数组的范围是[L，j）该子数组的和为 pre[ j ] - pre[ L ]，那么当前的转移方程是 f [i - 1][ L ] + (k-i+1) * (-1)^(i+1) * (pre[ j ]- pre[ L ] )

可以得到如下的递推方程：

f [ i ][ j ] = Math.max( f [ i ][ j - 1]，f [i - 1][ L ] + (k-i+1) * (-1)^(i+1) * (pre[ j ]- pre[ L ] ) )

可以看出来，如果要计算上述 f [ i ][ j ]，需要遍历三个未知数 i ，j，L，这样的话就会超时，所以还要优化。可以将上述的方程因式分解：

设 w = (-1)^(i+1)

f [ i ][ j ] = Math.max( f [ i ][ j - 1]，f [i - 1][ L ] + w * (pre[ j ] - pre[ L ] ) )

              = Math.max( f [ i ][ j - 1]，f [i - 1][ L ] - w * pre[ L ] + w * pre[ j ] )

可以看出只有 mx =  f [i - 1][ L ] - w * pre[ L ] 与 L 有关系，能否将 L 这层循环省略：

当 j = i 时，计算 L = { i - 1 } 

当 j = i+1时，计算 L = { i - 1，i }

当 j = i+2时，计算 L = { i - 1，i，i + 1 }

.....

可以看出 L 除了等于 j-1时没有重复计算，其他情况一直在重复计算，通过这一特点，就可以将L这层循环给省略掉了。

注：i <= j，因为要将 j 个数分成 i 段，那么至少也要有 i 个数

代码如下：

class Solution {
    public long maximumStrength(int[] nums, int k) {
        //f[i][j]:前j个数分成i段
        //f[i][j] = Max(f[i][j-1], f[i][L]+(k-i+1)*(-1)^k*(pre[j]-pre[l]))
        int n = nums.length;
        long[][] f = new long[k+1][n+1];
        long[] pre = new long[n+1];
        for(int i=0; i<n; i++)
            pre[i+1] = pre[i] + nums[i];
        for(int i=1; i<k+1; i++){
            f[i][i-1] = Long.MIN_VALUE/2;
            long mx = Long.MIN_VALUE/2;
            int w = (k-i+1)*(i%2==1?1:-1);
            for(int j=i; j<=n-k+i; j++){
                mx = Math.max(mx, f[i-1][j-1]-w*pre[j-1]);
                f[i][j] = Math.max(f[i][j-1], mx + w*pre[j]);
            }
        }
        return f[k][n];
    }
}