树的概念

1.树是一种非线性的数据结构。它是由n个有限节点的集合。

2.树分为根节点和子树。根节点没有前驱节点。

3.树的子树是由一个个子树组成，它们可以看作一个个集合。每个集合下面又有集合。

因此，树是递归定义的。

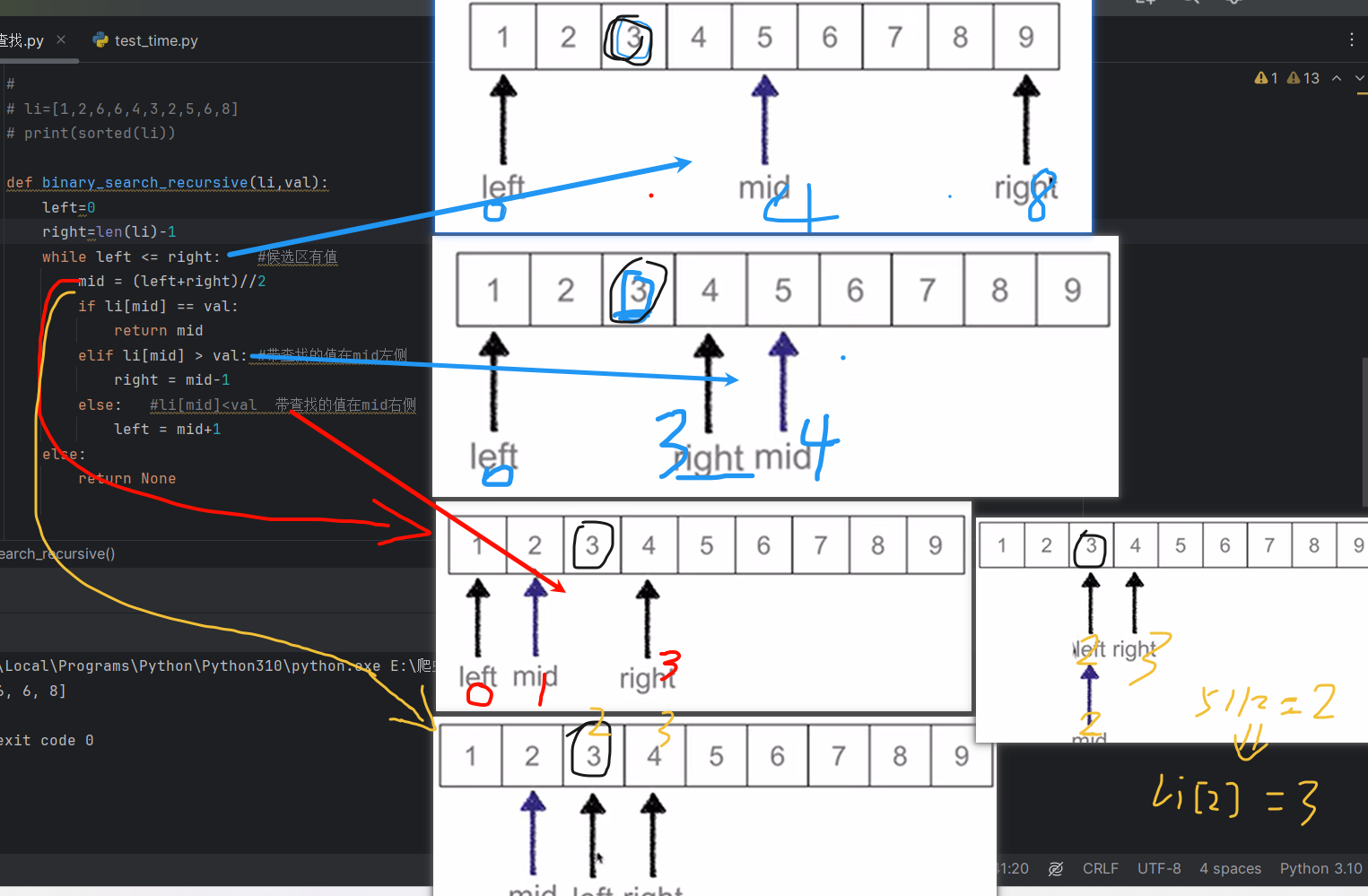
树形结构中，子树之间不能有交集，除了根节点外，每个节点只有一个父节点。一颗N节点的树，有N-1条边。

如上图所示，F节点是所有节点的根节点，也是祖先节点。D是F的孩子节点，是左孩子。ABC是F的子孙节点。

树的表示，一般采用最常用的孩子兄弟表示法。

树节点的第一个指针指向左边第一个孩子，第二个指针指向它的兄弟节点。

typedef int DataType;
struct Node
{
   struct Node * firstchild;
   struct Node * pnextbrother;
   DataType data;
};

树在实际中的应用：

表示文件系统的目录。

windows文件下也有众多文件，当访问时，就会出现在用户面前，这些访问就通过树的访问方式进行访问的。

二叉树概念及结构

概念

在之前树的概念的基础上，限制了度。二叉树的度不超过2。也就是说，二叉树的所有节点的孩子，最多只能有两个。

二叉树的子树有左右之分，因此是有序的树。

下图是满二叉树。

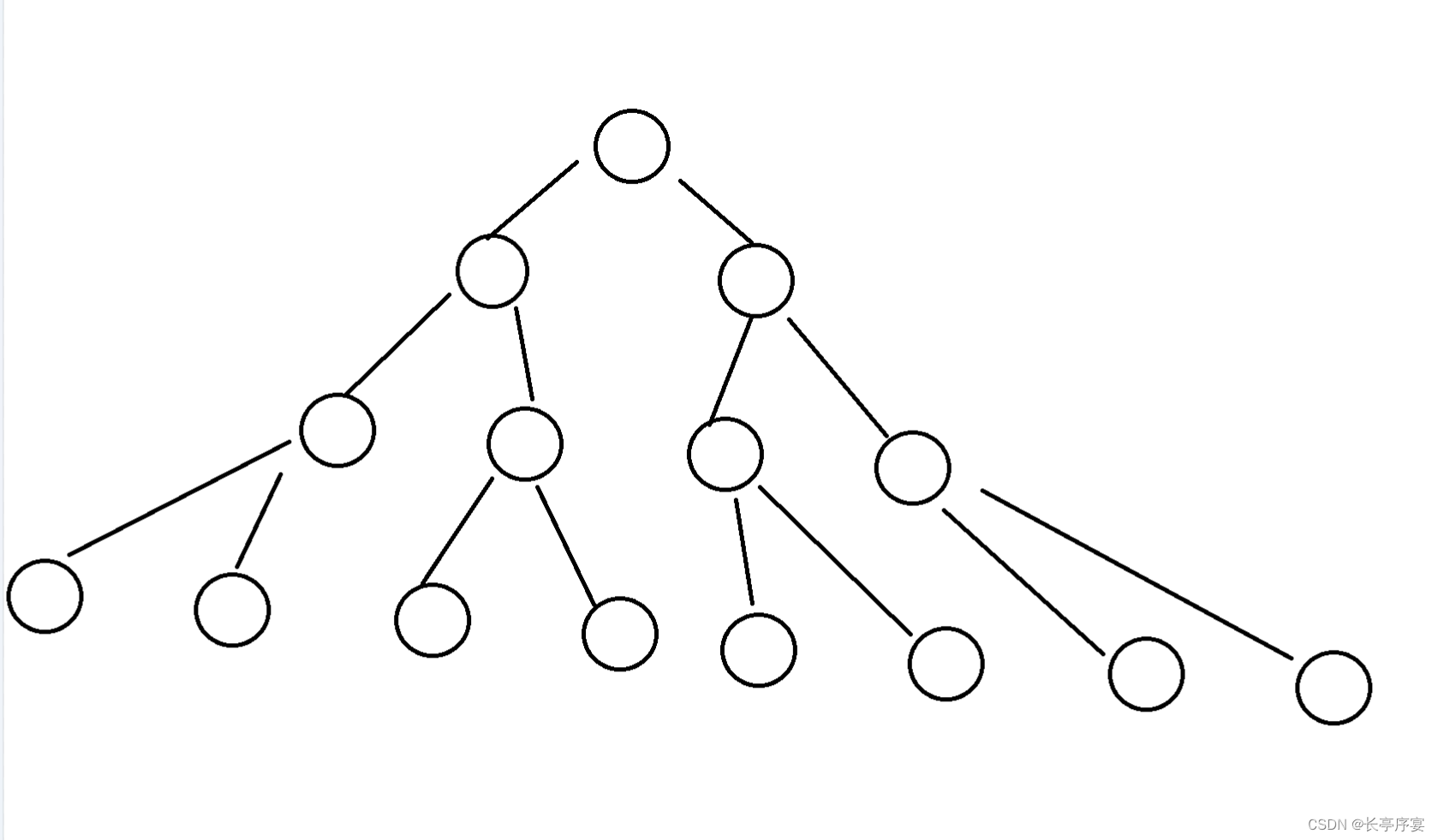
下图为完全二叉树

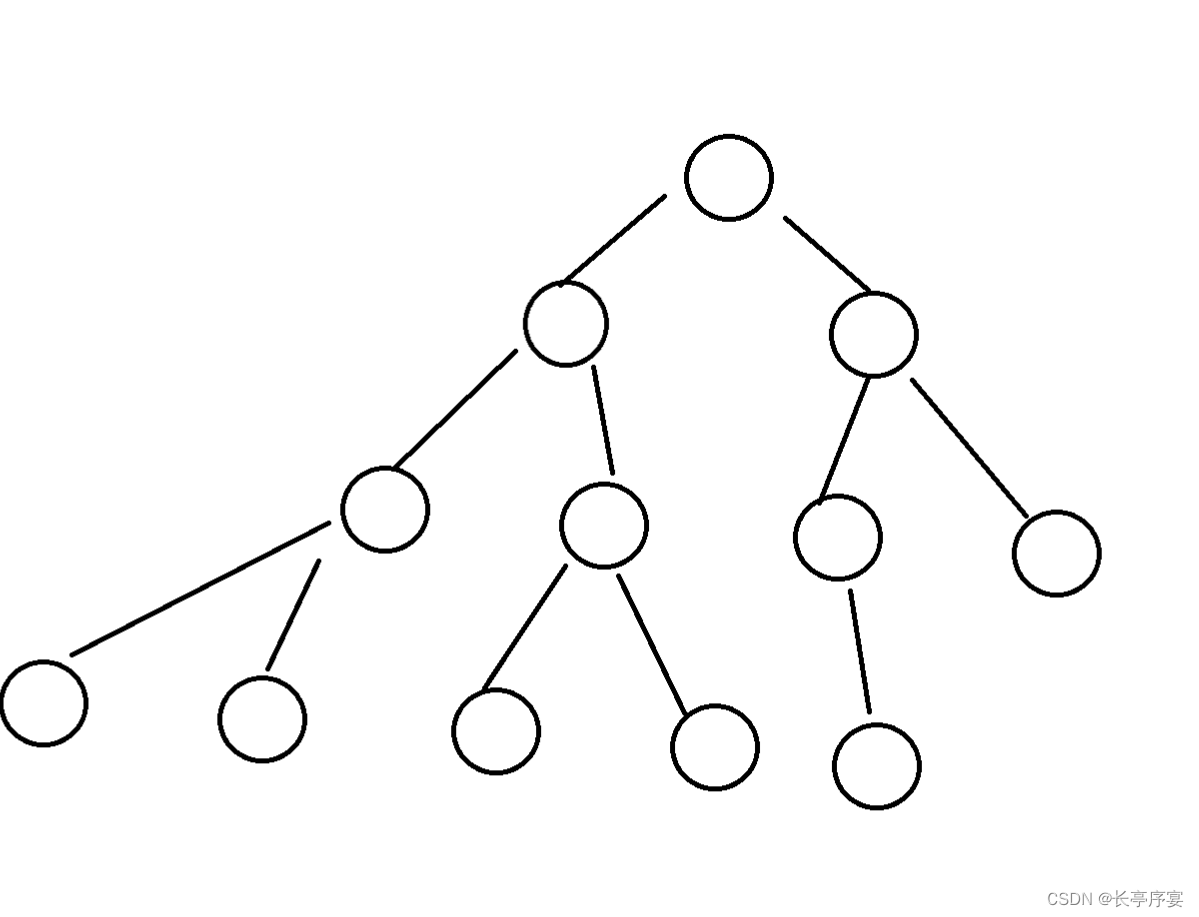
满二叉树的特征：

每一层的结点数都达到最大值。

如果它的层数为h，那么总结点数为2^h-1.

完全二叉树的特征：

完全二叉树是中间没有漏节点的有序的二叉树，它是由满二叉树引申来的

二叉树的性质：

1.如果根节点是第1层，那么一颗非空二叉树的第i层上最多有2^(i-1)个节点。

2.如果根节点是第1层，那么深度为h为的二叉树最大节点数是2^h-1。

3.对任何一棵二叉树，如果度为0的叶子节点数是N0，度为2的节点数为N2，则有N0=N2+1。

4.若规定根节点是第一层，具有n个节点的满二叉树的深度为h=log(N+1).

5.对于具有n个节点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号。则对于序号为i的节点有：

       1.若i > 0,i位置节点的双亲序号： (i-1) / 2;

       2.若 2i+1 < n , 左孩子序号： 2i+1， 2i+1>=n 则无右孩子。

       3.若 2i+2 < n,右孩子序号：2i+2,    2i+2  >=n  则无右孩子。