本次的题与动态规划7 的题有相似与共通之处,建议先去看 动态规划7:动态规划7
摆动序列

什么是摆动序列? 就像这种:
一个数,一个下降,上升,来回上升下降都可以叫摆动序列。

思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子序列中,最长摆动序列的长度。
对于本题,如果只定一个状态数组是不够的,因为我们只有区分了 i 位置是在增长还是在降低,才能判断 i + 1 位置是否能续上前面的波浪。所以,我们需要定义两个状态数组,分别表示以 i 结尾的在增长和降低的最长摆动序列长度。
f[i] 表示:以i 位置为结尾的所有子序列中,最后呈现 “ 上升” 状态下的最长摆动序列长度。
g[i] 表示:以i 位置为结尾的所有子序列中,最后呈现 “ 下降” 状态下的最长摆动序列长度。
-
状态转移方程
对于 f[i] 来讲,当长度为1,意味着只有这一个数的时候,长度为1,因为他本身就可以构成摆动序列
当长度大于1,并且以nums[i] > nums[j] 的前提下,(j的范围为0 ~ i-1 , 因为子序列是可以删除一些原始数组元素的)
f[i] 就等于 max(g[i] + 1, f[i]), 为什么有max操作,因为每次都要最长摆动序列的长度。
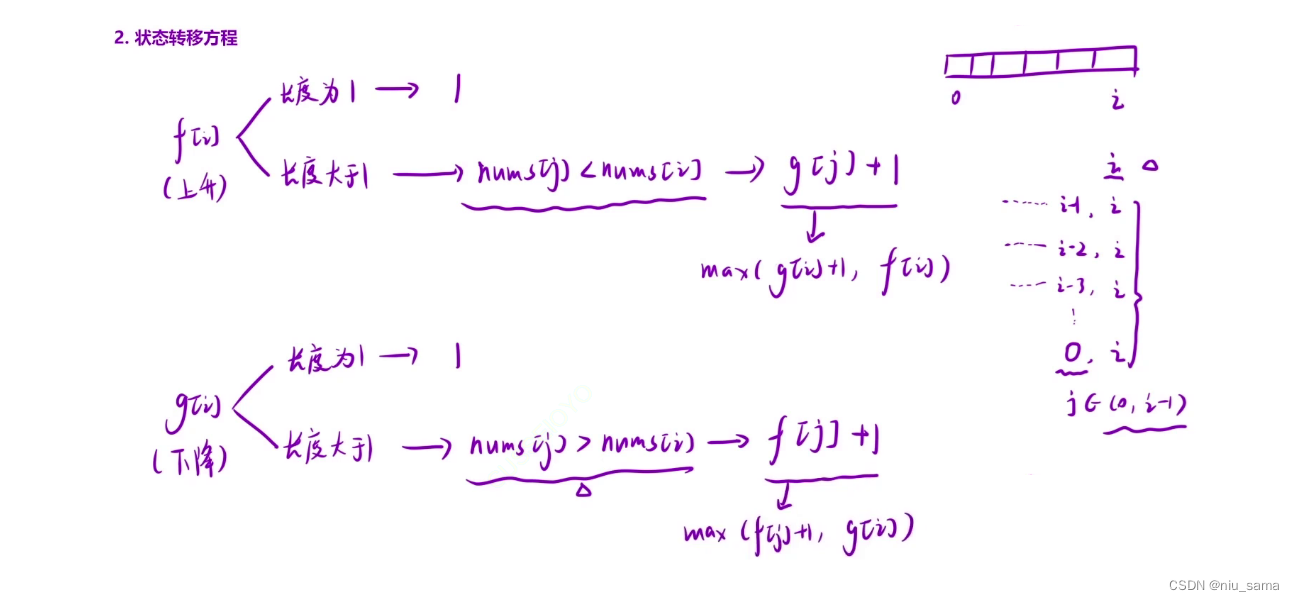
-
初始化
f表和g表全部都初始化为1,这样的好处是不用考虑两者长度为1的情况了。 -
填表顺序
从左向右填写,两个表一起填。
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
vector<int> up(n,1);
auto down = up;
int ret = 1;
for(int i = 1; i<n; i++)
{
for(int j = 0; j<i; j++)
{
if(nums[i] > nums[j])
up[i] = max(down[j]+1,up[i]);
else if(nums[i] < nums[j])
down[i] = max(up[j]+1,down[i]);
ret = max(ret,max(up[i],down[i]));
}
}
return ret;
}
};
最长递增子序列的个数

小 demo:一次遍历找到数组中最大值出现的次数

思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子序列中,最长递增子序列的个数。
对于本题,如果只定一个状态数组是不够的,因为我们既要知道最长递归子序列长度,还要知道最长长度有几个。所以,我们需要定义两个状态数组,分别表示以 i 结尾的最长递增子序列的长度和个数。
len[i]表示:以i 位置为结尾的所有子数组中,最长递增子序列的长度。
count[i]表示:以i 位置为结尾的所有子数组中,最长递增子序列的个数。
- 状态转移方程
对于len的分析,和上一道题一样,只不过是上一道题的增区间。

对于count的分析,我们要和len放到一起:
对于单独的一个数,len和count都为1,
如果满足nums[i] > nums[j] ,并且 当len[j] +1 等于 len[i]的情况,就是j位置的最大长度 加上一个新的 i 位置 正好是leni ,这时候count[i] 不能+1,假如前面有5个最长长度的,新加上 i 位置的,那不还是5个最长长度,所以为
count[i] += count[j].
如果为len[j] + 1 < len[i] 无视
如果为len[j] + 1 > len[i] ,更新最大值,让len[i] = len[j]+1 , count[i] = count[j];
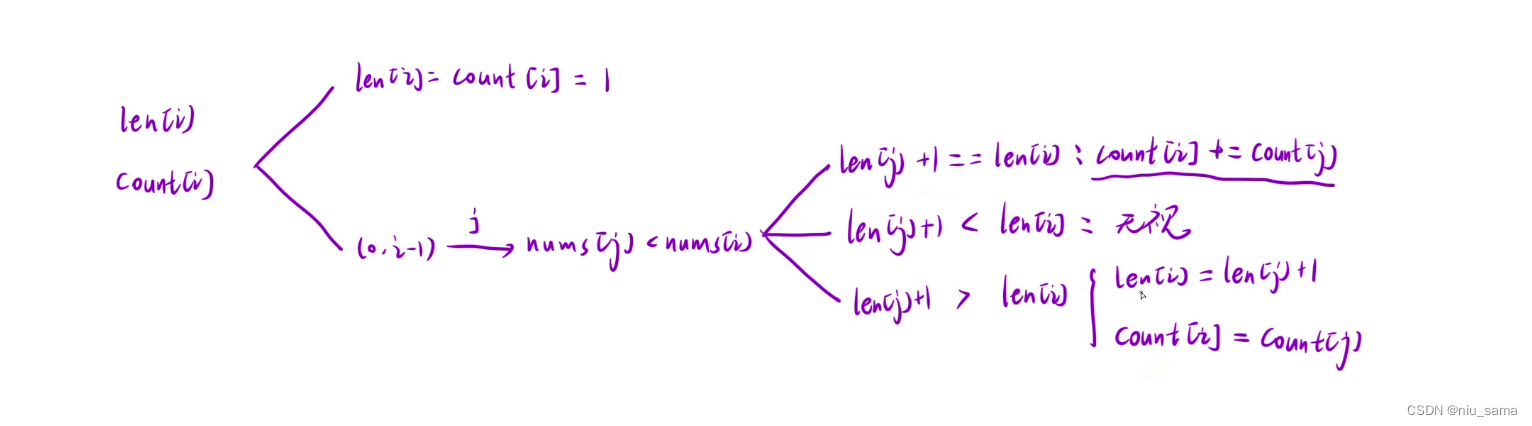
-
初始化
两个表都初始化为1; -
填表顺序
从左往右,两个表一起填写
class Solution {
public:
int findNumberOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> len(n,1);
auto count = len;
int relen = 1;
int recount = 1;
for(int i = 1; i<n; i++)
{
for(int j = 0; j<i; j++)
{
if(nums[i] > nums[j])
{
if(len[j]+1 == len[i])
count[i]+=count[j];
if(len[j] + 1 > len[i])
{
len[i] = len[j]+1;
count[i] = count[j];
}
}
}
if(relen == len[i]) recount+=count[i];
else if(relen < len[i]) relen = len[i], recount = count[i];
}
return recount;
}
};
最长数对链

当我们在分析的过程中,我们会发现当后面的数对不按顺序的时候,可以填后面的值有很多,比如示例二:后面的【7,8】和【4,5】没按顺序,两个都可以填到后面,所以我们要进行预处理:按照第一个元素排序即可。
思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有数对链中,最长的数对链个数。
-
状态转移方程
跟之前的题分析过程基本一样,就是变成数对了。
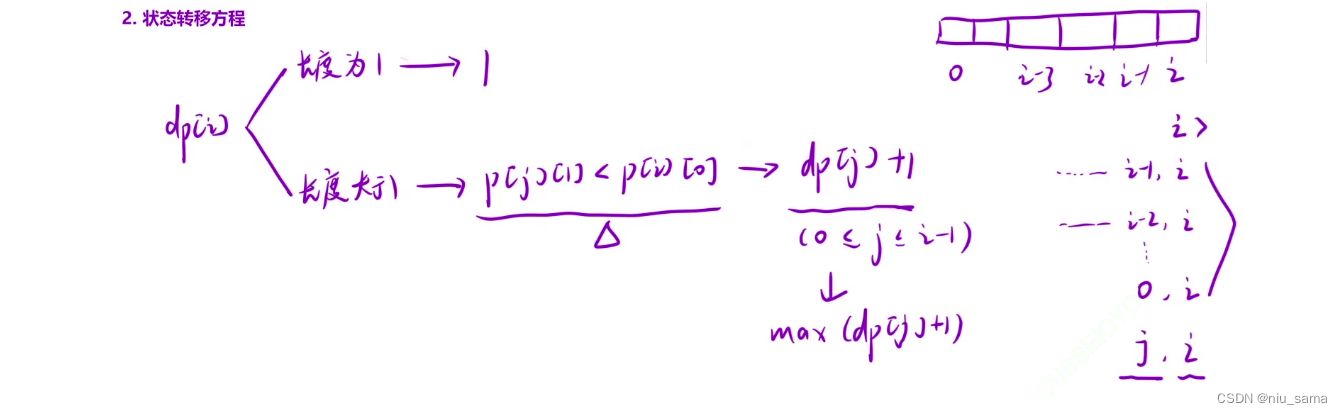
-
初始化
全部初始化为1. -
填表顺序
从左往右
class Solution {
public:
int findLongestChain(vector<vector<int>>& pairs) {
sort(pairs.begin(),pairs.end());
int n = pairs.size();
vector<int> dp(n,1);
int ret= 1; //可以防止pairs里面只有一对数对的情况
for(int i = 1; i<n; i++)
{
for(int j = 0; j<i; j++)
{
if(pairs[i][0] > pairs[j][1])
dp[i] = max(dp[j]+1,dp[i]);
}
ret = max(ret,dp[i]);
}
return ret;
}
};