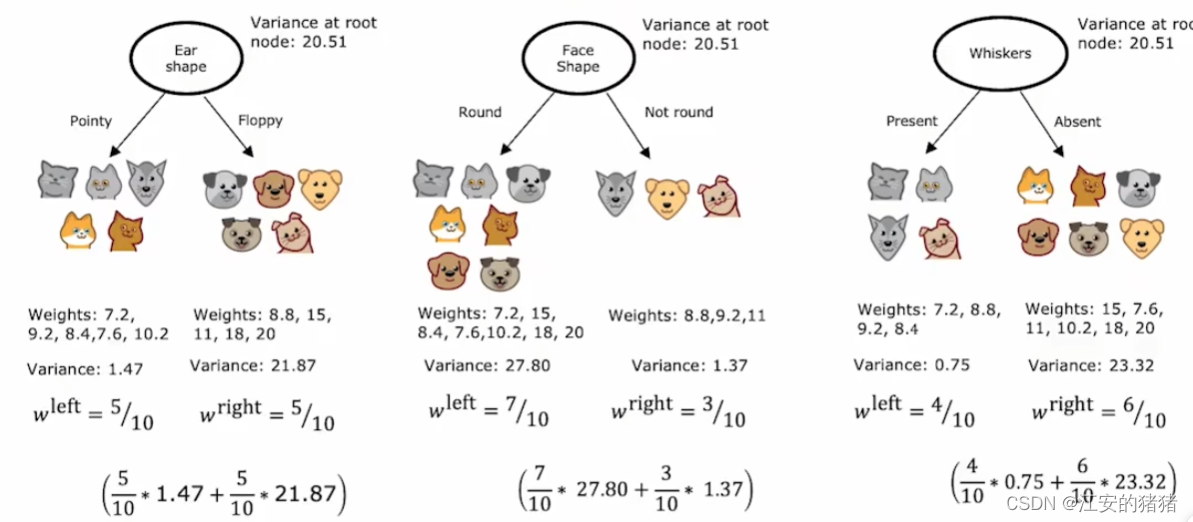
最近3DGS的爆火，引发了一众对三维高斯表达场景的研究。这里的三维高斯是什么？本文用简答的描述和简单实验来呈现三维高斯的数学意义。本文没有公式推导，主打一个意会。

我们高中都学过高斯分布，即一个钟形曲线。它的特点是有一个中心，两边递减。在计算机领域上的优势是：用两个参数$(\mu ,\sigma )$可以表示一个分布。OK，我们继续推广到二维的情况，在CV领域常用一个trick是高斯模糊（即 Gaussian Blur），在关键点的周围模糊一个范围。

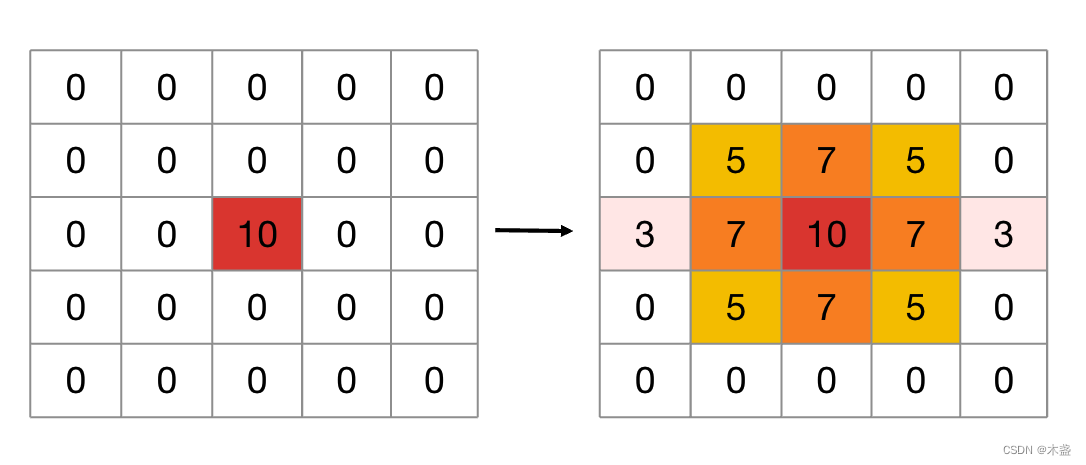
实际上，在关键点的周围模糊出一个范围，这个范围是服从高斯分布的，就像一个钟形曲线的俯视图。这个范围依旧可以用（中心点，协方差）等少数几个参数表示出来。至此，我们可以理解高斯表示的优点之一：用较少的参数可以表示一个任意大小的范围。这一优点特别适合用于场景表示。

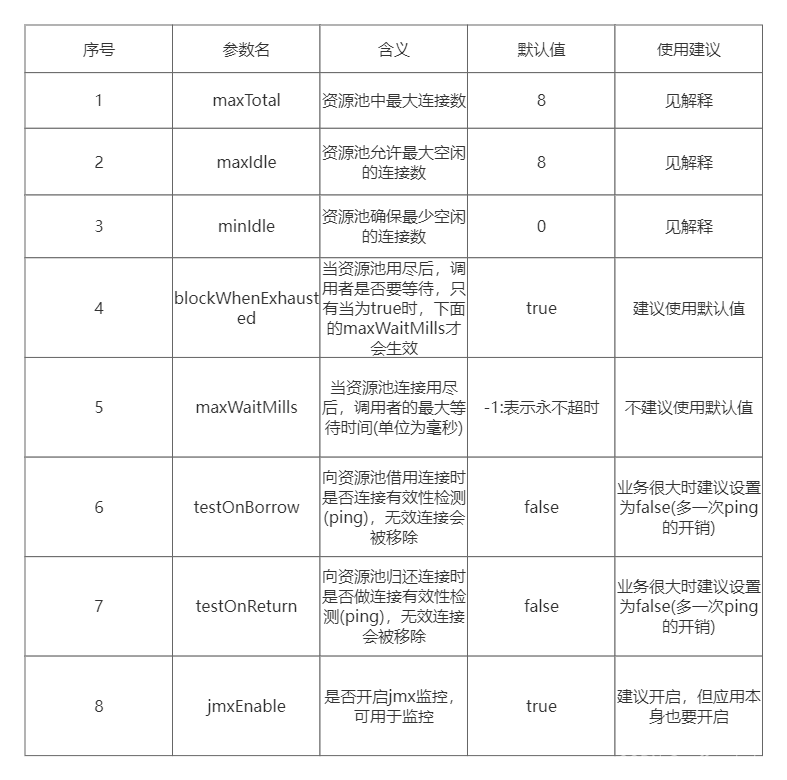
我们将高斯推广到三维——三维高斯。三维高斯在空间中是一个有中心的类椭球物体，3DGS就是用一堆高斯球来表示场景。以3DGS为例，每个三维高斯包含以下参数：

其中，position(x, y, z) 表示三维高斯的中心点，scale和rotation这7个参数表示高斯球的大小和旋转，opacity表示不透明度，SH表示球谐波系数用于进一步的颜色表示。所以，一个朴素三维高斯只需要有（position, scale, rotation）即可，opacity和SH都是3DGS作者为使其更好表达场景而增加的可训练参数。

我们做一个实验，随便初始化三个高斯球，对其（position, scale, rotation）分别设置，默认opacity为1。

xyz = np.array([[-0.7, 0.1, .03],
                [-0.01451855, 0.4050243, -0.11472405],
                [0.30140288, -0.20153112, 0.12868194]])
scales = torch.log(torch.Tensor([0.0428, 0.0836, 0.0711]))[..., None].repeat(1, 3).cuda()
rots = torch.Tensor([0.2, 0.1, 0.2, 0.5])[..., None].repeat(1, 3).cuda()

然后，选取一个合适的相机机位，将这三个高斯球投影到对应视角：

我们可以看到空间中有三个类椭球，这就是我们初始化的高斯球了。在3DGS的训练中，高斯球可以缩放、可以删减，也可以分裂增殖，最终完美重建出一个场景。
我们环绕一圈看一下这三个球的样子：

到这里，应该觉得三维高斯不抽象了吧。
有问题请留言交流～