矢量与矢量场
矢量:又有大小又有方向的量。(力、速度、电场强度等)
矢量场:如果空间中处处都有矢量存在,则称形成了一个矢量场。

表示矢量场的方法:
1、数学表达式:
此表达式为直角坐标系下表达式,其中
分别表示矢量场在x轴,y轴,z轴上的分量
2、图示法:
矢量线:矢量线的切线方向表示场量的方向;矢量线的疏密表示场量的大小。
在直角坐标系中,矢量线的方程可以写为:
通量
设有矢量场
,曲面S
则通量为:
,表示穿过曲面的矢量的代数和。
如果S为闭合曲面,则通量为:
如果通量>0,则说明有正源或正源大于负源;如果通量<0,则说明有负源或负源大于正源;如果通量等于0,则说明无源或正负源相等。
通量可以让我们知道这个曲面上的整体情况,若要问正源或负源是多少、怎样分布无法得出,所以通量是一个宏观量。比如说把教室的门关起来,已知男同学比女同学多5个,问到底有几个男同学、有几个女同学,男女同学怎样分布?无法得出,一种宏观态有无穷多种微观态对应。
矢量场的散度
散度(Divergence)是向量场中的一个重要概念,它描述了向量场在某一点处的“流出”或“流入”的强度。如果把对某点所在的闭合面S压缩,此时通量本身趋近于0,除去S所包围的体积V,取极限得到通量的体密度,即散度。
定义式:
此式表明散度是一个标量,表示从该点单位体积内散发出来的矢量A的通量(即通量密度),反映出矢量场A在该点的强度。
散度计算公式:
为矢量场A在某点(x,y,z)处的散度的计算公式。
证明:从散度的物理意义出发。散度可以理解为单位体积内向量场“流出”或“流入”的净通量。因此,我们可以通过计算一个包含该点的微小体积内的通量变化来近似散度。
考虑一个以点 P(x,y,z) 为中心的小立方体,其边长分别为 Δx,Δy,Δz。向量场 A 在这个立方体上的通量可以通过计算各个面上的通量并求和得到。
对于 x 方向的两个面,通量分别为Ax(x+2Δx,y,z)ΔyΔz 和−Ax(x−2Δx,y,z)ΔyΔz。这两个通量之差除以 ΔxΔyΔz 并取极限 Δx→0,就得到了
。类似地,对于 y 和 z 方向的面,也可以得到
和
。将这三个偏导数相加,就得到了散度的计算公式。
物理意义:

散度可以表示为哈密顿算子与矢量A的点乘:
由计算公式可得:
散度运算符合下列规则:
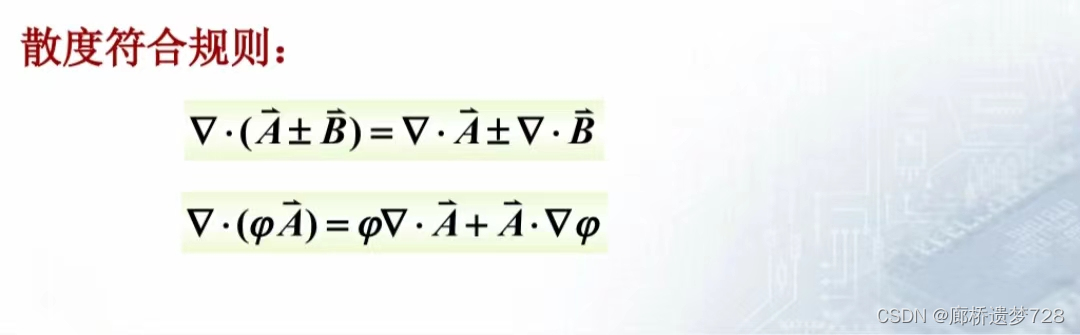
高斯散度定理

将闭合曲面S围成的体积V分成许多体积元,计算每个体积元的小封闭曲面S上穿过的通量,然后叠加。其总和刚好等于从封闭曲线S穿出来的通量。