在操作之前需要先下载Julia的Distributions包，这个包用于进行相关概率分布的函数调用。

在输入 ] 进入Julia包管理模式后输入：

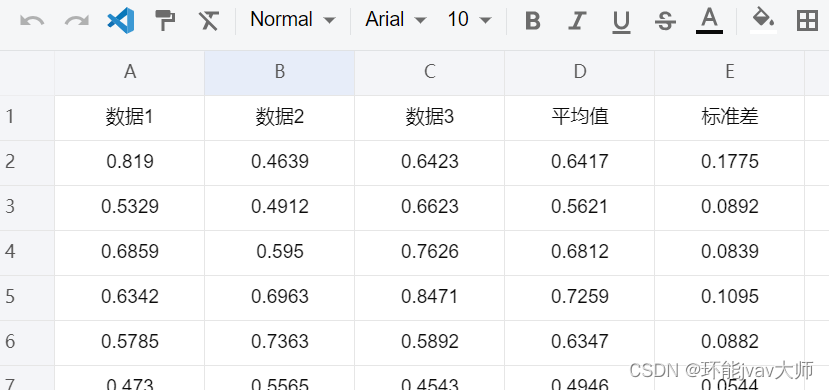
add Distributions

这里我使用我们自己实验室的实测数据 ，平均值=0.67，方差=0.11，数据分布服从于正态分布，使用 Normal() 函数：

d = Normal(0.67, 0.11) 

测试次数为3次一组，属于小样本量，所以使用 n-1 作为分母来得到无偏估计 

#平均值
average = (data1 + data2 + data3) / 3
#标准差(无偏样本标准差，分母为 n-1)
standard_deviation = sqrt(((data1 - average)^2 + (data2 - average)^2 + (data3 - average)^2) / 2)

完整版Julia代码

using Distributions  
  
# 创建一个均值为 0.67，标准差为 0.11 的正态分布对象  
d = Normal(0.67, 0.11)  
  
# 指定要生成的行数  
num_rows = 10 
  
open("BBGoy.csv", "w") do file   
    write(file, "数据1,数据2,数据3,平均值,标准差\n")  
       
    for i = 1:num_rows  
        # 从指定的正态分布中随机生成三个样本  
        data1 = rand(d)  
        data2 = rand(d)  
        data3 = rand(d)  
          
        # 平均值  
        average = (data1 + data2 + data3) / 3  
          
        # 标准差（无偏样本标准差，分母为 n-1）  
        standard_deviation = sqrt(((data1 - average)^2 + (data2 - average)^2 + (data3 - average)^2) / 2)  
           
        csv_row_data = [data1, data2, data3, average, standard_deviation]  
        formatted_csv_row = join(map(x -> "$(round(x, digits=4))", csv_row_data), ",")  
        write(file, formatted_csv_row * "\n")  
    end  
end

R语言代码

#设置随机数种子 
set.seed(123)  

# 均值为 0.67，标准差为 0.11 的正态分布 
mu <- 0.67  
sigma <- 0.11  

num_rows <- 10  

results <- data.frame(数据1 = numeric(num_rows),  
                      数据2 = numeric(num_rows),  
                      数据3 = numeric(num_rows),  
                      平均值 = numeric(num_rows),  
                      标准差 = numeric(num_rows))  

for (i in 1:num_rows) {  
  data1 <- rnorm(1, mean = mu, sd = sigma)  
  data2 <- rnorm(1, mean = mu, sd = sigma)  
  data3 <- rnorm(1, mean = mu, sd = sigma)  
  
  average <- (data1 + data2 + data3) / 3  
  
  # 小样本量通常使用 n-1 作为分母来得到无偏估计  
  n <- 3  
  variance <- ((data1 - average)^2 + 
                 (data2 - average)^2 + (data3 - average)^2) / (n - 1) 
  
  standard_deviation <- sqrt(variance)  
  results[i, ] <- c(data1, data2, data3, average, standard_deviation)  
}  

# 保留四位小数  
formatted_results <- data.frame(lapply(results, function(x) 
  format(x, digits = 4, nsmall = 4)))  
 
write.table(formatted_results, file = "BBGoy.csv", 
            row.names = FALSE, col.names = TRUE, sep = ",", quote = FALSE)

生成数据