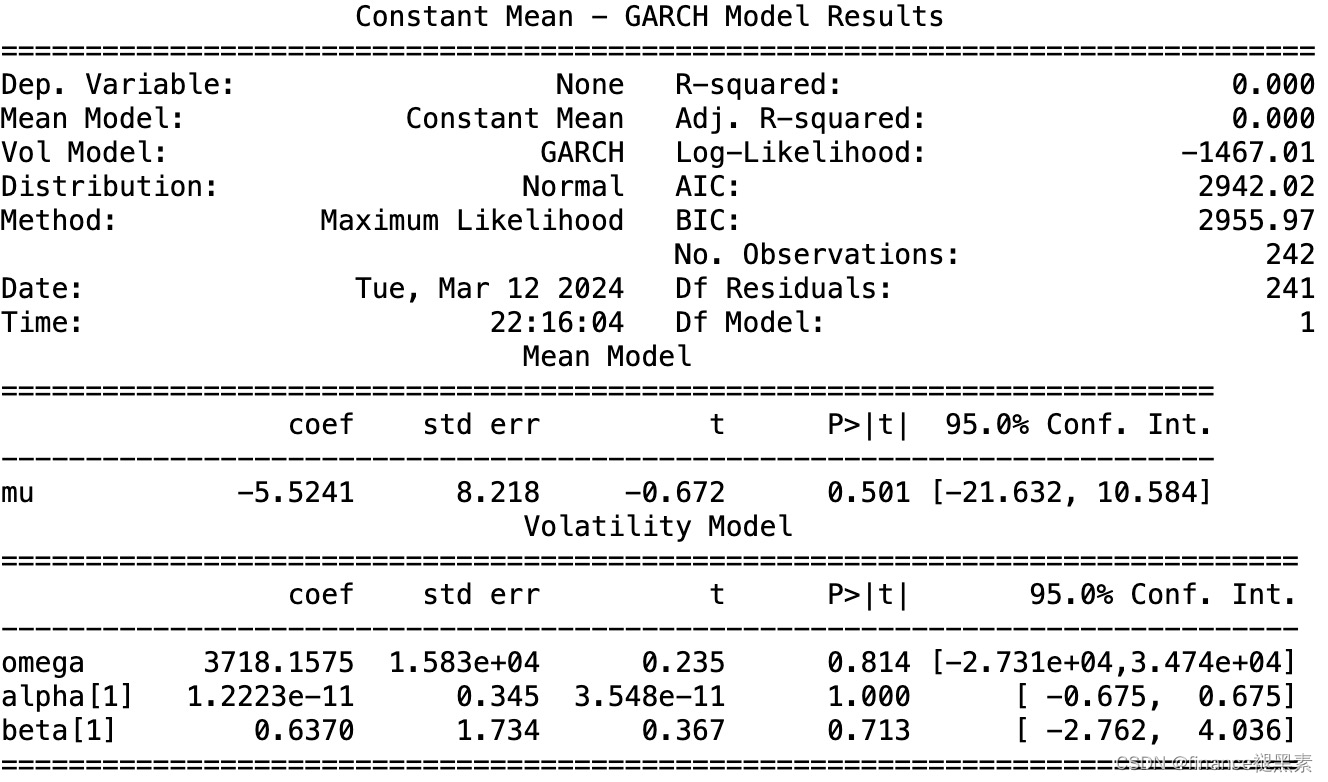
还记得我在【机器学习300问】的第28问里谈到的,看决策树的定义不就是if-else语句吗怎么被称为机器学习模型?其中最重要的两点就是决策树算法要能够自己回答下面两问题:
- 该选哪些特征 == 特征选择
- 该选哪个阈值 == 阈值确定
今天这篇文章承接上文,继续深入的讲讲决策树是如何进行特征选择的?如果没有看上篇文章的友友可以点个链接哦:
【机器学习300问】28、什么是决策树?![]() http://t.csdnimg.cn/Tybfj
http://t.csdnimg.cn/Tybfj
一、看一个猫咪二分类的例子
假设你正在教一群小朋友在公园里快速分辨出哪些动物是猫,哪些是狗。现在你们面前有一大堆动物的照片,每张照片都包含了三个特征,比如“耳朵形状”、“脸是不是圆的”、“有没有胡须”。让我们试着用决策树算法来构造一颗树,先只构造根节点和左右子树。
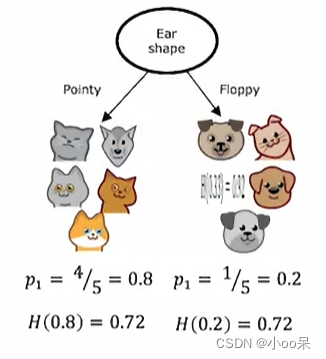
选择耳朵是竖起来还是塌下去这个特征,我们把10个样本分成了两个子树。图中p代表猫猫出现的概率(或占比),H是信息熵函数。
二、什么是信息熵?
首先,我们得理解信息熵的概念,信息熵是衡量一个随机变量不确定性的度量。就像孩子们开始时对所有照片的不确定性。如果照片中猫和狗的数量各占一半,那么不确定性最高,就好比每个小朋友随机猜的话,正确率只有50%。这个不确定性可以用数学上的熵来量化:
其中 表示数据集,
是类别
出现的概率。如果还是有点困惑的话,我们画一个图并配合一些例子来进一步解释信息熵的概念。
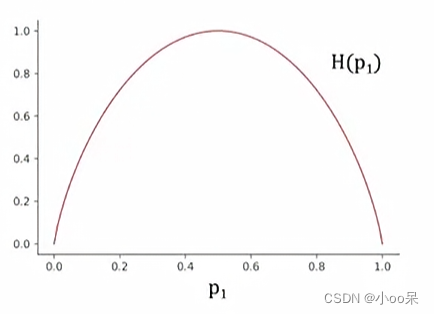
(1)p=0.5 H=1的情况
这张图是信息熵的曲线图,可以看到在p=0.5的时候,信息熵最大意味着此时对于这张图片是猫咪还是小狗最不确定。也就是说是猫的可能性为50%,是狗的可能性也是50%
(2)p=0.83 H=0.65的情况
假设p=0.83图中可以看出H(0.8)=0.65,这种情况是说,6个动物图片中有5个是小猫1个是小狗,那么我比较有把握的说和这6张图片类似的动物图片,我蛮确定它是小猫,有多确定它是小猫呢?有0.65的确定性。
(3)p=1 H=0的情况
假设p=1,从图中可以看出H=0,这种情况是说按照某种特征来区分猫狗,分出来一边全是猫咪,一边全是小狗,这意味着数据集中的不确定性最小(不确定性为零)
(4)总结一下什么是信息熵
- 信息熵是衡量一个随机变量不确定性的度量
- 当某个事件发生完全确定时(概率为1或0),信息熵为0
- 当事件发生的不确定性最高,所有可能结果的概率相同时,对于二元事件(如猫狗分类),信息熵达到最大值1
三、什么是信息增益?
简单说信息增益就是划分前的信息熵减去条件熵,表示使用该特征后不确定性减少的程度。
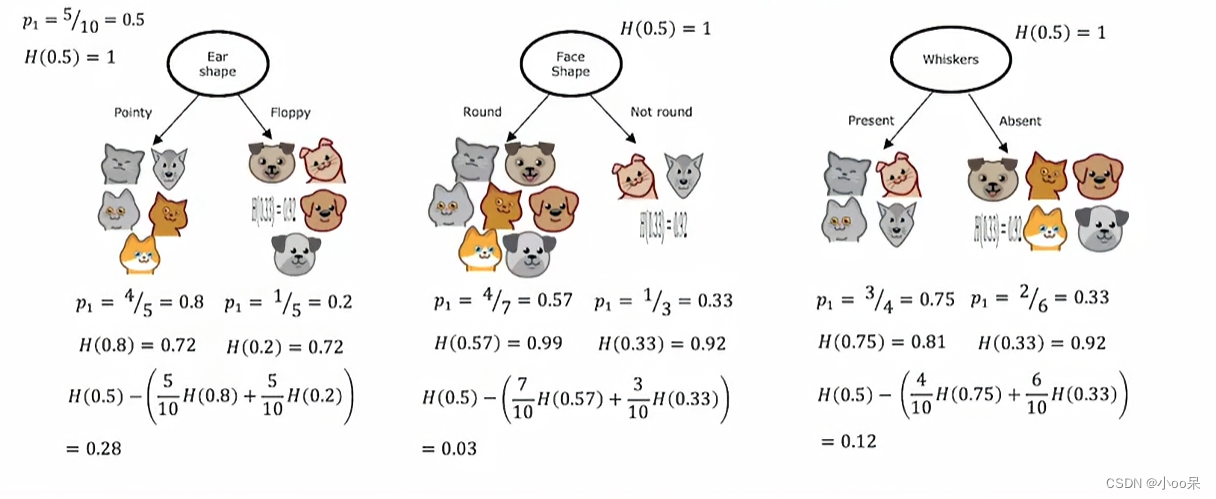
(1)加权平均信息熵
在图3中,用耳朵的形状进行划分后,左右两个子树的信息熵可以单独被计算出来,一个是H(0.8)=0.72另一个是H(0.2)=0.72,这两个数代表了两个子树他们的不确定性,可是我现在想知道的是用耳朵的形状进行划分这种策略所到账的不确定性。所以我可以使用加权平均的方法将左右两个合在一起计算得到这种特征用于根节点决策所导致不确定性:
其中的就是权重,w具体是指子树的样本数量占总样本数量的比例,p具体是指猫出现在子树中的概率。这样我们就得到了采取某种特征进行分类的策略会导致多少不确定性。才能判断出这个特征选的好不好。
(2)信息增益公式
但这还不够,因为我们要思考这个策略好不好,主要不是看当下的H值,而是看他相较于上一次减少了多少不确定性,这样做更有利于我们判断到底选哪个特征做根节点好,所以我们得用前一次的不确定性减去这一次的不确定性,得出来的就是信息增益(根节点):
写成更一般(任意决策节点)的公式就是:
| 符号 | 含义 |
| 表示在给定特征 f 的条件下,数据集D的信息增益 | |
| 数据集的原始信息熵 | |
| 子集大小占总数据集大小的比例 | |
| 子集的信息熵 |
四、决策树是如何进行特征选择的?
具体选择的流程:
- 计算划分前的数据集熵(即原始不确定性)。
- 对于每一个特征,比如“耳朵形状”,按照这个特征把数据集划分为不同的子集。
- 分别计算每个子集的信息熵,并根据子集内样本数目的比例加权求和。
- 计算出信息增益,信息增益就是划分前的熵减去条件熵,表示使用该特征后不确定性减少的程度。
- 对比每一个特征计算出来的信息增益,选择那个信息增益最大的特征!