三个关键要素
- 从相机配准的过程中得到的稀疏点云开始,使用3D Gaussian表示场景; 3D Gaussian: 是连续体积辐射场能够防止不必要的空空间优化。
- 对 3D Gaussion进行交叉优化和密度控制: 优化各向异性血方差对场景精确表示。
- 使用快速可视感知渲染算法来进行快速的训练和渲染。

Differentiable 3D Gaussian Splitting
- 表示方法和[1][2]有相似性,同时假设每一个点有一个带法线的平面圆。
- 由于SFM得到的点非常稀疏,很难估计法线,因此,我们建模我们的几何结构为一组不需要法线的3D高斯。定义为一个定义在世界空间的全3D协方差矩阵(3D coveriance matrix)
Σ
\Sigma
Σ,中心在点
μ
\mu
μ(mean):
G ( x ) = e − 1 2 ( x ) T Σ − 1 ( x ) G(x) = e^{- \frac{1}{2}(x)^T\Sigma^{-1}(x)} G(x)=e−21(x)TΣ−1(x) - 我们为了渲染需要将3D高斯投影到2D。给一个视角转换W,对应的在相机坐标系下协方差矩阵
Σ
′
\Sigma'
Σ′为:
Σ ′ = J W Σ W T J T \Sigma' = JW\Sigma W^TJ^T Σ′=JWΣWTJT, J是投影变换的仿射近似雅可比矩阵。 - 直观的想法是直接优化协方差矩阵
Σ
\Sigma
Σ获得3D高斯代表辐射场。但是,协方差矩阵只有在半正定时才有物理意义。
协方差矩阵的物理意义在于它反映了变量之间的关联程度。如果协方差矩阵是半正定的,这意味着其中任何一个向量与自身的内积(即方差)都是非负的。这种情况下,变量之间的关系是一种相对“稳定”的关系,其中一个变量的增加往往会伴随着另一个变量的增加或减少,而且这种关系的变化程度是可控的。
- 所以我们选择把协方差矩阵等效为一个椭球的构型。给出尺度矩阵S和旋转矩阵R,我们可以找到 Σ = R S S T R T \Sigma = RSS^TR^T Σ=RSSTRT.
- 为了能够独立优化这些参数,我们将其分开存储:一个3D向量s表示尺度,一个四元数q表示旋转。
Optimization with Adaptive Density Control of 3D Gaussians
- 除了位置p, α \alpha α和协方差 Σ \Sigma Σ以外,我们还优化每个高斯颜色c的SH系数。
Optimization
- 该优化是基于连续的渲染迭代,并将生成的图像与捕获的数据集中的训练视图进行比较。
- 由于几何可能被不正确地从2D到3D预测,所以优化过程需要对几何进行创造或毁灭。
- 我们将初始协方差矩阵(initial covariance matrix)估计为各向同性(isotropic)高斯矩阵,其轴等于到最近三个点的距离的平均值。
Adaptive Control of Gaussians
- 我们从SfM的初始化稀疏点开始,应用我们的方法自适应控制单位体积上高斯的数量和密度。优化预热后,每100次迭代进行一次致密化,删除任何本质上透明( α \alpha α小于阈值)的高斯分布。
- 我们对高斯的自适应控制需要填充空白区域。 它重点关注缺少几何特征的区域(“under-Reconstruction”),但也关注高斯覆盖场景中大面积的区域(“over-reconstruction”)。 我们观察到两者都有很大的视图空间位置梯度( large view-space positional gradients)。 直观上,这可能是因为它们对应于尚未很好重建的区域,并且优化尝试移动高斯来纠正这一点。
- 两种情况都是致密化的候选。我们用视野空间位置梯度(view-space position
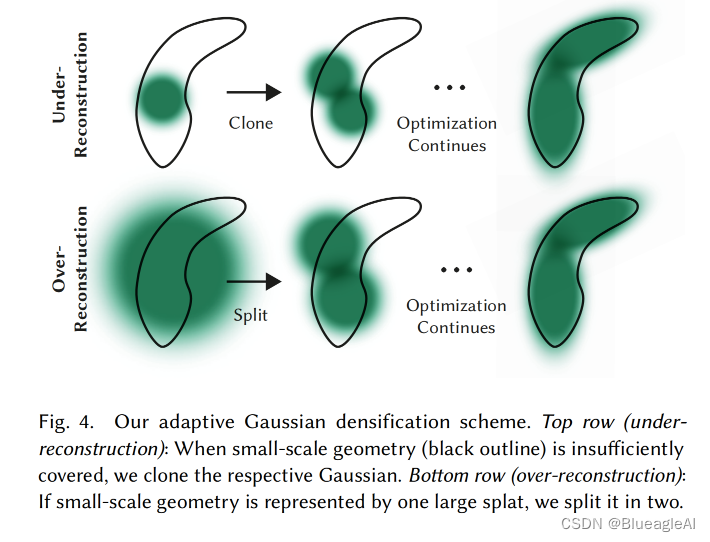
gradients)的平均幅度超过高斯 τ p o s \tau_{pos} τpos,在我们的测试中将其设置为0.0002。 - Under Reconstruction: 对于重建区域中的小高斯,我们需要覆盖必须创建的新几何形状。 为此,最好通过简单地创建相同大小的副本并将其沿位置梯度的方向移动来克隆高斯。
- Over Reconstruction 具有高方差的区域中的大高斯需要被分割成更小的高斯。 我们用两个新的高斯函数替换这些高斯函数,并将它们的尺度除以我们通过实验确定的系数
ϕ
\phi
ϕ = 1.6。 我们还通过使用原始 3D 高斯作为 PDF 进行采样来初始化它们的位置。
- 与其他体积表示类似,我们的优化可能会被靠近输入摄像机的漂浮物卡住;在我们的例子中,这可能会导致高斯密度的不合理的增加。
- 解决这个问题的有效方法是每N = 3000次迭代后将 α \alpha α设为接近0。然后增加 α \alpha α,开始剔除透明的高斯。
Fast Differentiable Rasterizer(栅格化) for Gaussians
- 我们的目标是有快速的整体渲染和快速的排序,以允许近似的𝛼混合( α \alpha α-blending)(包括各向异性飞溅),并防止硬限制能收到梯度的飞溅数量。
- 为了达成目标,我们设计了一个基于图块的高斯溅射光栅器。其灵感来自最近的软件光栅化方法,一次对整个图像进行预排序图元,避免了阻碍以前 α \alpha α-blending解决方案的每个像素排序的花费。
- 我们的方法首先将幕布溅射成 16 × 16 16\times16 16×16的块,然后继续针对视锥体和每个图块剔除 3D 高。具体来说,我们只保留与视锥体相交的置信区间为 99% 的高斯分布。
- 此外,我们使用保护带来简单地拒绝极端位置处的高斯分布(即均值接近近平面且远离视锥体的位置),因为计算它们的投影 2D 协方差将不稳定。
- 然后,我们根据重叠的图块数量实例化每个高斯,并为每个实例分配一个结合视图空间深度和图块 ID 的键。
- 然后,我们使用单个快速 GPU 基数排序根据这些键对高斯进行排序。
- 然而,当图块接近单个像素的大小时,这些近似值变得可以忽略不计。 我们发现这种选择极大地增强了训练和渲染性能,而不会在融合场景中产生可见的伪影。
- 对高斯进行排序后,我们通过识别第一个和最后一个映射到给定图块的深度(depth)排序条目来为每个图块生成一个列表。 对于光栅化,我们为每个图块启动一个线程块。 每个块首先协作地将高斯数据包加载到共享内存中,然后对于给定的像素,通过从前到后遍历列表来累积颜色和𝛼值,从而最大化数据加载/共享和处理的并行性增益。 当我们达到像素中的目标饱和度(saturation) 𝛼 时,相应的线程就会停止。 每隔一段时间,就会查询图块中的线程,并且当所有像素都饱和时(即 𝛼 变为 1),整个图块的处理就会终止。
- 在光栅化过程中,𝛼的饱和度是唯一的停止标准。 与之前的工作相比,我们不限制接收梯度更新的混合基元的数量。 我们强制执行此属性,以允许我们的方法处理具有任意、不同深度复杂性的场景并准确地学习它们,而不必求助于特定于场景的超参数调整。 因此,在后向传递过程中,我们必须恢复前向传递中每个像素的混合点的完整序列。 一种解决方案是将每个像素的任意长混合点列表存储在全局内存中[Kopanas et al. 2021]。 为了避免隐含的动态内存管理开销,我们选择再次遍历每个图块列表; 我们可以重用前向传递中的高斯排序数组和平铺范围。 为了便于梯度计算,我们现在从后到前遍历它们。
- 遍历从影响图块中任何像素的最后一个点开始,并且将点加载到共享内存中再次协作发生。 此外,如果每个像素的深度低于或等于前向传递过程中对其颜色有贡献的最后一个点的深度,则每个像素只会开始(昂贵的)点重叠测试和处理。 第 2 节中描述的梯度计算。 4 需要原始混合过程中每个步骤的累积不透明度值。 我们可以通过在前向传递结束时仅存储累积的总不透明度来恢复这些中间不透明度,而不是在后向传递中遍历逐渐缩小的不透明度的显式列表。 具体来说,每个点存储的是前向过程中最终累积的不透明度𝛼; 我们在从后到前的遍历中将其除以每个点的𝛼,以获得梯度计算所需的系数。
Reference
[1] Georgios Kopanas, Julien Philip, Thomas Leimkühler, and George Drettakis. 2021. Point-Based Neural Rendering with Per-View Optimization. Computer Graphics Forum 40, 4 (2021), 29–43. https://doi.org/10.1111/cgf.14339.
[2] Wang Yifan, Felice Serena, Shihao Wu, Cengiz Öztireli, and Olga Sorkine-Hornung.
2019. Differentiable surface splatting for point-based geometry processing. ACM
Transactions on Graphics (TOG) 38, 6 (2019), 1–14.