目录
- 1. 模型定义
- 1.1 ARMA-GARCH模型
- 1.2 引入节假日效应的虚拟变量的新模型
- 1.3 引入日历效应的虚拟变量的新模型
- 2. 实证部分
- 2.1 准备工作
- 2.2 引入节假日效应虚拟变量的模型建立和结果分析
- 2.3 引入节假日效应和日历效应的虚拟变量的模型建立和结果分析
- 3. 结语
本文介绍了ARMA-GARCH模型的基本定义和构建方式。随后,提出了引入节假日效应和日历效应的虚拟变量的模型定义,并根据定义进行了建模和结果分析。包含代码和结果展示。包含数据、代码的文件可关注gzh‘finance褪黑素’,在gzh下回复关键词【20240312】获取。更多金融大数据的内容可关注博主。
1. 模型定义
股票数据常常表现出波动性聚焦的特征,选择ARMA-GARCH模型能够捕捉时间序列的波动性,并且能够根据过去的波动性估计未来的波动性,预测效果很优秀,所以这里选择这个模型来拟合深证综指的收盘价数据。
1.1 ARMA-GARCH模型
ARMA-GARCH模型是ARMA模型和GARCH模型的组合,分别包含两个公式,一个是ARMA模型的均值方程,一个是GARCH模型的方差方程,它们组合时首先利用均值方程对收益率进行建模,然后对建模后的残差利用方差方程进一步计算,得到最终的组合模型。以下是ARMA-GARCH模型的基本公式:
-
ARMA模型(均值方程):
Y t = μ + ϕ 1 Y t − 1 + ϕ 2 Y t − 2 + … + ϕ p Y t − p + ε t − θ 1 ε t − 1 − θ 2 ε t − 2 − … − θ q ε t − q \ Y_t = \mu + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \ldots + \phi_p Y_{t-p} + \varepsilon_t - \theta_1 \varepsilon_{t-1} - \theta_2 \varepsilon_{t-2} - \ldots - \theta_q \varepsilon_{t-q}\ Yt=μ+ϕ1Yt−1+ϕ2Yt−2+…+ϕpYt−p+εt−θ1εt−1−θ2εt−2−…−θqεt−q
μ \mu μ是常数项, ϕ i \phi_i ϕi 是自回归系数, θ i \theta_i θi 是移动平均系数, ε t \varepsilon_t εt是白噪声项(均值为0),方差为 σ t 2 \sigma_t^2 σt2。 -
GARCH模型(方差方程):
σ t 2 = α 0 + α 1 ε t − 1 2 + α 2 ε t − 2 2 + … + α p ε t − p 2 + β 1 σ t − 1 2 + β 2 σ t − 2 2 + … + β q σ t − q 2 \sigma_t^2 = \alpha_0 + \alpha_1 \varepsilon_{t-1}^2 + \alpha_2 \varepsilon_{t-2}^2 + \ldots + \alpha_p \varepsilon_{t-p}^2 + \beta_1 \sigma_{t-1}^2 + \beta_2 \sigma_{t-2}^2 + \ldots + \beta_q \sigma_{t-q}^2\ σt2=α0+α1εt−12+α2εt−22+…+αpεt−p2+β1σt−12+β2σt−22+…+βqσt−q2
其中, σ t 2 \sigma_t^2 σt2 是条件方差, α i \alpha_i αi 是平方项的ARCH系数, β i \beta_i βi是条件方差项的GARCH系数。
整个ARMA-GARCH模型的形式是将均值方程和方差方程结合起来。可以表示为:
Y
t
=
μ
+
ϕ
1
Y
t
−
1
+
ϕ
2
Y
t
−
2
+
…
+
ϕ
p
Y
t
−
p
+
ε
t
−
θ
1
ε
t
−
1
−
θ
2
ε
t
−
2
−
…
−
θ
q
ε
t
−
q
\ Y_t = \mu + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \ldots + \phi_p Y_{t-p} + \varepsilon_t - \theta_1 \varepsilon_{t-1} - \theta_2 \varepsilon_{t-2} - \ldots - \theta_q \varepsilon_{t-q}\
Yt=μ+ϕ1Yt−1+ϕ2Yt−2+…+ϕpYt−p+εt−θ1εt−1−θ2εt−2−…−θqεt−q
s
i
g
m
a
t
2
=
α
0
+
α
1
ε
t
−
1
2
+
α
2
ε
t
−
2
2
+
…
+
α
p
ε
t
−
p
2
+
β
1
σ
t
−
1
2
+
β
2
σ
t
−
2
2
+
…
+
β
q
σ
t
−
q
2
\ sigma_t^2 = \alpha_0 + \alpha_1 \varepsilon_{t-1}^2 + \alpha_2 \varepsilon_{t-2}^2 + \ldots + \alpha_p \varepsilon_{t-p}^2 + \beta_1 \sigma_{t-1}^2 + \beta_2 \sigma_{t-2}^2 + \ldots + \beta_q \sigma_{t-q}^2\
sigmat2=α0+α1εt−12+α2εt−22+…+αpεt−p2+β1σt−12+β2σt−22+…+βqσt−q2
最终得到的模型可以用于对未来值的预测和波动性的估计。
1.2 引入节假日效应的虚拟变量的新模型
在均值模型的基础上,加入新的虚拟变量,代表日历效应或节假日效应,将虚拟变量乘以一个系数,然后将其添加到均值方程的常数项上。
例如,假设虚拟变量为
D
t
\ D_t
Dt,表示第t个观测是否处于节前,处于节前为1,处于节后为0,来探究节前效应。
一般认为节前和节后具有不同的效应,需要分开进行对比,因此赋予虚拟变量不同的值可以检验节前和节后,比如检验节前效应时,对节日前的日期赋予 D t \ D_t Dt为1,节日后的日期赋予 D t \ D_t Dt为0,而在检验节后效应时,可以对节日前的日期赋予 D t \ D_t Dt为0,对节日后的赋予 D t \ D_t Dt为1.本文探讨的是节前效应,下文会附带代码,需要检验节后效应可以在作者指定的位置修改即可。
加入节日效应的虚拟变量后的均值方程可以表示为:
Y
t
=
μ
+
β
D
t
+
ϕ
1
Y
t
−
1
+
ϕ
2
Y
t
−
2
+
…
+
ϕ
p
Y
t
−
p
+
ε
t
−
θ
1
ε
t
−
1
−
θ
2
ε
t
−
2
−
…
−
θ
q
ε
t
−
q
\ Y_t = \mu + \beta D_t + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \ldots + \phi_p Y_{t-p} + \varepsilon_t - \theta_1 \varepsilon_{t-1} - \theta_2 \varepsilon_{t-2} - \ldots - \theta_q \varepsilon_{t-q}\
Yt=μ+βDt+ϕ1Yt−1+ϕ2Yt−2+…+ϕpYt−p+εt−θ1εt−1−θ2εt−2−…−θqεt−q
其中:
- Y t \ Y_t Yt 是时间序列的观测值。
- μ \mu μ 是常数项。
- D t D_t Dt 是虚拟变量,表示在时间 (t) 是否存在某个效应。
- β \beta β 是虚拟变量的系数。
- ϕ 1 , ϕ 2 , … , ϕ p \phi_1, \phi_2, \ldots, \phi_p ϕ1,ϕ2,…,ϕp 是自回归项的系数。
- ε t \varepsilon_t εt 是白噪声项。
- θ 1 , θ 2 , … , θ q \theta_1, \theta_2, \ldots, \theta_q θ1,θ2,…,θq 是移动平均项的系数。
1.3 引入日历效应的虚拟变量的新模型
同样的,仿照上面节假日效应的检验思路,如果需要探究日历效应的影响,那么可以引入日历效应的虚拟变量的新模型。类似
D
t
D_t
Dt,可以令
K
t
K_t
Kt为新的虚拟变量,对月份结束前的日期赋予
K
t
\ K_t
Kt为1,月份结束后的日期赋予
K
t
\ K_t
Kt为0。
方程和上面的一样。
在某些时候,不能单独考虑节假日效应或是日历效应的影响,因为某些日期重合,发生影响的部分可能是另一种效应,因此最好是添加两个效应的虚拟变量一同列举模型,只有在参数都显著的情况下,才能确定存在该效应。比方说前文只探究了节假日效应,就不能完全确定这是由节假日引起的,参数的显著可能是因为日历效应,所以当引入两个虚拟变量,且在这种时候节假日效应的虚拟变量参数显著时,才能说存在节假日效应。
下面会列举如何在模型中添加一个和两个虚拟变量。
2. 实证部分
2.1 准备工作
首先导入股票数据:
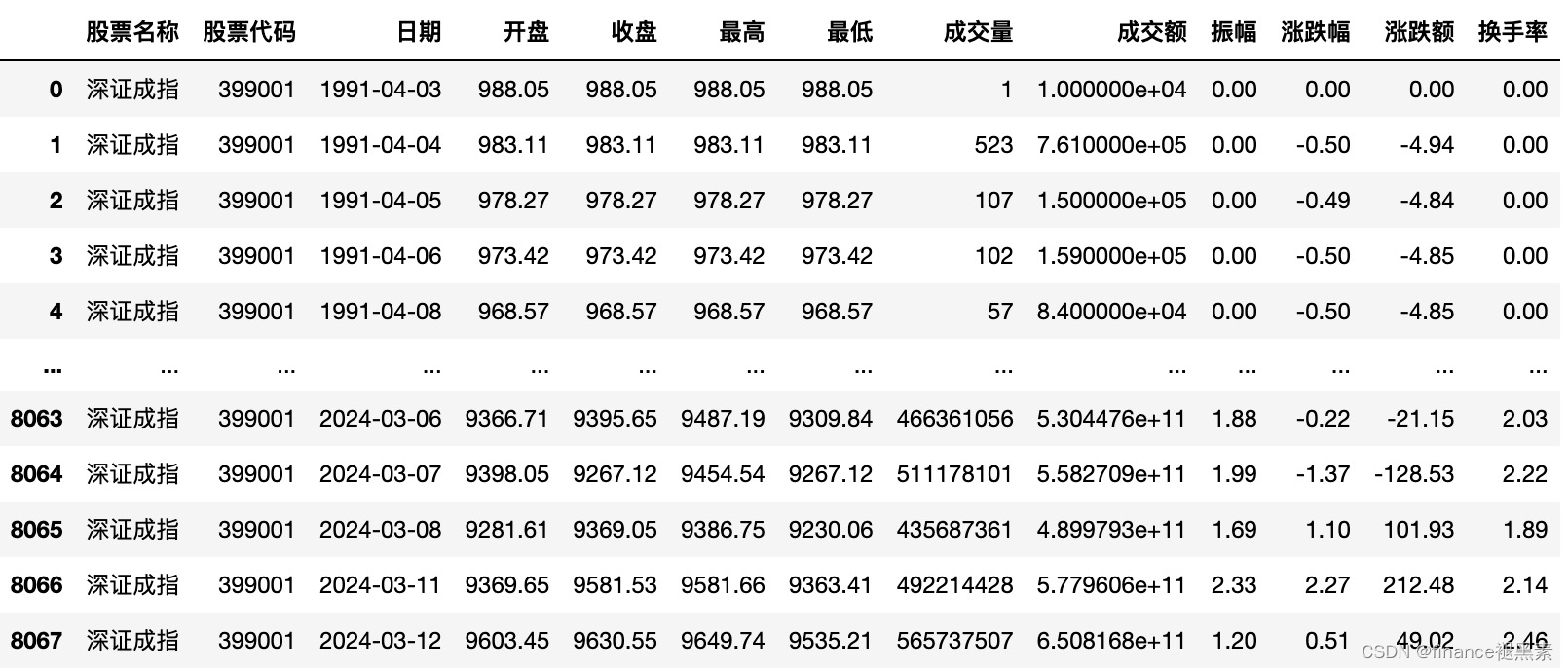
本文实证部分针对2023年一年的数据进行研究。
对股价收盘价做趋势图,标注出几个重要节日的日期:
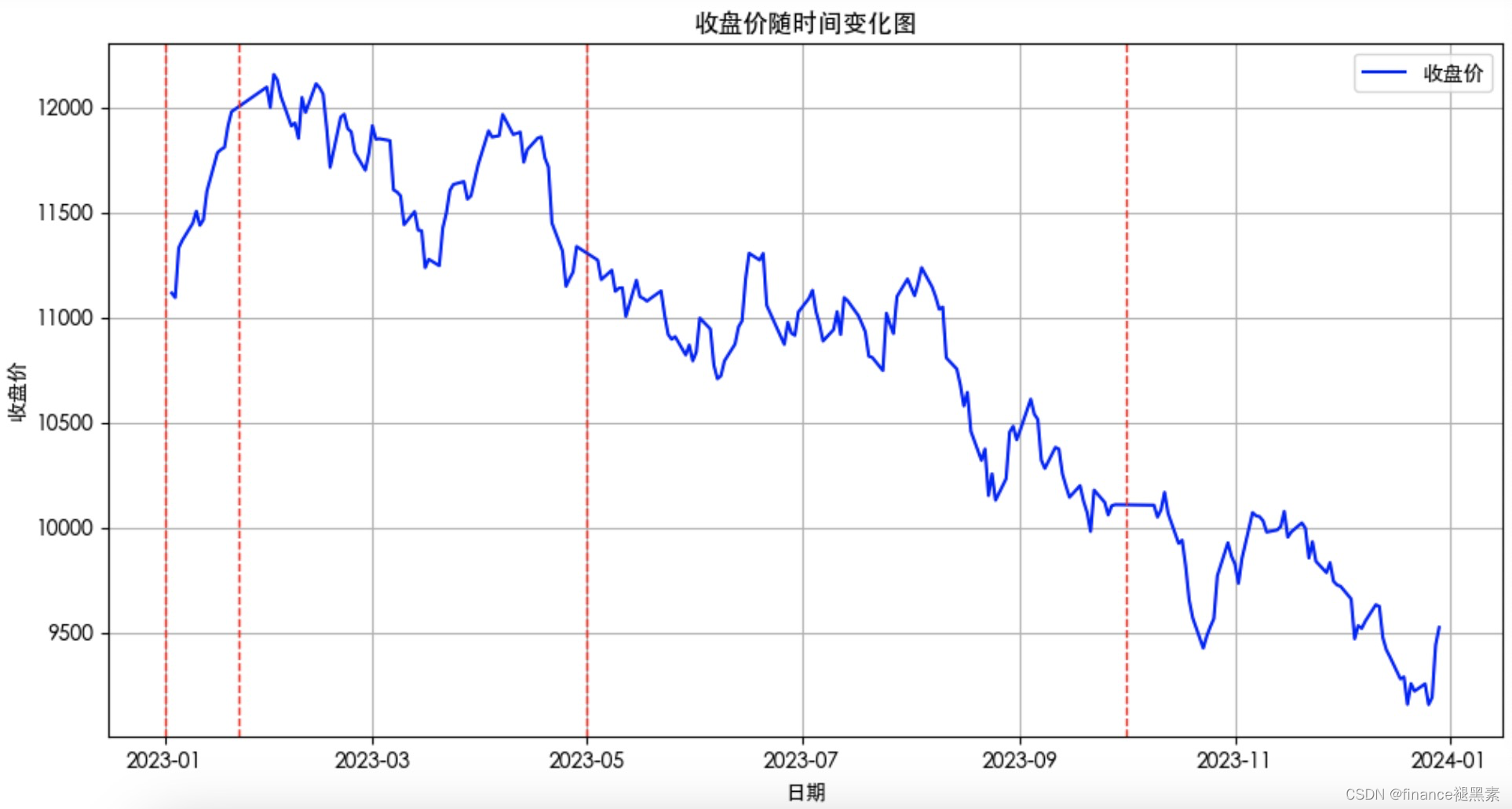
看了一些文献,还可以计算不同节日前节日后股价的收盘价平均值、方差、波动性等进行对比,此处没有计算,直接进入实证模型。
计算2023年春节节前效应的虚拟变量:(如果是节后效应,将第二行和第四行的0改为1即可,代码比较简单)
before_date = '2023-01-22'
df['新列'] = 0
df.loc[df['日期'] < pd.to_datetime(before_date), '新列'] = 1
before_df = df[df['新列'] == 0]
2.2 引入节假日效应虚拟变量的模型建立和结果分析
from statsmodels.tsa.arima.model import ARIMA
from arch import arch_model
arma_model = ARIMA(df['收盘'], order=(1, 0, 1), exog=df['新列'])
arma_result = arma_model.fit()
print(arma_result.summary())
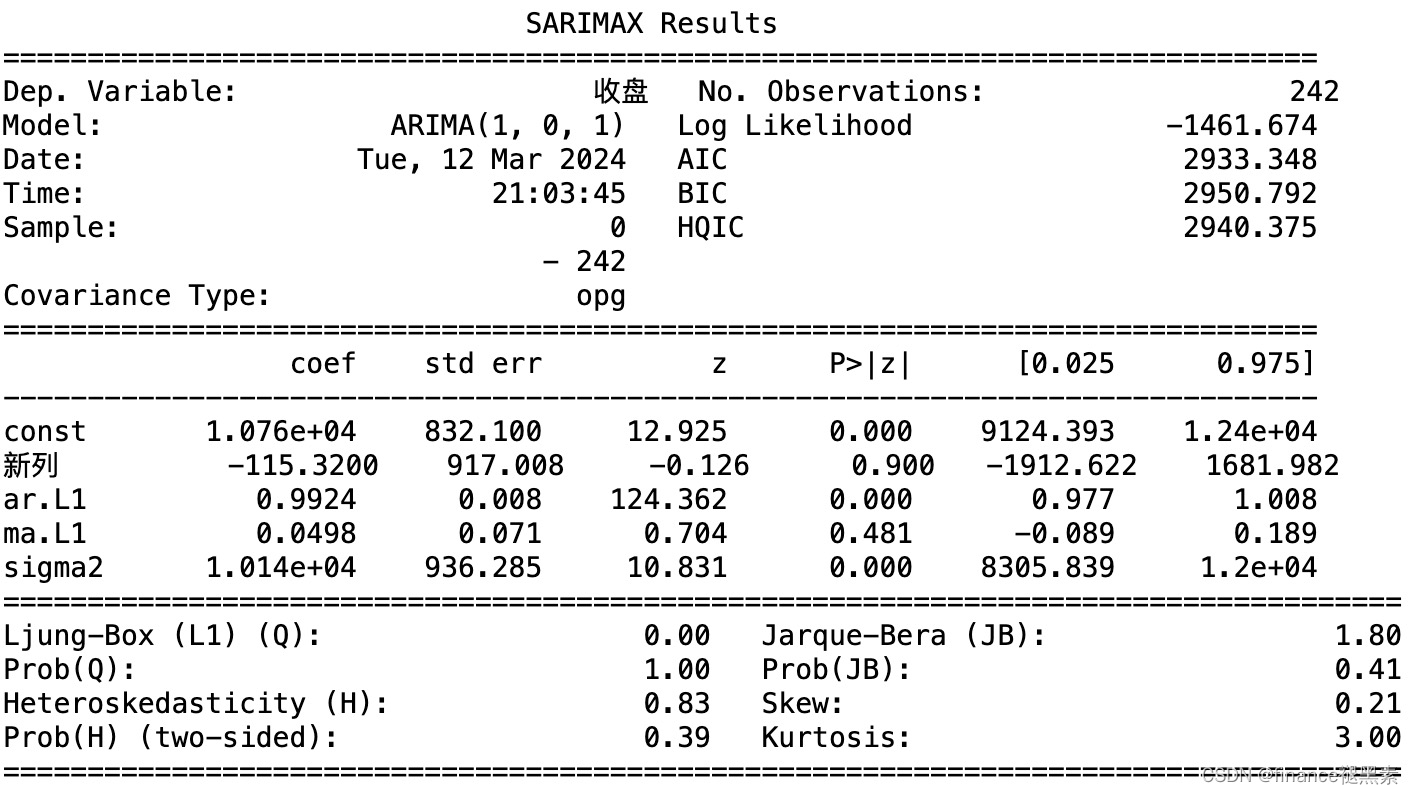
解释结果:
新列 (虚拟变量): 虚拟变量的系数。在这个例子中,虚拟变量的系数为-115.3200。由于该系数的P值很大(0.900),说明虚拟变量的系数不显著,可能不具备统计学意义,说明2023年春节对该年收益变动不具有节假日效应。
ar.L1 (自回归项): ARIMA模型中的自回归项的系数。在这个例子中,自回归项的系数为0.9924。由于P值很小(0.000),我们可以拒绝虚无假设,说明该自回归项是显著的。
ma.L1 (滑动平均项): ARIMA模型中的滑动平均项的系数。在这个例子中,滑动平均项的系数为0.0498。由于P值较大(0.481),我们不能拒绝虚无假设,说明该滑动平均项可能不显著。
对上面的均值方程的结果提取出resid代入方差方程,也就是garch模型:
garch_model = arch_model(arma_result.resid, vol='Garch', p=1, q=1)
garch_result = garch_model.fit()
print(garch_result.summary())
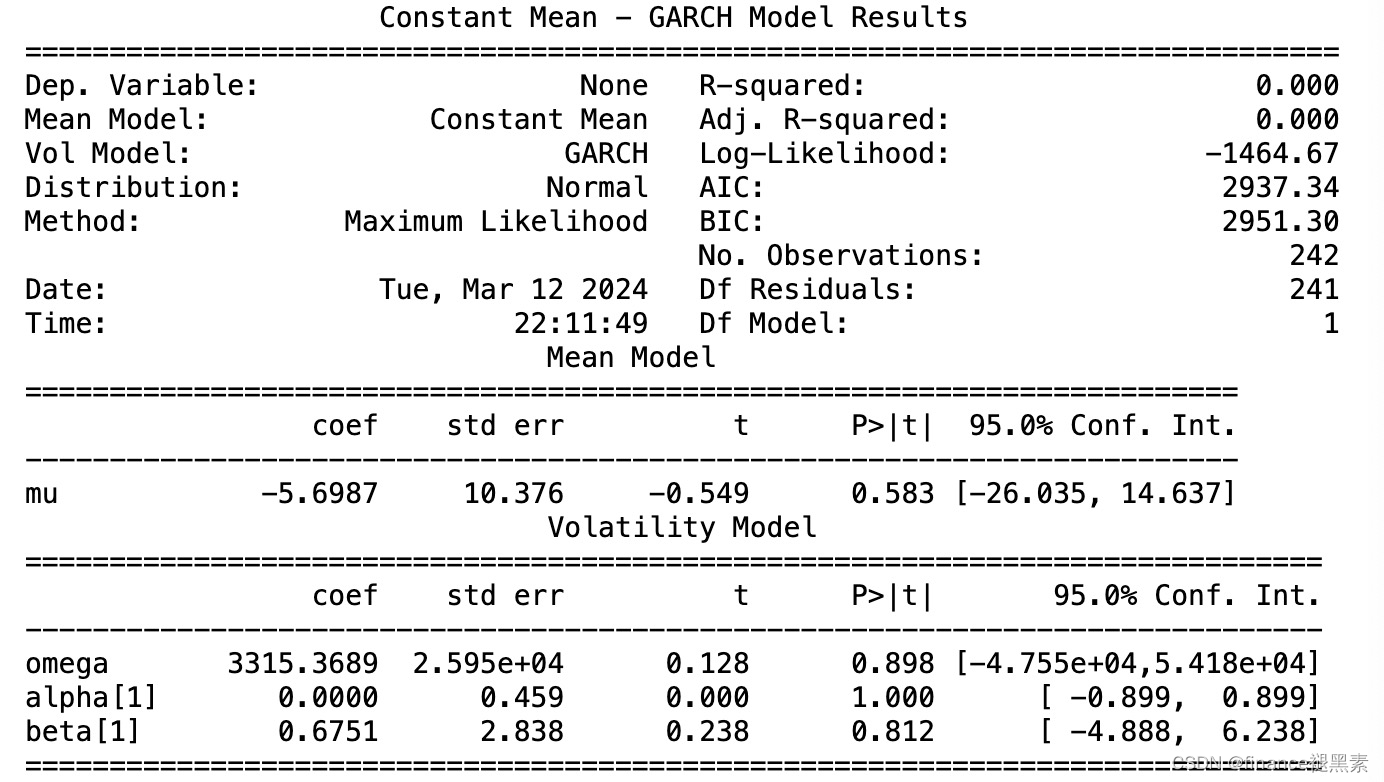
注意上面建立的过程没有参数选取,直接建立的ARMA(1,1)-GARCH(1,1)模型,具体步骤可以根据自己需要添加,模型参数可以在上面修改
根据模型得到的参数结果:
Mean Model (均值模型) Coefficients:
mu (常数项): -5.6987 (常数项的系数)
std err (标准误差): 10.376 (系数的标准误差)
t (t统计量): -0.549 (t统计量,用于检验系数是否显著)
P>|t| (P值): 0.583 (P值,用于判断系数是否显著)
Conf. Int. (置信区间): [-26.035, 14.637] (95%的置信区间)
Volatility Model (波动性模型) Coefficients:
omega (常数项): 3315.3689 (GARCH模型的常数项)
std err (标准误差): 2.595e+04 (系数的标准误差)
t (t统计量): 0.128 (t统计量,用于检验系数是否显著)
P>|t| (P值): 0.898 (P值,用于判断系数是否显著)
Conf. Int. (置信区间): [-4.755e+04, 5.418e+04] (95%的置信区间)
alpha[1] (ARCH项系数): 0.0000 (ARCH项的系数)
beta[1] (GARCH项系数): 0.6751 (GARCH项的系数)
2.3 引入节假日效应和日历效应的虚拟变量的模型建立和结果分析
# 如果要引入二月效应的影响
before_date = '2023-03-01'
df['月份效应'] = 0 # 默认全部为0
df.loc[df['日期'] < pd.to_datetime(before_date), '月份效应'] = 1
建立ARMA模型:
arma_model = ARIMA(df['收盘'], order=(1, 0, 1), exog=df[['新列', '月份效应']])
arma_result = arma_model.fit()
print(arma_result.summary())
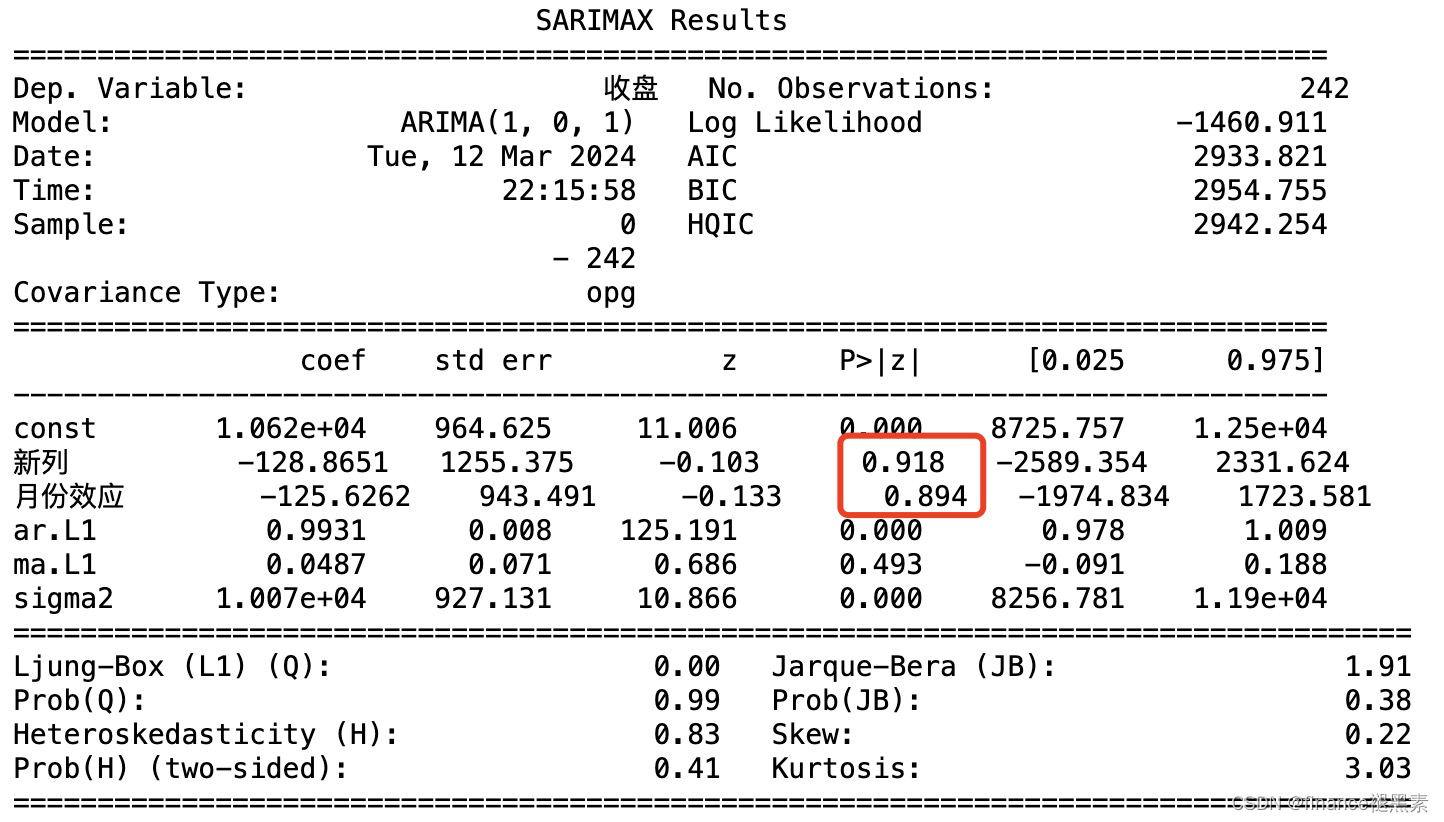
根据P值,节假日效应和日历效应都不显著。(可能是日期选取在一年内太少造成的)
进一步建立ARMA-GARCH模型:
garch_model = arch_model(arma_result.resid, vol='Garch', p=1, q=1)
garch_result = garch_model.fit()
print(garch_result.summary())
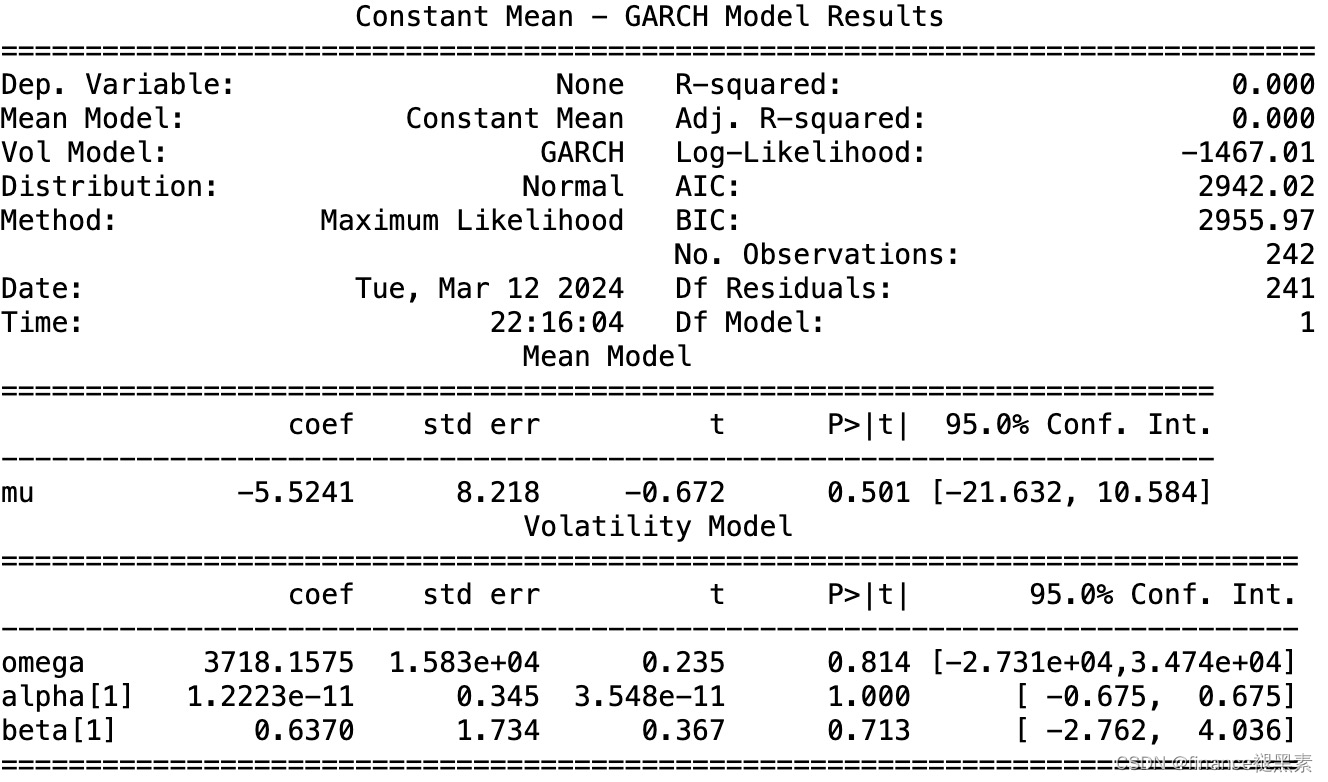
3. 结语
其他文章有进一步预测未来波动率的,也有关于结果检验、误差检验的相关文章。不当之处敬请斧正。
原文代码可关注gzh‘finance褪黑素’,在gzh下回复关键字【20240312】获取。