2471. 逐层排序二叉树所需的最少操作数目

目录

1、循环标记置换环

2、并查集置换环 

---

思路：

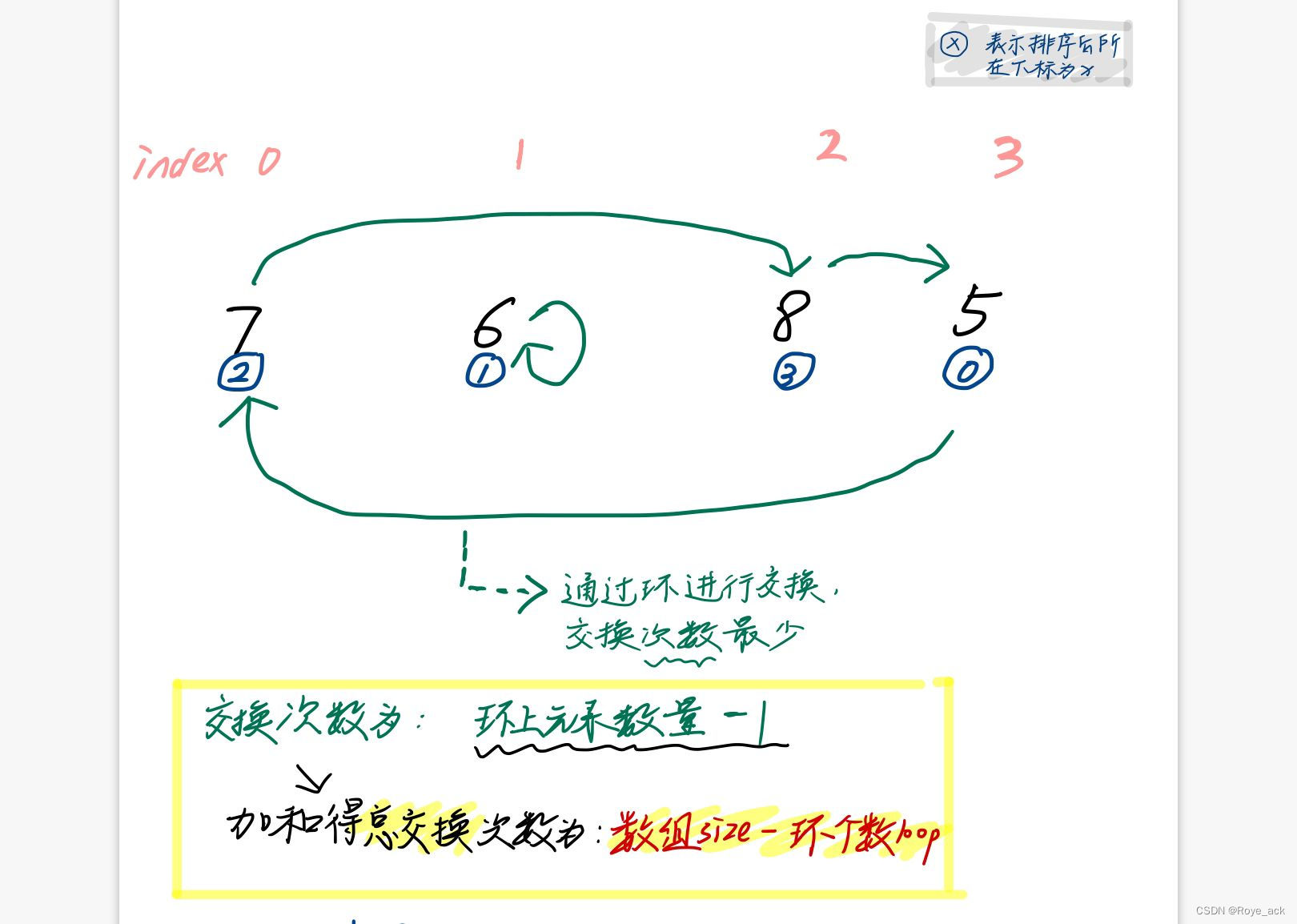
总操作数目 = 每一层最小操作数之和 = 每一层元素个数 - 置换环数

先用bfs对树进行层序遍历，一层一层地计算

置换环：对每个节点，将其指向它应该放到的正确位置，直到首尾相接形成了一个环

则最小交换次数 = 环中元素个数-1

则 每一层的总交换次数 = 每一层元素个数 - 置换环数

如何找出置换环？

• 用map记录每一个节点的正确位置，比如【7，6，8，5】
• mp[7]=2   mp[6]=1  mp[8]=3  mp[5]=0
• st数组负责标记入环的节点，从第一个节点7入手
• 将坐标为0的7标记，并将7指向正确的位置，也就是mp[7]=2
• 将坐标为2的8标记，并将8指向正确的位置，也就是mp[8]=3
• 将坐标为3的5标记，并将5指向正确的位置，也就是mp[5]=0
• 此时0之前已经被标记过，则说明这是一个置换环，上述过程用cnt统计置换环元素个数

所以每一层的最小操作数pre+=cnt-1

1、循环标记置换环

class Solution {
public:
    int minimumOperations(TreeNode* root) {
        int res=0;
        if(root==nullptr) return res;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            vector<int> v;
            int n=q.size();

            //存入每一层的结点
            for(int i=0;i<n;i++)
            {
                TreeNode* x=q.front();
                q.pop();
                v.push_back(x->val);
                if(x->left!=nullptr) q.push(x->left);
                if(x->right!=nullptr) q.push(x->right);
            }
            int per=0,cnt; //per记录每一层交换次数 交换次数=环上元素个数-1
            vector<int> sorted(v);
            sort(sorted.begin(),sorted.end());
            unordered_map<int,int> mp;
            for(int i=0;i<n;i++) mp[sorted[i]]=i;

            vector<bool> st(n,false);
           for(int i=0;i<n;i++) 
            {
                if(!st[i]) //如果v[i]没有入环
                {
                    int j=i;
                    cnt=0;//cnt记录环中元素个数
                    while(!st[j]) //把环内所以元素都标记
                    {
                        int ck=mp[v[j]]; //找到当前节点正确的位置
                        st[j]=true;
                        cnt++;
                        j=ck; //当前节点移到正确的位置
                    }
                    per+=cnt-1;
                }
            }
            res+=per;
        }
        return res;
    }
};

2、并查集置换环 

把在一个置换环里的元素放到一个集合中

有多少个集合就有多少个环 

class Solution {
public:
    vector<int>f;
    int find(int x)
    {
        if(x!=f[x]) f[x]=find(f[x]);
        return f[x];
    }

    void unite(int a,int b)
    {
        int x=find(a),y=find(b);
        if(x!=y) f[x]=y;
    }

    int minimumOperations(TreeNode* root) {
        int res=0;
        if(root==nullptr) return res;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            vector<int> v;
            int n=q.size();

            //存入每一层的结点
            for(int i=0;i<n;i++)
            {
                TreeNode* x=q.front();
                q.pop();
                v.push_back(x->val);
                if(x->left!=nullptr) q.push(x->left);
                if(x->right!=nullptr) q.push(x->right);
            }
            int loop=0;
            vector<int> sorted(v);
            sort(sorted.begin(),sorted.end());
            unordered_map<int,int> mp;
            for(int i=0;i<n;i++) mp[sorted[i]]=i;

            f.resize(n);
            iota(f.begin(),f.end(),0);
            for(int i=0;i<n;i++)
            {
                int ck=mp[v[i]];
                unite(i,ck); //把能成环的放到一个集合
            }

            for(int i=0;i<n;i++) if(f[i]==i) loop++; //统计环个数 有几个父节点就有几个环

            res+=n-loop;
        }
        return res;
    }
};