左偏树，可并堆详解，OJ练习，代码详解

news2024/11/17 0:31:07

文章目录

    • 一、左偏树的定义和性质
      • 1.1优先队列的定义
      • 1.2可并堆的定义
      • 1.3左偏树
        • 1.3.1左偏树的定义
        • 1.3.2左偏树的性质
        • 1.3.3左偏树的合并操作
          • 1.3.3.1合并操作流程
          • 1.3.3.2合并操作的代码实现
      • 1.4左偏树OJ练习
      • 1.4.1模板
        • 1.4.1.1原题链接
        • 1.4.1.2思路分析
        • 1.4.1.3AC代码
      • 1.4.2P1552 [APIO2012] 派遣
        • 1.4.2.1原题链接
        • 1.4.2.2思路分析
        • 1.4.2.3AC代码
      • 1.4.3P4331 [BalticOI 2004] Sequence 数字序列
        • 1.4.3.1原题链接
        • 1.4.3.2思路分析
        • 1.4.3.3AC代码
      • 1.4.4K-Monotonic
        • 1.4.4.1原题链接
        • 1.4.4.2思路分析
        • 1.4.4.3AC代码

一、左偏树的定义和性质

1.1优先队列的定义

优先队列（Priority Queue）是一种抽象的数据类型，它是一种容器，里面存有一些元素，也称为队列中的节点。优先队列的节点要保持一种有序性，这也就要求任意两节点之间可以比较大小。优先队列有三个基本操作：插入节点、取得最小节点、删除最小节点。

1.2可并堆的定义

**可并堆（Mergerable Heap）**也是一种抽象数据类型，它除了支持优先队列的三个基本操作外，还支持一个额外操作——合并操作。

如果不需要合并操作，二叉堆就是我们常用的一种理想的优先队列，但是合并两个二叉堆需要O(n)的时间复杂度，如果直接使用二叉堆朴素合并来作为可并堆的实现，那么合并的时间开销很多时候是我们不能够承受的。

1.3左偏树

1.3.1左偏树的定义

左偏树（Leftlist Tree）是一种具有左偏性质的堆有序的二叉树，是可并堆的一种实现，以下讨论皆为小根堆可并堆。

左偏树的每一个节点x存储的信息包括左右子节点lc[x]，rc[x]，权值v[x]和距离dist[x]。

左儿子或右儿子为空的节点我们称之为外节点。

我们定义节点的距离：节点到达最近的外节点经过的边数。

规定，外界点的距离的-1，空节点的距离为-1

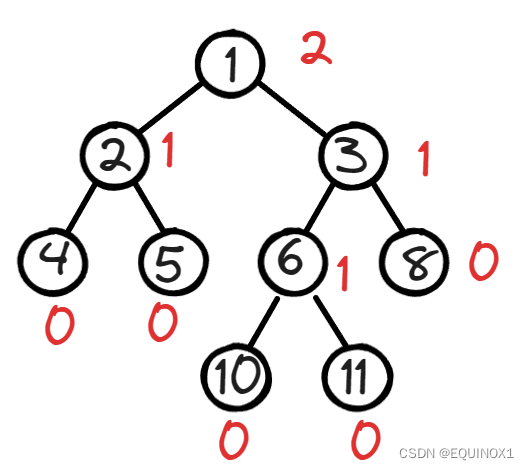
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

1.3.2左偏树的性质
  • 性质1：堆的性质，对于任意节点v[x] <= v[lc[x]]，v[x] <= v[rc[x]]（小根堆）
  • 性质2：左偏性质，左儿子距离 >= 右儿子距离，dist[lc] >= dist[rc]
  • 性质3：任意节点的距离 = 右儿子距离 + 1，dist[x] = dist[rc] + 1
  • 性质4：一棵有n个节点的二叉树，根的dist <= log(n + 1) - 1
    • 证明：
    • 根的距离为x，说明有x + 1层是满二叉树，那么至少有2 ^ (x + 1) - 1个节点，即n >= 2 ^ (x + 1) - 1，则可推出x <= log(n + 1) - 1
1.3.3左偏树的合并操作
1.3.3.1合并操作流程

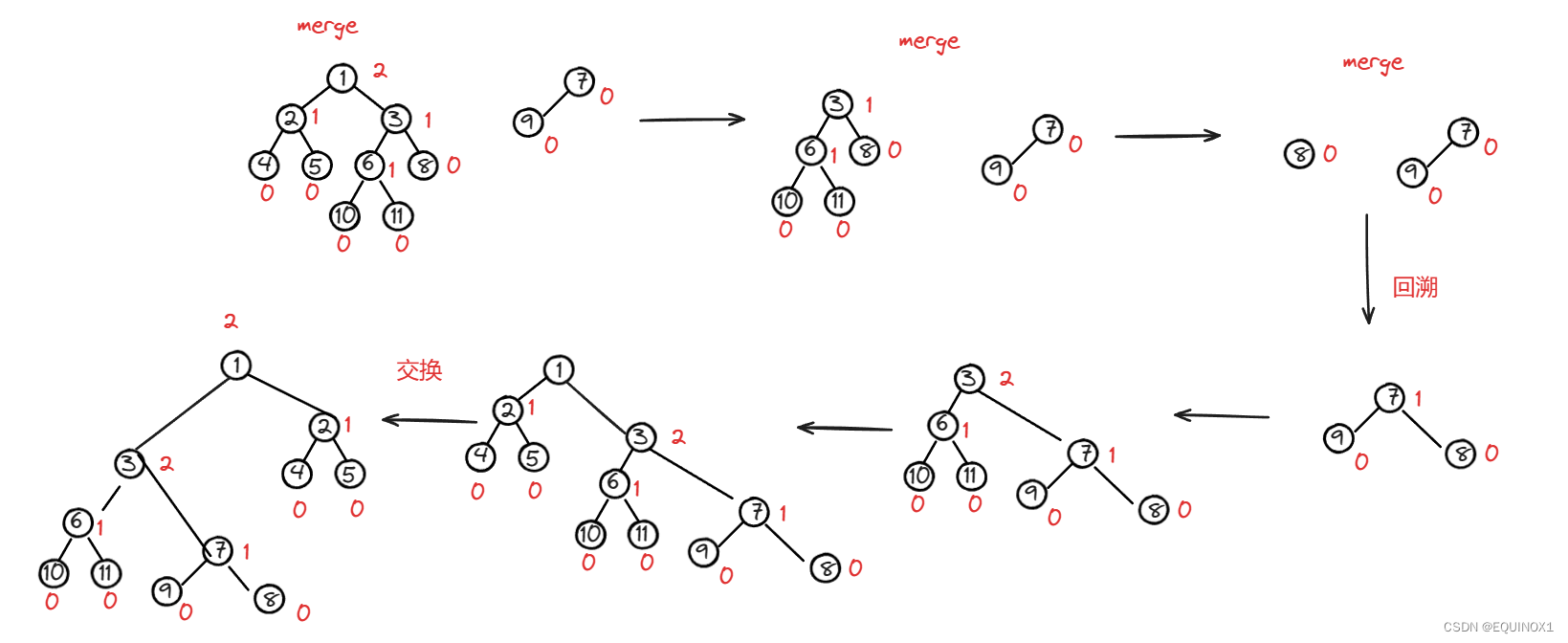
合并操作是左偏树最重要的操作：

  • 维护堆的性质：先取值较小的根作为合并后的根节点，然后递归合并其右儿子和另一个堆，作为合并后的堆的右儿子。
  • 维护左偏性质，合并后如果左儿子的dist小于右儿子的dist，就交换两个儿子
  • 维护根的dist：根的dist为右儿子dist + 1

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

1.3.3.2合并操作的代码实现
//int a[N], p[N], dist[N], lc[N], rc[N], n, m;
int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    if (a[x] == a[y] ? x > y : a[x] > a[y])
        swap(x, y);
    rc[x] = merge(rc[x], y);
    if (dist[lc[x]] < dist[rc[x]])
        swap(lc[x], rc[x]);
    dist[x] = dist[rc[x]] + 1;
    return x;
}

1.4左偏树OJ练习

1.4.1模板

1.4.1.1原题链接

P3377 【模板】左偏树/可并堆 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

1.4.1.2思路分析

题目要求我们实现两种操作，合并两个数所在堆和删除某个数所在堆的最小数

那么我们可以实现一个最小堆的左偏树

但是有个问题，我们还要能够快速找到任意数字所在堆，这我们不难想到在维护可并堆的同时维护一个并查集

实际上我们维护了两棵树，左偏树和并查集树，对于删除的元素我们将其权值置为-1

对操作1：

如果x，y中有某个数字权值为-1，我们跳过

否则找到其所在堆的根px、py，如果px和py不同，就合并px，py，然后更新p[px] = p[py] = merge(px, py)，即合并堆的同时维护并查集

对操作2：

如果x已经删除，那么输出-1，直接跳过

找到堆顶px，然后p[px] = p[lc[px]] = p[rc[px]] = merge(lc[px], rc[px])

1.4.1.3AC代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N], p[N], dist[N], lc[N], rc[N], n, m;
int findp(int x) { return p[x] == x ? x : p[x] = findp(p[x]); }
int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    if (a[x] == a[y] ? x > y : a[x] > a[y])
        swap(x, y);
    rc[x] = merge(rc[x], y);
    if (dist[lc[x]] < dist[rc[x]])
        swap(lc[x], rc[x]);
    dist[x] = dist[rc[x]] + 1;
    return x;
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    //freopen("in.txt", "r", stdin);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i], p[i] = i;
    dist[0] = -1;
    for (int i = 0, op, x, y; i < m; i++)
    {
        cin >> op;
        if (op == 1)
        {
            cin >> x >> y;
            if (a[x] == -1 || a[y] == -1)
                continue;
            x = findp(x), y = findp(y);
            if (x != y)
                p[x] = p[y] = merge(x, y);
        }
        else
        {
            cin >> x;
            if (a[x] == -1)
            {
                cout << -1 << '\n';
                continue;
            }
            x = findp(x);
            cout << a[x] << '\n';
            a[x] = -1;
            p[lc[x]] = p[rc[x]] = p[x] = merge(lc[x], rc[x]);
        }
    }
    return 0;
}

1.4.2P1552 [APIO2012] 派遣

1.4.2.1原题链接

[P1552 APIO2012] 派遣 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

1.4.2.2思路分析

有点像力扣某道打家劫舍的意思，会想到树形dp

但是树形dp的话我们可以计算某个节点为根的树的最大满意度，但是当预算超出的时候我们就没法调整了

我们考虑自底向上进行遍历，计算每个忍者作为管理者时，其所在子树能够派遣的最大忍者数目以及所花费的钱，然后向前枚举的时候把后面的状态合并进来就行了

这样我们就想到了左偏树

因为左偏树既能让我们在超出预算的时候弹出堆中最大薪水的忍者又能把当前这个堆合并给下一个忍者

1.4.2.3AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
#define int long long
int n, m, ans;
int fa[N], sz[N], sum[N], cost[N], lead[N], root[N], lc[N], rc[N], dist[N];
int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    if (cost[x] < cost[y])
        swap(x, y);
    rc[x] = merge(rc[x], y);
    if (dist[lc[x]] < dist[rc[x]])
        swap(lc[x], rc[x]);
    dist[x] = dist[rc[x]] + 1;
    return x;
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    //freopen("in.txt", "r", stdin);
    cin >> n >> m, dist[0] = -1;
    for (int i = 1; i <= n; i++)
        cin >> fa[i] >> cost[i] >> lead[i], sz[i] = 1, sum[i] = cost[i], root[i] = i, ans = max(ans, lead[i]);
    for (int i = n, f; i >= 1; i--)
    {
        f = fa[i];
        sum[f] += sum[i], sz[f] += sz[i], root[f] = merge(root[f], root[i]);
        while (sum[f] > m)
            sz[f]--, sum[f] -= cost[root[f]], root[f] = merge(lc[root[f]], rc[root[f]]);
        ans = max(ans, sz[f] * lead[f]);
    }
    cout << ans;
    return 0;
}

1.4.3P4331 [BalticOI 2004] Sequence 数字序列

1.4.3.1原题链接

[P4331 BalticOI 2004] Sequence 数字序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

1.4.3.2思路分析

很难想的一道题，但是这道题可以作为求将某序列转化为严格单调序列的最小代价的模板

我们将a[] 和 b[] 都减去下标i得到a’ 和 b’，我们发现Σ|a[i] - b[i]| = Σ|a’[i] - b’[i] - i + i|

显然转化后，绝对值差的和是和原问题等价的

为什么要这样转换呢？

b’i+1 - b’i = bi+1 - bi + i + 1 - i = bi+1 - bi - 1 >= 0，也就是说b‘是一个非降序序列

对于序列a’，它一定是由非降序区间和降序区间组成的

对于非降序区间，我们取b’[i] = a’[i]，显然最优

对于降序区间，我们如果取b’[i] = a’[i]可能无法保证b’非降序，这个时候就要求我们对前面的策略进行调整

有一个广为人知的结论：当x为序列a的中位数时，有Σ|a[i] - x|最小

那么我们此时可以把b’[i]和前面区间合并，直到区间中位数不小于前面区间的中位数，这样就保证了当前处理过的每一段都在最优解

具体步骤：

  • 可并堆的节点为一个区间，保存区间的右端点（左端点可以和前一个区间做差得到），区间中位数下标，区间小于等于中位数的元素个数sz
  • 为了方便和前面的区间合并，我们开一个栈s
  • 将a转化为a’，遍历a‘
    • 开一个右端点为i，小于等于中位数的元素个数为1，中位数下标为i的区间，区间先入栈
    • 如果栈内区间个数大于1，并且栈顶下面那个区间中位数大于栈顶区间中位数，合并两个区间
    • 如果合并后sz > 区间长度/2 + 1，说明堆顶不是中位数因为合并后多了个元素，我们弹出堆顶，保证堆顶就是中位数
    • 如此重复下去直到遍历完a’
  • 遍历栈中区间，每个区间内的b值都是区间中位数加i

这道题比较难想，主要得理解合并后保证每个区间都在最优解

1.4.3.3AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
struct line
{
    int mid, r, sz;
} s[N];
int n, a[N], b[N], lc[N], rc[N], dist[N], top;
int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    if (a[x] < a[y])
        swap(x, y);
    rc[x] = merge(rc[x], y);
    if (dist[lc[x]] < dist[rc[x]])
        swap(lc[x], rc[x]);
    dist[x] = dist[rc[x]] + 1;
    return x;
}
int main()
{
    //freopen("in.txt", "r", stdin);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n, dist[0] = -1;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i], a[i] -= i;
        s[++top] = (line){i, i, 1};
        while (top > 1 && a[s[top - 1].mid] > a[s[top].mid])
        {
            s[top - 1].mid = merge(s[top - 1].mid, s[top].mid);
            s[top - 1].r = s[top].r, s[top - 1].sz += s[top].sz, top--;
            if (s[top].sz > (s[top].r - s[top - 1].r) / 2 + 1)
                s[top].mid = merge(lc[s[top].mid], rc[s[top].mid]), s[top].sz--;
        }
    }
    for (int i = 1, j = 1; i <= top; i++)
        while (j <= s[i].r)
            b[j++] = a[s[i].mid];
    long long res = 0;
    for (int i = 1; i <= n; i++)
        res += abs(a[i] - b[i]);
    cout << res << '\n';
    for (int i = 1; i <= n; i++)
        cout << b[i] + i << ' ';
    return 0;
}

1.4.4K-Monotonic

1.4.4.1原题链接

3016 – K-Monotonic (poj.org)

1.4.4.2思路分析

1.4.3数字序列和POJ3666 Making the Grade的缝合版

关于POJ3666想了解的可以见：线性dp+中位数，POJ3666 Making the Grade-CSDN博客

就是一个基础的dp题目

我们定义f[i][j]为前i个数字划分为j个严格单调区间的最小代价，cost[i][j]为区间[i, j]变为严格单调区间的最小代价

那么有f[i][j] = min(f[i][j], f[i - len][j - 1] + cost[i - len + 1][i])

方程还是很好理解的，我们枚举第i个数所在区间len，那么f[i][j]就能由前i-len个数字划分为j - 1个严格单调区间以及i - len + 1到i转化为严格单调区间的代价转移

我们方程的总时间复杂度为O(n^2 * k)，k才10，n也就1000，时间复杂度是够的

那么如何求cost呢？我们发现求区间变成严格单调区间的代价就是1.4.3数字序列那道题目

所以我们只需要按照1.4.3数字序列的方法预处理cost即可，注意到题目要求的是单调区间，所以我们要递增求一次，递减求一次

1.4.3数字序列中我们相当于在O(nlogn)内求出了cost[1][n]，实际上我们已经计算了cost[i][n]，只需要枚举的时候维护一下即可

这要求我们能够快速求出区间内Σ|ai - mid|

设区间内一共由tot_sz个数字，小于等于中位数的有tr_sz个数字，区间总和为tot_sum，小于等于中位数的总和为tr_sum

那么区间内的贡献就是mid * tr_sz - tr_sum + tot_sum - tr_sum - (tot_sz - tr_sz) * mid

这四个值在合并的时候也都很好维护，详细看代码即可

1.4.4.3AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1010;
int a[N], lc[N], rc[N], dist[N], cost[N][N], f[N][12], top, n, k;
struct line
{
    int mid, r, tot_sum, tot_sz, tr_sum, tr_sz;
    int get_cost()
    {
        return a[mid] * tr_sz - tr_sum + tot_sum - tr_sum - (tot_sz - tr_sz) * a[mid];
    }
} s[N];
int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    if (a[x] < a[y])
        swap(x, y);
    rc[x] = merge(rc[x], y);
    if (dist[lc[x]] < dist[rc[x]])
        swap(lc[x], rc[x]);
    dist[x] = dist[rc[x]] + 1;
    return x;
}
void cal(int idx)
{
    top = 0, memset(s, 0, sizeof s), memset(lc, 0, sizeof lc), memset(rc, 0, sizeof rc), memset(dist, 0, sizeof dist), dist[0] = -1, s[0].r = idx - 1;
    for (int i = idx, res = 0; i <= n; i++)
    {
        s[++top].mid = i, s[top].r = i, s[top].tot_sum = s[top].tr_sum = a[i], s[top].tot_sz = s[top].tr_sz = 1;
        while (top > 1 && a[s[top - 1].mid] > a[s[top].mid])
        {
            res -= s[top - 1].get_cost();
            s[top - 1].mid = merge(s[top - 1].mid, s[top].mid);
            s[top - 1].r = s[top].r, s[top - 1].tot_sum += s[top].tot_sum, s[top - 1].tr_sum += s[top].tr_sum, s[top - 1].tr_sz += s[top].tr_sz, s[top - 1].tot_sz += s[top].tot_sz, top--;
            while (s[top].tr_sz > (s[top].r - s[top - 1].r) / 2 + 1)
                s[top].tr_sum -= a[s[top].mid], s[top].tr_sz--, s[top].mid = merge(lc[s[top].mid], rc[s[top].mid]);
        }
        res += s[top].get_cost();
        cost[idx][i] = min(cost[idx][i], res);
    }
}
signed main()
{
    //freopen("in.txt", "r", stdin);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    while (cin >> n >> k, n)
    {
        memset(cost, 0x3f, sizeof cost);
        for (int i = 1; i <= n; i++)
            cin >> a[i], a[i] -= i;
        for (int i = 1; i <= n; i++)
            cal(i);
        for (int i = 1; i <= n; i++)
            a[i] += i, a[i] = -a[i], a[i] -= i;
        for (int i = 1; i <= n; i++)
            cal(i);
        memset(f, 0x3f, sizeof f), f[0][0] = 0;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= k; j++)
                for (int len = 1; len <= i; len++)
                    f[i][j] = min(f[i][j], f[i - len][j - 1] + cost[i - len + 1][i]);
        cout << f[n][k] << '\n';
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1506609.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++的类与对象（五）：赋值运算符重载与日期类的实现

C++的类与对象（五）：赋值运算符重载与日期类的实现

目录 比较两个日期对象 运算符重载 赋值运算符重载 连续赋值 日期类的实现 Date.h文件 Date.cpp文件 Test.cpp文件 const成员 取地址及const取地址操作符重载 比较两个日期对象 问题描述&#xff1a;内置类型可直接用运算符比较&#xff0c;自定义类型的对象是多个…
阅读更多...
【Leetcode每日一刷】滑动窗口：209.长度最小的子数组

【Leetcode每日一刷】滑动窗口：209.长度最小的子数组

一、209.长度最小的子数组 1.1&#xff1a;题目 题目链接 1.2&#xff1a;解题思路 题型&#xff1a;滑动窗口&#xff1b;时间复杂度&#xff1a;O(n) &#x1faa7; 滑动窗口本质也是双指针的一种技巧&#xff0c;特别适用于字串问题 ❗❗核心思想/ 关键&#xff1a;左右…
阅读更多...
简洁的链式思维（CCoT）提示

简洁的链式思维（CCoT）提示

原文地址&#xff1a;Concise Chain-of-Thought (CCoT) Prompting 传统的CoT导致了输出令牌使用的增加&#xff0c;而CCoT提示是一种旨在减少LLM响应的冗长性和推理时间的提示工程技术。 2024 年 1 月 24 日 Areas where Chain-Of-Thought-like methodology has been introd…
阅读更多...
RabbitMQ - 07 - 通过注解创建队列和交换机

RabbitMQ - 07 - 通过注解创建队列和交换机

之前消息模型的实现,都是通过rabbitMQ Management 控制台来手动创建 queue 和 exchange 的 在项目开发中有两种方式通过代码声明 创建 一种是通过 Bean 方式,这种代码量较大 稍繁琐 一种是通过注解的方式声明 先编写消费者代码 通过注解绑定了 消息队列,交换机,还有 routin…
阅读更多...
24 深度卷积神经网络 AlexNet【李沐动手学深度学习v2课程笔记】（备注：含AlexNet和LeNet对比）

24 深度卷积神经网络 AlexNet【李沐动手学深度学习v2课程笔记】（备注：含AlexNet和LeNet对比）

目录 1. 深度学习机器学习的发展 1.1 核方法 1.2 几何学 1.3 特征工程 opencv 1.4 Hardware 2. AlexNet 3. 代码 1. 深度学习机器学习的发展 1.1 核方法 2001 Learning with Kernels 核方法 &#xff08;机器学习&#xff09; 特征提取、选择核函数来计算相似性、凸优…
阅读更多...
Python爬虫打印状态码为521，返回数据为乱码？

Python爬虫打印状态码为521，返回数据为乱码？

爬虫代码&#xff1a; import requests headers {User-Agent:Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/107.0.0.0 Safari/537.36,Referer:https://www1.rmfysszc.gov.cn/projects.shtml?dh3&gpstate1&wsbm_slt1} …
阅读更多...
Java 中的 File 类常用方法介绍

Java 中的 File 类常用方法介绍

Java 中的 File 类是 java.io 包的一部分&#xff0c;它提供了丰富的文件操作方法。File 类可以用来表示文件和目录路径名的抽象表示形式&#xff0c;即它可以用来获取文件或目录的属性&#xff0c;也可以用来创建、删除、重命名文件和目录。下面是一些常用的 File 类方法&…
阅读更多...
双体系Java学习之程序流程控制及选择结构

双体系Java学习之程序流程控制及选择结构

程序流程控制 选择结构 package struct;import java.util.Scanner;public class IfDemo01 {public static void main(String[] args) {Scanner scanner new Scanner(System.in);System.out.println("请输入内容&#xff1a;");String s scanner.nextLine();//判断字…
阅读更多...
elasticsearch篇

elasticsearch篇

1.初识elasticsearch 1.1.了解ES 1.1.1.elasticsearch的作用 elasticsearch是一款非常强大的开源搜索引擎&#xff0c;具备非常多强大功能&#xff0c;可以帮助我们从海量数据中快速找到需要的内容 例如&#xff1a; 在电商网站搜索商品 在百度搜索答案 在打车软件搜索附近…
阅读更多...
鸿蒙Harmony应用开发—ArkTS声明式开发（通用属性：动态属性设置）

鸿蒙Harmony应用开发—ArkTS声明式开发（通用属性：动态属性设置）

动态设置组件的属性&#xff0c;支持开发者在属性设置时使用if/else语法&#xff0c;且根据需要使用多态样式设置属性。 说明&#xff1a; 从API Version 11开始支持。后续版本如有新增内容&#xff0c;则采用上角标单独标记该内容的起始版本。 attributeModifier attributeMo…
阅读更多...
AI Vtuber一款聚合了多种大模型技术的虚拟主播

AI Vtuber一款聚合了多种大模型技术的虚拟主播

大家好&#xff0c;笔者荒生&#xff0c;今天调研了一款比较不错的开源项目AI-Vtuber&#xff0c;和大家一起分享。 AI-Vtuber是一款数字人虚拟直播软件&#xff0c;聚合了多种多种市面主流大模型技术&#xff0c;可谓牛得一逼。包括&#xff1a;支持ChatGPT、Claude、ChatGLM…
阅读更多...
C语言学习--练习4(二维数组)

C语言学习--练习4(二维数组)

目录 1.统计有序数组中的负数 2.矩阵对角线元素和 3.最富有客户的资产总量 4.托普利兹矩阵 5.矩阵中的幸运数 6.二进制矩阵中的特殊位置 7.岛屿的周长 1.统计有序数组中的负数 //直接遍历二维数组即可 int countNegatives(int** grid, int gridSize, int* gridColSize) …
阅读更多...
20240310-2-数组（Array）

20240310-2-数组（Array）

数组&#xff08;Array&#xff09; 面试中最常见的就是围绕数组进行出题&#xff0c;主要原则数组可以随机读取&#xff0c;一般遇到数组相关的题目&#xff0c;都不是直观看到的那样。第一步暴力解法&#xff0c;第二步是否可以排序&#xff0c;是否可以二分&#xff0c;是否…
阅读更多...
【Linux】线程封装_互斥

【Linux】线程封装_互斥

欢迎来到Cefler的博客&#x1f601; &#x1f54c;博客主页&#xff1a;折纸花满衣 &#x1f3e0;个人专栏&#xff1a;题目解析 &#x1f30e;推荐文章&#xff1a;【LeetCode】winter vacation training 目录 &#x1f449;&#x1f3fb;线程封装Thread.cpp &#x1f449;&am…
阅读更多...
给 spyter/all-spark-notebook 添加scala支持

给 spyter/all-spark-notebook 添加scala支持

spyter/all-spark-notebook默认没有安装scala notebook&#xff0c;需要手动添加。 你可以创建一个新的 Dockerfile&#xff0c;在其中添加你需要的配置和组件。以下是一个简单的例子&#xff1a; FROM jupyter/all-spark-notebook:x86_64-ubuntu-22.04 #冒号后可以是latest&a…
阅读更多...
Masked Generative Distillation（MGD）2022年ECCV

Masked Generative Distillation（MGD）2022年ECCV

Masked Generative Distillation&#xff08;MGD&#xff09;2022年ECCV 摘要 **目前的蒸馏算法通常通过模仿老师的输出来提高学生的表现。本文表明&#xff0c;教师还可以通过引导学生特征恢复来提高学生的代表性。从这个角度来看&#xff0c;我们提出的掩模生成蒸馏&#x…
阅读更多...
扩展学习|系统理解数字经济

扩展学习|系统理解数字经济

文献来源&#xff1a;[1]肖静华,胡杨颂,吴瑶.成长品&#xff1a;数据驱动的企业与用户互动创新案例研究[J].管理世界,2020,36(03):183-205.DOI:10.19744/j.cnki.11-1235/f.2020.0041. [2]陈晓红,李杨扬,宋丽洁等.数字经济理论体系与研究展望[J].管理世界,2022,38(02):208-22413…
阅读更多...
微信小程序跳转到其他小程序

微信小程序跳转到其他小程序

有两种方式&#xff0c;如下&#xff1a; 一、appid跳转 wx.navigateToMiniProgram({appId: 目标小程序appid,path: 目标小程序页面路径,//不配的话默认是首页//develop开发版&#xff1b;trial体验版&#xff1b;release正式版envVersion: release, success(res) {// 打开成功…
阅读更多...
yudao-cloud 学习笔记

yudao-cloud 学习笔记

前端代码 浏览器打开 https://cloud.iocoder.cn/intro/ F12 执行代码 var aaa $(".sidebar-group-items").find("a"); var ll[]; var tt[]; for(var i0;i<aaa.length;i ){ ll.push("https://doc.iocoder.cn" $(aaa[i]).attr("href&quo…
阅读更多...
电动车窗开关中MOS管的应用解析

电动车窗开关中MOS管的应用解析

随着科技的不断发展&#xff0c;电动车窗系统已经成为现代汽车中不可或缺的一部分。而MOS&#xff08;金属氧化物半导体&#xff09;管的应用&#xff0c;为电动车窗开关注入了新的活力&#xff0c;极大地提高了其使用寿命和安全性。 一、MOS的优越性能 MOS管以其卓越的开关…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023