SH33F2811包含三相电机的空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)算法,对应于交流感应电机或永磁同步电机中的三相电压源逆变器的功率器件的一种特殊的开关触发顺序和脉宽大小的组合。这种开关触发顺序和组合将在定子线圈中产生三相互差120°电角度的正弦波电流。
目录
SVPWM算法原理
SVPWM算法实现过程
五段式SVPWM算法
七段式SVPWM算法
Sign算法
饱和算法
内容拓展
SVPWM算法原理
考虑如下图所示的逆变器,
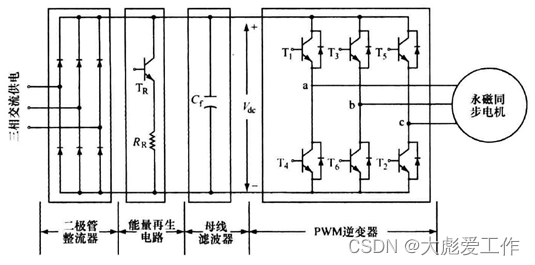
以直流电源的负极作为参考点来研究a相的重点电压Va,该电压由一系列的开关组合Sa,即下表种所包含晶体管T1和T4的开关组合所决定的。
| T1 | T4 | Sa | Va |
| 导通 | 关断 | 1 | Vdc |
| 关断 | 导通 | 0 | 0 |
对应于b相与c相桥臂的开关状态Sb及Sc可以通过类似的方式推导获得。Sa、Sb及Sc总共8种开关状态,下表列举了这8种开关状态以及推导出的线电压、相电压。
| Sa | Sb | Sc | 矢量 | Uab | Ubc | Uca | Uan | Ubn | Ucn |
| 0 | 0 | 0 | U0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | U4 | Udc | 0 | -Udc | 2/3Udc | -1/3Udc | -1/3Udc |
| 1 | 1 | 0 | U6 | 0 | Udc | -Udc | 1/3Udc | 1/3Udc | -2/3Udc |
| 0 | 1 | 0 | U2 | -Udc | Udc | 0 | -1/3Udc | 2/3Udc | -1/3Udc |
| 0 | 1 | 1 | U3 | -Udc | 0 | Udc | -2/3Udc | 1/3Udc | 1/3Udc |
| 0 | 0 | 1 | U1 | 0 | -Udc | Udc | -1/3Udc | -1/3Udc | 2/3Udc |
| 1 | 0 | 1 | U5 | Udc | -Udc | 0 | 1/3Udc | -2/3Udc | 1/3Udc |
| 1 | 1 | 1 | U7 | 0 | 0 | 0 | 0 | 0 | 0 |
根据表中八个基本矢量的情况,画出八个基本电压空间矢量的大小和位置(以a相和α轴方向重合为例),电压空间矢量图如下:
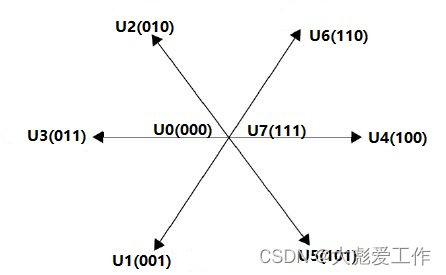
图1 电压空间矢量图
其中6个非零矢量的幅值相同(在两轴静止坐标系下,模长为2Udc/3;在三相静止坐标系下,模长为Udc),相邻的矢量相差60°,两个零矢量幅值为零,位于中心。
在SH33F2811的空间矢量脉宽调制算法中,是以U4(001)为α轴方向,扇区计数从0开始,如下图所示:
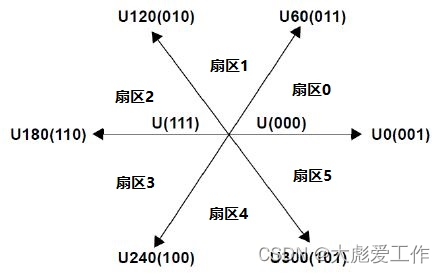
图2 SH33F2811电压空间矢量图
空间矢量调制的过程允许通过两个相邻矢量各分量的和来表示任何空间电压矢量。在下图中,UOUT是期望的空间电压矢量。该矢量位于U60和U0之间的区间内。如果在给定PWM周期T期间,U0的输出时间为T1/T而U60的输出时间为T2/T,则整个周期的平均电压值为UOUT。
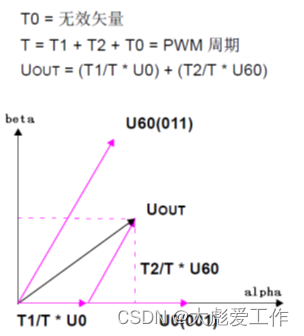
图3 平均空间矢量调制
T0表示绕组上无有效电压的时间;即施加了无效矢量。在六个区间的每个区间中,一个轴与该区间正好相反,而其它两个轴对称形成该区间的边界。沿着这两个边界轴的矢量分量分别为T1和T2。
SVPWM算法实现过程
首先将静止2轴α-β坐标系变换到定义的静止3轴参考坐标系,需要两个静止坐标系的Uα和Uβ输入。如下所示:
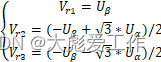
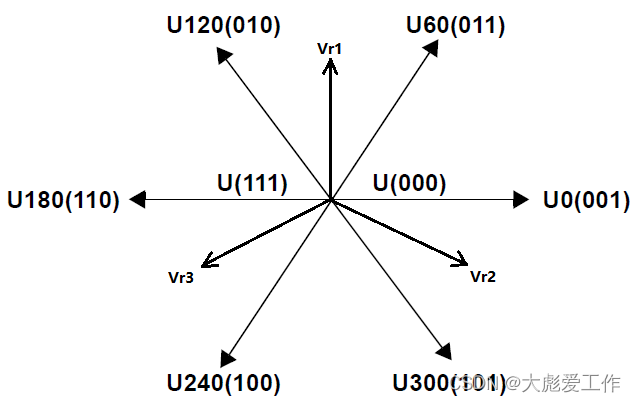
图4 Vr1\ Vr2\ Vr3关系图
同时定义三个变量a,b,c,如果Vr1>0,则a=1,否则a=0;如果Vr2>0,则b=1,否则b=0;如果Vr3>0,则c=1,否则c=0。再定义一个变量sector,sector = a*1+b*2+c*4,根据sector不同,把空间分为6个扇区。
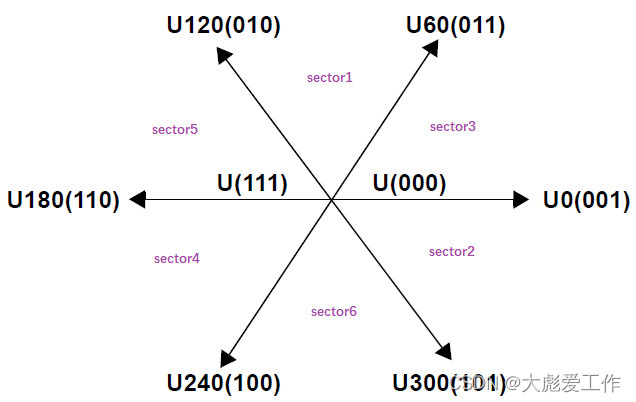
图5 sector定义关系图
另外定义:
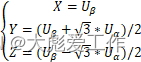
即,X为Vr1方向,Y为Vr3反方向,Z为Vr2反方向。那么,对于不同扇区T1,T2值,有如下对应关系:
| Sector | 1 | 2 | 3 | 4 | 5 | 6 |
| T1 | Z | Y | -Z | -X | X | -Y |
| T2 | Y | -X | X | Z | -Y | -Z |
在PWM周期T中,矢量T1的输出时间为T1/T,而矢量T2的输出时间为T2/T,在剩余时间内输出无效矢量。无效矢量可以由全部为零组成,为五段式SVPWM波形。也可以由中间为全1两边为全零组成,为七段式SVPWM波形。
五段式SVPWM算法
下图为五段式SVPWM波形, PWM信号配置为输出中心对齐,这种配置方法在每个周期内可产生1个线间脉冲。
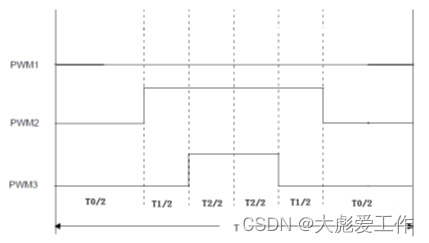
图6 五段式周期T内的PWM
能够实现从Ualpha,Ubeta直接计算出Ta,Tb,Tc三相占空比,输入输出的数据格式可以设定,算法流程图如下:
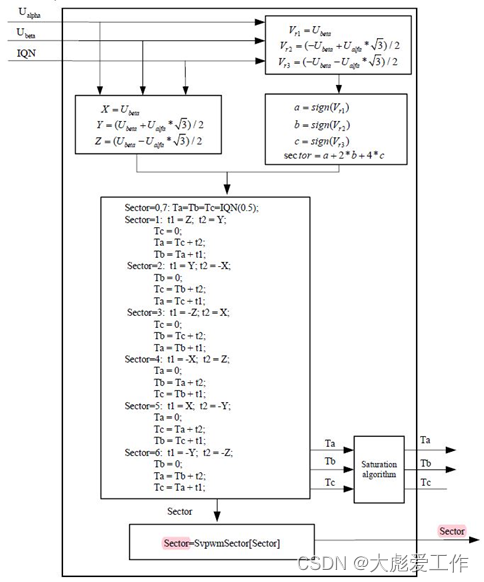
图7 五段式SVPWM算法流程图
注1:Ualpha、Ubeta、T1、T2、Ta、Tb和Tc为有符号32位数,IQN和Sector为无符号8位数。
注2:乘法为IQN格式乘法。
注3:SvpwmSector为一个数组,内容为SvpwmSector[]={0,1,5,0,3,2,4,0}。
注4:图7中标红的Sector对应为图2中的扇区0-5,其他未标红的Sector对应为图5中的Sector1-6.
七段式SVPWM算法
下图为七段式SVPWM波形, PWM信号配置为输出中心对齐,这种配置方法在每个周期内可产生两个线间脉冲,有效开关频率加倍,纹波电流减小,同时并未增加功率器件的开关损耗。
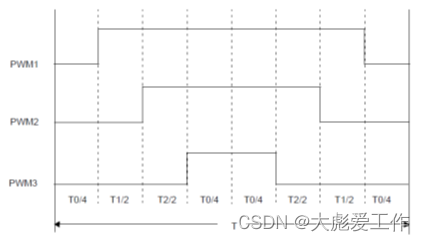
图8 七段式SVPWM算法流程图
能够实现从Ualpha,Ubeta直接计算出Ta,Tb,Tc三相占空比,输入输出的数据格式可以设定,算法流程图如下:
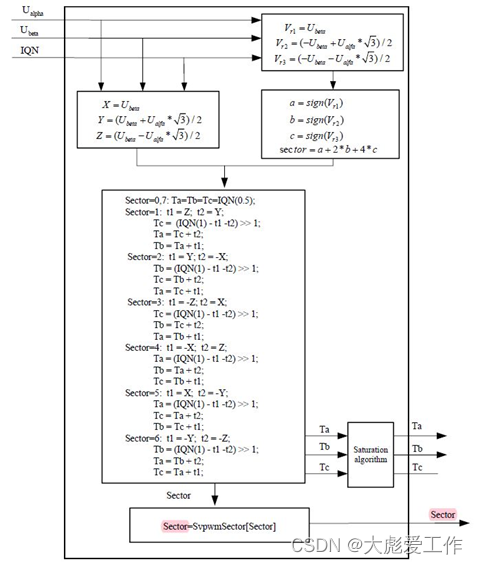
图9 七段式SVPWM算法流程图
注1:Ualpha、Ubeta、T1、T2、Ta、Tb和Tc为有符号32位数,IQN和Sector为无符号8位数。
注2:乘法为IQN格式乘法。
注3:SvpwmSector为一个数组,内容为SvpwmSector[]={0,1,5,0,3,2,4,0}。
注4:图9中标红的Sector对应为图2中的扇区0-5,其他未标红的Sector对应为图5中的Sector1-6.
Sign算法
图7图9中的sign为符号算法,详细的算法如下:
例如a = sign(x):
if (x > 0)
a = 1;
else
a = 0;
饱和算法
不管五段式还是七段式,都可能存在计算溢出情况,当Ta/Tb/Tc任何一个计算结果超出范围,则都会置起溢出标志位OVER@SVIQN。为了防止计算结果溢出,增加了对Ta,Tb和Tc的饱和处理,通过寄存器SATEN@SVIQN来选择是否使能饱和,详细算法如下:
if(Tx < 0)
{
OVER@SVIQN = 1;
if (1 == SATEN@SVIQN)
{
Tx = 0;
}
}
else if(Tx > IQN(1))
{
OVER@SVIQN = 1;
if(1 == SATEN@SVIQN)
{
Tx = IQN(1);
}
}
注1:x=a,b,c
注2:整个SVPWM硬件计算时间为3个AHB CLK。
注3:溢出标志位的值在每次计算时都更新。
内容拓展
《小试牛刀》