论文题目:A Novel Dynamic Multiobjective Optimization Algorithm With Hierarchical Response System
一种新的具有分层响应系统的动态多目标优化算法(Han Li , Zidong Wang , Fellow, IEEE, Chengbo Lan, Peishu Wu , and Nianyin Zeng , Member, IEEE)IEEE TRANSACTIONS ON COMPUTATIONAL SOCIAL SYSTEMS,2024
刚开始学习多目标优化算法,不作商业用途,如果有不正确的地方请指正!
个人总结:
Introduction 写的挺好的.
提出了一个CD参数代表环境变化程度,如果环境变化不低于最小值就简单的从之前的非支配解中进行优化为下一代.
如果环境变化在设置的阈值之间就使用TL模型对PT-1的种群进行知识迁移.
如果环境变化超过了阈值的最大值就保留一定的上一时刻的非支配借,并对种群进行初始化.
引言
目前存在的问题
在动态行为的情况下,如果不对反应做出进一步的分析,就很难找出有用的历史经验;
在一些微小变化的情况下,引入新个体似乎是不必要的,而且当环境中存在剧烈变化时,基于预测的响应可能会导致进化向不合适的方向发展。
本文提出的想法
设计一种能够定量测量环境变化的新型DMOA,以便采取相应的响应策略。
在环境变化较小的情况下,建议采用先前基于PS的精化策略,以节省不必要的计算,并跟踪几乎不变的PF
相反,在发生剧烈变化的情况下,由于在完全不同的环境中搜索Pareto解可以直接视为解决一个新问题,因此采用了一种直观的思想(把个体引入到新的环境中)
除了上述两种极端情况,还应用了TL响应策略来加速收敛,其主要思想是在新的环境中传递有用的历史知识以提供高质量的初始种群。
总体算法:将环境变化量化并分为三个层次。本文提出的算法(命名为HRS - DMOA)实质上是一个两阶段算法:
- 首先选取前一环境中非支配解的一半作为传感器来量化动态行为;并且相应地,基于两个预定义的阈值
- 后期可采用3种响应策略在新环境中生成初始种群,以加速收敛。特别地,在剧烈变化的情况下采用基于多样性的策略,当变化处于中等水平时,考虑TL响应方法的新颖前沿,该方法结合了记忆和预测在解决DMOPs中的流行思想。
背景及相关工作
略过一下
方法论
详细阐述了所提出的HRS-DMOA,其主要思想是通过一些量化程序对环境变化进行分级,以便可以相应地采用分层响应
A.Environmental Change Quantification(环境变化的量化)
之前看了很多的文章,对环境改变的检测基本就是10%的个体检测,比较的无脑.
这篇文章中选择前一环境中的一半非支配解来形成传感器集S,用于估计目标函数的变化程度用CD表示
m是目标函数的数量,fi,j(t)表示传感器j在环境t中的第i个适应度值,u=0.001是避免分母等于0.
然后将环境的整体变化程度定义为:
其中 λ 是放大因子,设置为 m − 1
B.Hierarchical Response System(分层响应系统)
根据环境的变化度CD,使用两个预定义的阈值LT和HT将CD划分为三个级别,并相应地采用细化(如果CD<LT)、TL(如果LT≤CD≤HT)和重新初始化(如果CD>HT)的响应模式.
当 CD 小于下限阈值 LT 时,认为变化可以忽略不计,即新环境(表示为 t)与前一个环境(表示为 t − 1)相似。因此,鼓励 PSt−1 不断改进收敛性并寻找帕累托解,其中采用突变算子来进一步补充多样性。
如果 CD 大于较高阈值 HT,则该变化被认为非常显著,以至于以前的大多数搜索经验不再有用。因此,这种情况被视为新的优化问题并重新开始演化,其中 PSt−1 中只有少数解保留在重新初始化的种群中。
如果CD在两个域值之间,则用基于TL的训练模型响应.
在本文中,(LT, HT) 设置为 (0.03, 0.78)
HBS算法伪代码

C.TL-Based Population Initialization(基于TL的种群初始化)
TL 的本质是应用从源域 D 中学到的知识来帮助解决目标域 Dt 中相关但不相同的任务。
随在具有一些突变的先前环境中的 PS 被选为源域 Ds。此外,为了保证知识在正确的方向上转移,在新环境中筛选另一组转移参考点(TRP)以形成目标域Dt。具体来说,应用本地搜索策略将每个具有质量因子 Q(·) 的个体分配为
其中 P 代表种群,Q(·) 值较大的个体被认为具有更好的质量。然后,基于(7),在新环境中的两个种群之间进行比赛,以获得一组TRP以形成Dt。算法 2 中显示了详细信息,其中应用了模拟二元交叉和多项式突变算子以进一步增强多样性 .

设 T = {X, Y } 表示训练集,其中 X = Ds ∪ Dt 和 Y = {0, 1} 是由新时间 t 的支配关系确定的真值标签(Y = 1 表示非支配个体)。

D.HRS-DMOA的总体框架
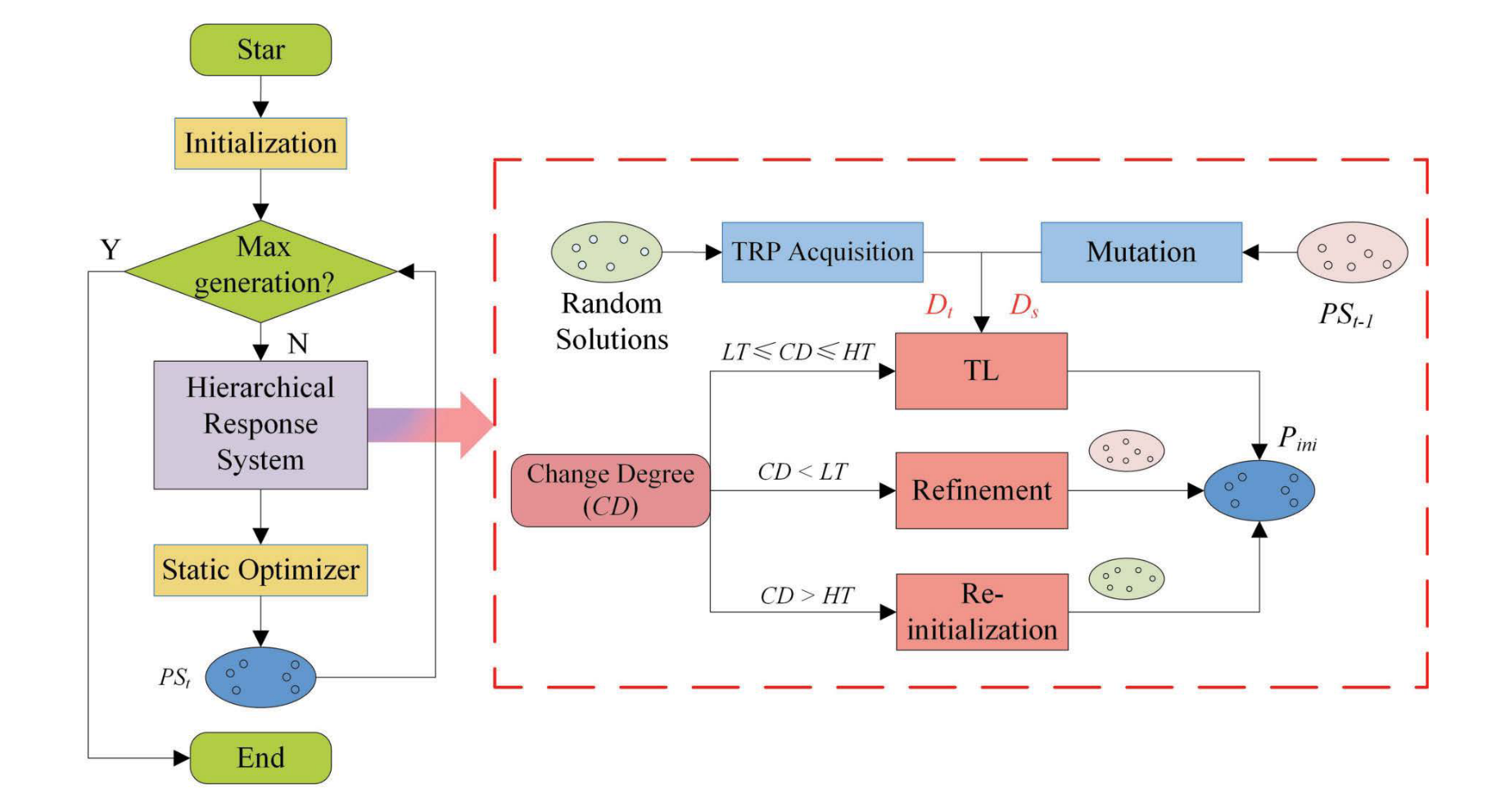
细化:在时间t处,对PSt−1进行多项式突变以增强多样性,并通过从增强的PSt−1中选择获得Pini。
TL:在时间 t 处,应用基于 TL 的初始化来生成 Pini,其中采用增强的 PSt−1 作为源域,并熨平一组 TRP 以形成目标域。
重新初始化:在时间 t 处,PSt−1 中只有少数个体保留在 Pini 中,而 Pini 的其余部分则直接通过随机初始化生成。