A:Turtle Puzzle: Rearrange and Negate

思路:
将负的元素全部排到一起,然后对它们符号取反,然后求所有元素的和,此时就是最大值了。
代码:
#include<iostream>
using namespace std;
void solve()
{
int n;
cin>>n;
long long ans=0;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
ans+=abs(x);
}
cout<<ans<<endl;
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
}B题:Turtle Math: Fast Three Task

思路:
用set统计每一个数取模3的结果,然后计算所有数的和res,分类讨论
- 如果res正好能够被3模除,那么就返回0
- 如果res取模3余1,那么看如果计算数中有取模3余1的数,那么那个数删除掉就可以模除3,所以只需要操作一次,但如果计算数中没有取模3余1的数,那么我们就只能加上进行两次加1操作,操作次数就是2次。
- 如果res取模3余2,那么无论计算数中有无取模3余2的数,我们的操作无非就是一次加1操作或删除操作,操作次数均是1.
代码:
#include<iostream>
#include<set>
using namespace std;
int solve()
{
int n;
cin>>n;
set<int> S;
long long res=0;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
res+=x;
S.insert(x%3);
}
if(res%3==0) return 0;
else if(res%3==1)
{
if(S.count(1)) return 1; //删除余1的数
else return 2; // 只能让它加2次1
}
else if(res%3==2) return 1; // 不管有没有余数为2的数 最后操作次数都是1
}
int main()
{
int t;
cin>>t;
while (t--) cout<<solve()<<endl;
return 0;
}C.题:Turtle Fingers: Count the Values of k

思路:
因为l的最大范围是10的7次方,所以我们可以用两个指针分别遍历l的所有因子,然后将统计k的数量就可以了,记得去重也可以用set统计
代码:
#include<iostream>
#include<set>
using namespace std;
typedef long long LL;
void solve()
{
set<int> S;
int x,y,l;
cin>>x>>y>>l;
for(LL i=1;l%i==0;i*=x)
//因为第二次循环之后i都是先乘x之后在判断的
//所以如果x够大,那么就有可能溢出,所以需要开long long
{
for(LL j=1;l%j==0;j*=y)
{
if(l%(i*j)==0) S.insert(l/i/j);
}
}
cout<<S.size()<<endl;
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
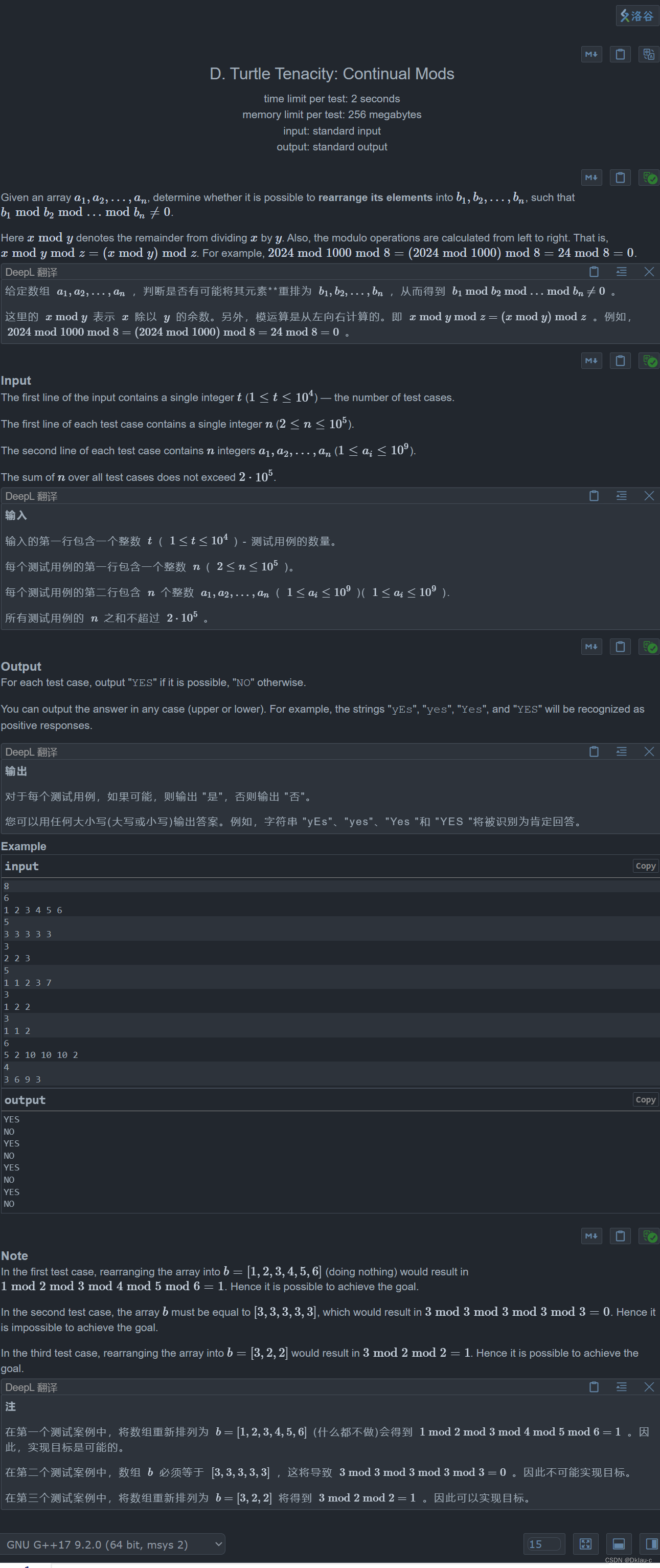
}D:Turtle Tenacity: Continual Mods
思路:
将每个数从小到大排序,判断最小值是否有两个,如果最小值只有一个的话,正常取模下来,结果就是最小值,如果最小值有两个的话,取模下来,结果就是0,所以如果最小值有两个的话,我们就遍历一遍之后的所有数,如果有一个数%最小值之后,不为零,那么就可以把他放到两个最小值之间,取模之后,得到就是更小的最小值,所以最后结果也不为零。如果不存在那么一个数的话,最后结果就只能为0了
代码:
#include<iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int e[N];
void solve()
{
int n;
cin>>n;
for(int i=0;i<n;i++ ) cin>>e[i];
sort(e,e+n);
if(e[0]==e[1])
{
for(int i=2;i<n;i++)
{
if(e[i]%e[0])
{
puts("YES");
return;
}
}
puts("No");
}
else puts("YES");
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
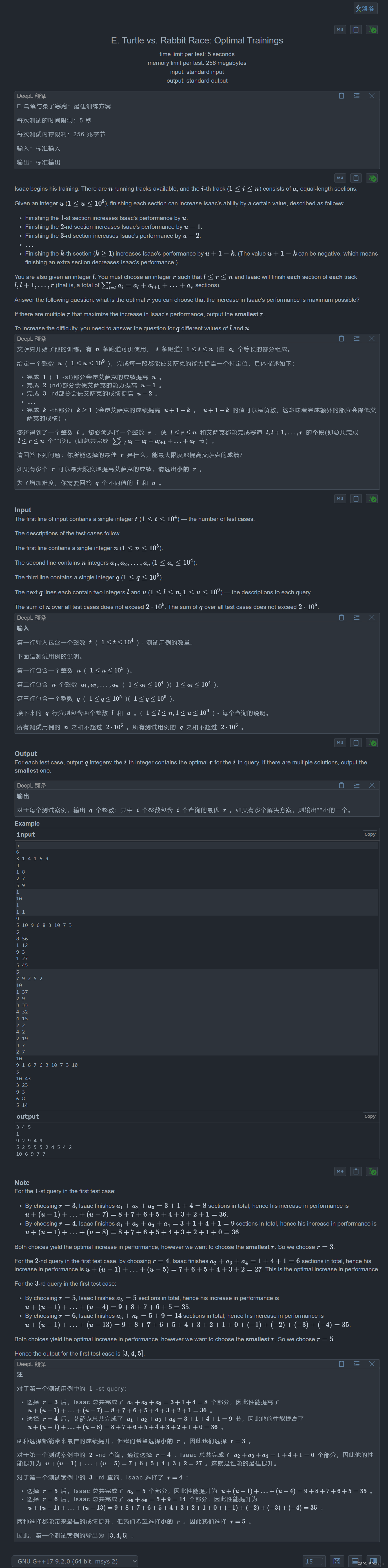
}E:Turtle vs. Rabbit Race: Optimal 训练
思路:
用前缀和计算每一个赛道,锻炼的最优就是让u到0,所以我们可以lower_bound(s[l-1]+u)出来一个r,计算区间和,,需要注意的是,因为lower_bound得出来的是第一个大于等于s[l-1]+u的数,这个数可能并不是最优解,所以我们还需要判断一下二分出来的数-1 所得出的答案注意这个数必须要大于等于l才能成立
代码:
#include<iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;
typedef long long LL;
LL a[N],s[N];
LL calc(int u,LL x)
{
return (2*u-x+1)*x/2;
}
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]=s[i-1]+a[i];
}
int q;
cin>>q;
while (q--)
{
int l,u;
cin>>l>>u;
int j=lower_bound(s+l-1,s+n+1,s[l-1]+u)-s;
LL ans=-1e9;
int r=-1;
if(j<=n)
{
if(calc(u,s[j]-s[l-1])>ans)
{
ans=calc(u,s[j]-s[l-1]);
r=j;
}
}
if(j-1>=l)
{
if(calc(u,s[j-1]-s[l-1])>=ans)
{
ans=calc(u,s[j-1]-s[l-1]);
r=j-1;
}
}
cout<<r<<' ';
}
cout<<endl;
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
}F题:Turtle Mission: Robot and the Earthquake

思路:
BFS模拟,我们不可能考虑每一个石头每次走的位置,这样复杂度太高,所以我们可以根据相对论,机器人向下走一格,也就意味着石头全部都想上走了一格,所以只需要模拟机器人和终点的移动即可,
此时机器人向下走就变成了向下走两格,向右走变成了向右下走一格,向上走变成了静止不动。
因为终点列是没有石头的,所以我们可以计算走到终点列的最短距离,然后计算所在行距离终点的位置,也就是等待终点来的时间。
那么怎么计算走到终点列的最短距离呢,就可以用BFS(向下两格,或向右下一个)然后计算ans=到终点列的距离+((所在行-终点的移动)%n+n)%n
终点的移动:n-1+到终点列的距离(时间)
最后注意无解的情况就可以了
代码:
#include <iostream>
#include <queue>
using namespace std;
const int N=1e3+10;
int d[N][N];
int a[N][N];
void solve()
{
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
cin>>a[i][j];
d[i][j]=-1;
}
queue<pair<int,int>> q;
q.push({0,0});
d[0][0]=0;
int dx[2]={2,1},dy[2]={0,1};
int ans=1e9;
while (!q.empty())
{
auto t=q.front();
q.pop();
if(t.second==m-1)
{
ans=min(ans,d[t.first][t.second]+((t.first-(n-1+d[t.first][t.second]))%n+n)%n);
}
for(int i=0;i<2;i++)
{
int x=(t.first+dx[i])%n,y=(t.second+dy[i]);
if(y<m && d[x][y]==-1 && a[x][y]==0)
{
if(i==0 && a[(t.first+1)%n][y]==1) continue;
d[x][y]=d[t.first][t.second]+1;
q.push({x,y});
}
}
}
if(ans==1e9) puts("-1");
else cout<<ans<<endl;
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
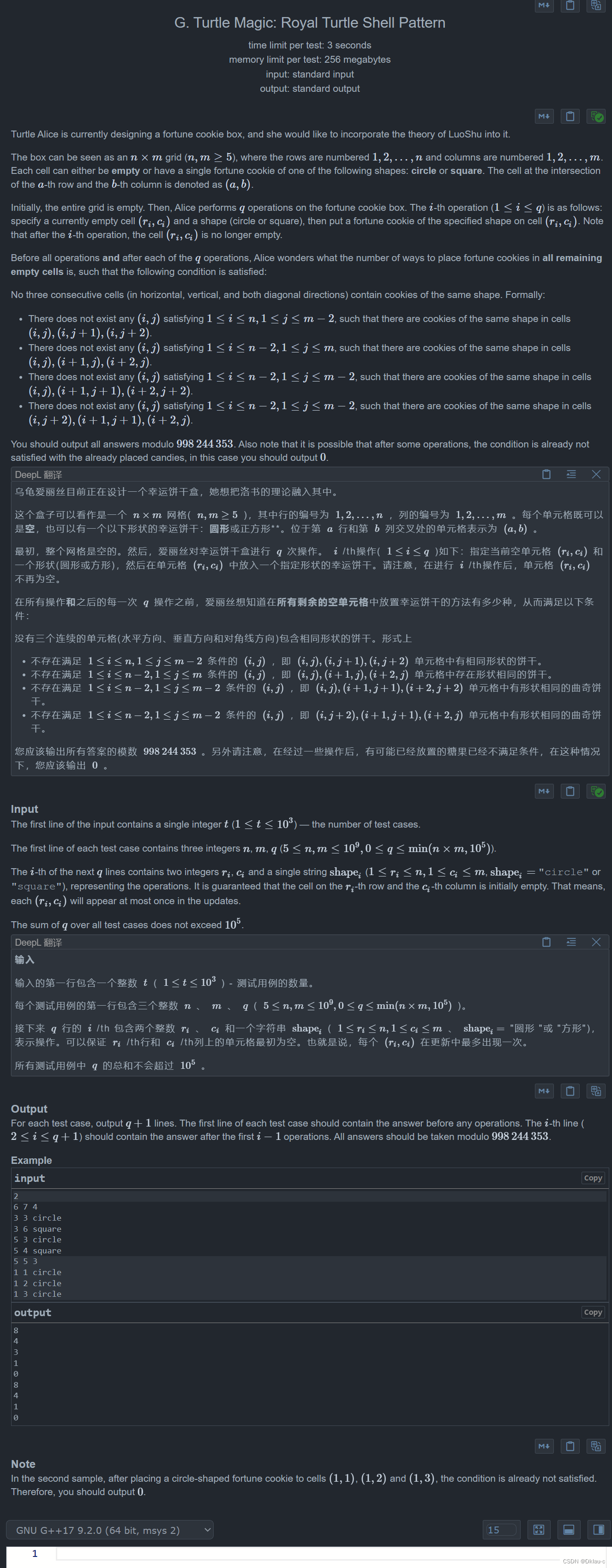
}G题:Turtle Magic: Royal Turtle Shell Pattern
 思路:
思路:
我们思考可以发现,如果我们想要不违反规定的话,我们就必须要间隔的放这两种饼干,但如果只间隔1个饼干即(0101010)这样放的话,就会违反第三条规定,对角线重合,所以我们需要间隔两个饼干放即(001100)这样放就不会冲突了。
我们观察样例发现,在没有放饼干的时候,输出是8 也就是意味着饼干不冲突的放法最大为8,横着的001100 这样4种竖着也4种,所以8种,于是我们就可以将输入的位置带入到这8种情况种,如果有不符合条件的就让答案减1,最后输出符合情况的个数即可。
如有不懂还可以看这个视频,讲解。
代码;
#include <iostream>
using namespace std;
int find(int x,int y,int k)
{
if(k<4)
{
y+=k; //增加偏移量
if(x%2==1) return y%4==0 || y%4==3; //奇数行
else return y%4==1 || y%4==2; //偶数行,每一元素与奇数行相反
}
else
{
x+=k-4;
if(y%2==1) return x%4==0 || x%4==3;
else return x%4==1 || x%4==2;
}
}
void solve()
{
int n,m,q;
cin>>n>>m>>q;
cout<<8<<endl;
int flag[10]={0};
int ans=8;
while (q--)
{
int x,y;
string str;
cin>>x>>y>>str;
int t=str[0]=='s'; //shape 为1 反之则为0
for(int i=0;i<8;i++)
{
if(flag[i]==0)
{
if(find(x,y,i)!=t)
{
flag[i]=1;
ans--;
}
}
}
cout<<ans<<endl;
}
}
int main()
{
int t;
cin>>t;
while (t--) solve();
return 0;
}




![[数据结构]队列](https://img-blog.csdnimg.cn/direct/dc8dd37d010f4e46a608d3dcac720b19.png)