背景

这里举一个简单的情况，当前我们有p1, p2, p3三个概率，我们需要得到最优的一个即max(p1, p2, p3)，例如当前p3 = max(p1, p2, p3)，那么理想输出应当为[0, 0, 1]，然后应用于下游的优化目标，这种场景在搜索等场景经常出现。
如果暴力的进行clip或者mask操作转化为独热向量的话会导致在梯度反向传播的时候无法更新上游网络。因为p1和p2对应的梯度一定为0。

方法通俗理解

针对上述情况，采用重参数化的思路可以解决。
即然每次前向传播理想情况下是0-1独热向量向量，但同时能保证[p1, p2, p3]这个分布能被根据概率被更新。于是采用了一种重参数化的方法，即从每次都从一个分布中采样一个u，这个u属于一个均匀分布，从这个均匀分布通过转换变成[p1, p2, p3]这个分布。这样就能即保证梯度可以反向传播，同时根据每次采样来实现按照[p1, p2, p3]这个分布更新，而不是每次只能更新最大的一个。
而这种方法就是重参数化。

什么是重参数化

Reparameterization，重参数化，这是一个方法论，是一种技巧。
我们首先可以抽象出来它的数学表达形式：
$$\begin{array}{c}{L}_{\theta }=E_{z～p_{{\theta }^{\prime }}(z)}(f_{\theta }(z))\end{array}$$
注意：在有些时候${\theta }^{\prime }\in \theta$或者${\theta }^{\prime }=\theta$。
如何理解：这里我们的优化目标是$L_{\theta }$，其中$f_{\theta }()$一般是我们的模型，而计算$z$是从分布$p_{{\theta }^{\prime }}(z)$中采样得到的。但是问题是我们不能把一个分布输入到$f_{\theta }()$中去，只能从选择一个特定的$z$，但是这样就没法更新${\theta }^{\prime }$。
综上，重参数化就是从给定分布中采样得到一个$z$，同时保证了梯度可以更新${\theta }^{\prime }$，这种保证采样分布和给定分布无损转换的采样策略叫做重参数化。（个人理解，欢迎大佬指正）

由于我们现在解决的是gumbel-softmax问题，所以只关注当$p_{{\theta }^{\prime }}(z)$是离散的情况下，此时：
$$\begin{array}{c}{L}_{\theta }=E_{z～p_{{\theta }^{\prime }}(z)}(f_{\theta }(z))=\sum p_{{\theta }^{\prime }}(z)(f_{\theta }(z))\end{array}$$
这也就是gumbel-softmax要解决的数学形式。

gumbel-softmax

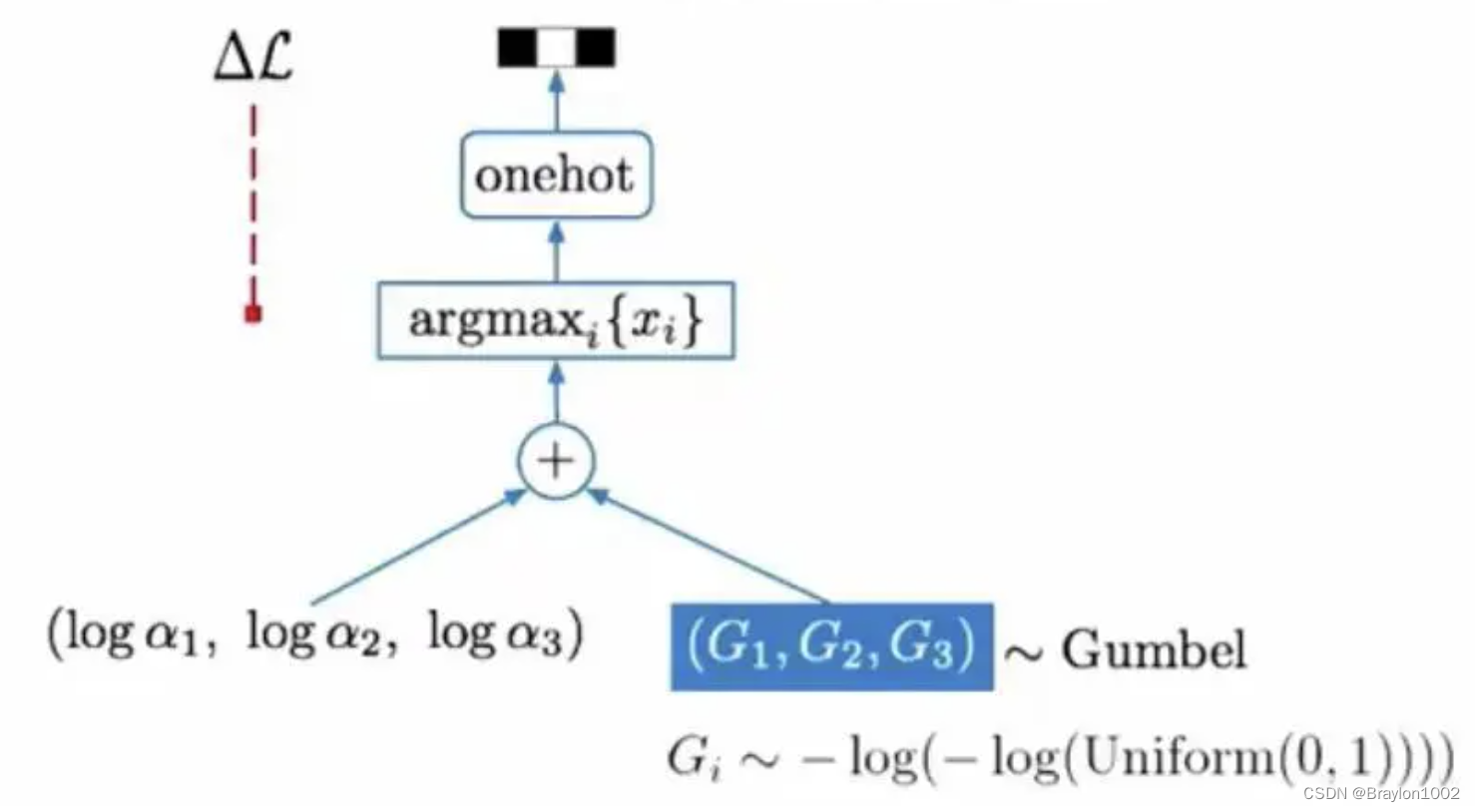
gumbel-softmax给出的采样方案，叫做gumbel max：
从原来的$argma{x}_i([p1,p2,...])$到$argma{x}_i(log(p_i)-log(-log({ϵ}_i))),{ϵ}_i\in U[0,1]$

也就是先算出各个概率的对数$log(p_i)$，然后从均匀分布$U$中采样随机数${ϵ}_i$，把$-log(-log{ϵ}_i)$加到$log(p_i)$，然后再进行后续操作。
这里可以理解为通过$ϵ$的采样将随机性增加。有的人会疑问，为什么格式变得这么复杂，各种算log，这是为什么？这个就涉及到下一节了，具体原因就是来保证数学的变换正确性，即我增加了随机性，但是保证分布的期望仍然是和原始[p1, p2, p3]是一致的，这个证明在下一节，是有比较严谨的数学证明的。

但是这里还有一个问题，就是argmax或者说onehot操作仍然会丢失梯度，所以采用带超参$\tau$的softmax，来进行平滑：
$$\begin{array}{c}softmax((log(p_i)-log(-log({ϵ}_i)))/\tau )\end{array}$$
其中$\tau$也被称为退火参数，用来调整平滑的程度：$\tau$越小，越接近onhot向量。

这里也解释清楚了所谓gumbel-softmax是通过gumbel max实现重参数化，通过带退火参数的softmax实现梯度反向传递。

为什么是gumbel

这就涉及到一个gumbel max的证明了。
目标是证明针对$log(p_i)-log(-log({ϵ}_i))$，当$argma{x}_i(log(p_i)-log(-log({ϵ}_i)))=1$时，其概率为$p_1$。

假设：
$log(p_1)-log(-log({ϵ}_1))$ 最大

则：
$log(p_1)-log(-log({ϵ}_1))>log(p_2)-log(-log({ϵ}_2))$
$log(p_1)-log(-log({ϵ}_1))>log(p_3)-log(-log({ϵ}_3))$
…

$log(p_1)-log(-log({ϵ}_1))>log(p_2)-log(-log({ϵ}_2))$ ->
${ϵ}_1^{p_2/p_1}>{ϵ}_2$
所以： $p1$ 大于 $p_2$ 的概率是${ϵ}_1^{p_2/p_1}$

同理：
$p1$ 大于 $p_3$ 的概率是${ϵ}_1^{p_3/p_1}$
…

所以$log(p_1)-log(-log({ϵ}_1))$ 最大的概率是：
${ϵ}_1^{p_2/p_1}$ * ${ϵ}_1^{p_3/p_1}$ * … = ${ϵ}_1^{(1-p_1)/p_1}$
$E({ϵ}_1^{(1-p_1)/p_1})$ = ${\int }_0^1{ϵ}_1^{(1-p_1)/p_1}dϵ$ = ${\int }_0^1{ϵ}_1^{(1/p_1)-1}d{ϵ}_1$ = $(p_1({ϵ}_1^{1/p_1})){|}_0^1$ = $p_1$

证明假设成立

torch实现

def sample_gumbel(shape, eps=1e-20):
    U = torch.rand(shape)
    U = U.cuda()
    return -torch.log(-torch.log(U + eps) + eps)


def gumbel_softmax_sample(logits, temperature=0.5):
    y = torch.log(logits) + sample_gumbel(logits.size())
    return F.softmax(y / temperature, dim=-1)


def gumbel_softmax(logits, temperature=1, hard=False):
    """
    input: [B, n_class]
    return: [B, n_class] an one-hot vector
    """
    y = gumbel_softmax_sample(logits, temperature)
    
    if not hard:
        return y

    shape = y.size()
    _, ind = y.max(dim=-1)
    y_hard = torch.zeros_like(y).view(-1, shape[-1])
    y_hard.scatter_(1, ind.view(-1, 1), 1)
    y_hard = y_hard.view(*shape)
    # Set gradients w.r.t. y_hard gradients w.r.t. y
    y_hard = (y_hard - y).detach() + y
    return y_hard

思考

为什么gumbel-softmax和softmax的输出是不一样的？
为什么argmax(gumbel-softmax) 和 argmax(softmax)的结果也不一定一样？这是正常的吗？

大家共勉～