参考：https://blog.csdn.net/weixin_44259490/article/details/90295146

概念

梯度与w的关系可以用梯度下降公式来表示：w=w−α$\frac{\partial cost}{\partial w}$，其中w表示网络的权重，$\frac{\partial cost}{\partial w}$表示损失函数对权重w的导数，即梯度，α为学习率。

w=w−α$\frac{\partial cost}{\partial w}$

梯度下降是一种常用的优化算法，用于更新网络的权重和偏置，以最小化损失函数。

案例

一个神经网络包括很多神经元，每个神经元都有参数w、b，所以每个神经元都对应有对w、b的梯度，然后更新w、b

简单案例参考：

w的梯度：

更新梯度： w = w - eta * dw

求b的梯度

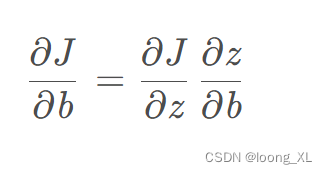
更新梯度： b = b - eta * db

梯度与导数关系

梯度与导数关系：
导数和梯度都是微积分中的重要概念，它们之间存在密切的联系。

导数是函数在某一点处的切线斜率，它表示函数在该点处的变化率。对于一个函数f(x)，它在点x_0处的导数可以表示为f^\prime(x_0)。
梯度是一个向量，它表示函数在某一点处的最大变化率方向。对于一个多元函数f(x_1,x_2,\cdots,x_n)，它在点(x_1,x_2,\cdots,x_n)处的梯度可以表示为\nabla
f(x_1,x_2,\cdots,x_n)。
在一元函数的情况下，导数和梯度是等价的，因为函数在某一点处的导数就是该点处切线的斜率，也就是函数在该点处的梯度方向。
在多元函数的情况下，导数是一个标量，而梯度是一个向量。梯度的方向是函数在该点处变化最快的方向，其大小表示函数在该方向上的变化率。导数可以看作是梯度在某个特定方向上的分量。
在优化问题中，梯度扮演着重要的角色。梯度下降法是一种常用的优化算法，它通过沿着函数的梯度方向移动来找到函数的最小值。
总的来说，导数和梯度都是描述函数变化率的概念，导数是标量，而梯度是向量。在多元函数的情况下，梯度提供了函数在各个方向上的变化信息，对于优化问题和数据分析等领域具有重要的应用。