波动方程初值问题能量不等式的证明

Gronwall 不等式

若非负函数 $G(\tau )$ 在$[0,T]$ 上连续可微，$G(0)=0$，且对 $\tau \in [0,T]$满足 $$\frac{dG(\tau )}{d\tau }\le CG(\tau )+F(\tau )$$ 其中 $C$ 为常数且 $C>0$，$F(\tau )$ 是$[0,T]$ 上不减的非负可积函数，

那么有：

$$\frac{dG(\tau )}{d\tau }\le e^{C\tau }F(\tau )$$ $$G(\tau )\le C^{-1}(e^{C\tau }-1)F(\tau )$$

常用的替换技巧

$$u_t{u}_{tt}=\frac{1}{2}\cdot 2u_t\cdot u_{tt}=\frac{1}{2}(u_t^2{)}_t$$$$u{u}_t=\frac{1}{2}\cdot 2u\cdot u_t=\frac{1}{2}(u^2{)}_t$$$$u{u}_{xx}=(u{u}_x{)}_x-u_x^2=u_x^2+u{u}_{xx}-u_x^2$$$$\because (u_t{u}_x{)}_x=u_{tx}{u}_x+u_t{u}_{xx}$$$$\therefore u_t{u}_{xx}=(u_t{u}_x{)}_x-u_{tx}{u}_x$$

$u$ 二阶导函数连续时，$$u_{xt}=u_{tx}$$$$\therefore u_{tx}{u}_x=\frac{1}{2}(u_x^2{)}_t=\frac{1}{2}\cdot 2u_x\cdot u_{xt}=u_x{u}_{tx}$$$$\therefore u_t{u}_{xx}=(u_t{u}_x{)}_x-\frac{1}{2}(u_x^2{)}_t$$

能量不等式证明过程

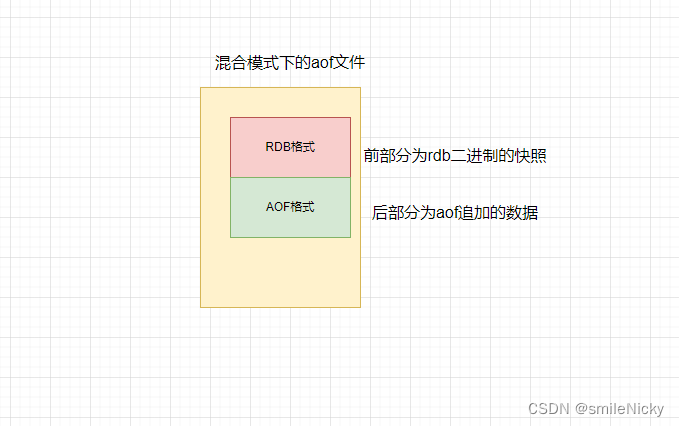
规定 $x$ 增长的方向为正方向，而 $Green$ 公式曲线积分时，组成梯形区域 $K_{\tau }$ 边界 $\partial K_{\tau }$ 的四条线段按照右手法则，只有 ${\Omega }_0$ 这条线段的方向是与右手法则一致，所以有：

$\partial K_{\tau }={\Omega }_0\cup (-{\Gamma }_{{\tau }_2})\cup (-{\Omega }_{\tau })\cup (-{\Gamma }_{{\tau }_1})$

此外，在 $\partial K_{\tau }$ 计算曲线积分时，关于 $x,t$ 都积分，但是这两条边 ${\Omega }_0,{\Omega }_{\tau }$ 只在 $x$ 方向有增长，而在 $t$ 方向无增长，那么这两条线段在计算曲线积分时关于 $dt$ 的积分项为 $0$

待证明的两个不等式：
$${\int }_{{\Omega }_{\tau }}\left[u_t^2(x,\tau )+a^2{u}_x^2(x,\tau )\right]dx\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$$${\int }_{K_{\tau }}\left[u_t^2(x,t)+a^2{u}_x^2(x,t)\right]dxdt\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$

1. 在波动方程 $\frac{{\partial }^{2}u}{\partial t^2}-a^2\frac{{\partial }^{2}u}{\partial x^2}=f$ 两端同乘以 $\frac{\partial u}{\partial t}$ 并在区域 $K_{\tau }$ 上积分并按照前面的常用替换得：

${\iint }_{K_{\tau }}{u}_t{u}_{tt}-a^2{u}_t{u}_{xx}dxdt={\iint }_{K_{\tau }}ufdxdt$$

${\iint }_{K_{\tau }}\frac{1}{2}(u_t^2+a^2{u}_x^2{)}_t-a^2(u_t{u}_x{)}_{x}dxdt={\iint }_{K_{\tau }}ufdxdt$

2. 应用下面这个 $Green$ 公式将上面等式左边替换
   $${\iint }_{\Omega }\frac{\partial P}{\partial t}+\frac{\partial Q}{\partial x}d\sigma ={\oint }_{\partial \Omega }-Pdx+Qdt$$其中 $P=\frac{1}{2}(u_t^2+a^2{u}_x^2)$， $Q=-a^2(u_t{u}_x)$，得闭合曲线积分

${\oint }_{\partial K_{\tau }}[-\frac{1}{2}(u_t^2+a^2{u}_x^2)dx-a^2(u_t{u}_x)dt]$

$=-{\oint }_{\partial K_{\tau }}{a}^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

记 $a^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx=\square$，

$\because \partial K_{\tau }={\Omega }_0\cup (-{\Gamma }_{{\tau }_2})\cup (-{\Omega }_{\tau })\cup (-{\Gamma }_{{\tau }_1})$

$\therefore -{\oint }_{\partial K_{\tau }}{a}^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

$=-[{\int }_{{\Omega }_0}\square -{\int }_{{\Omega }_{\tau }}\square -{\int }_{{\Gamma }_{{\tau }_1}}\square -{\int }_{{\Gamma }_{{\tau }_2}}\square ]$

${\Omega }_0,{\Omega }_{\tau }$ 只在 $x$ 方向有增长，而在 $t$ 方向无增长，那么这两条线段在计算曲线积分时关于 $dt$ 的积分项为 $0$，可得

$-{\oint }_{\partial K_{\tau }}{a}^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

$={\int }_{{\Gamma }_{{\tau }_1}\cup {\Gamma }_{{\tau }_2}}{a}^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx-{\int }_{{\Omega }_0}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx+{\int }_{{\Omega }_{\tau }}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

记上面等式的三项分别为 $J_1,J_2,J_3$，即：

$J_1={\int }_{{\Gamma }_{{\tau }_1}\cup {\Gamma }_{{\tau }_2}}{a}^2(u_t{u}_x)dt+\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

$J_2=-{\int }_{{\Omega }_0}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

$J_3={\int }_{{\Omega }_{\tau }}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$

3. 应用下面 $dx$ 和 $dt$ 的关系，将 $J_1$ 统一为只关于 $dt$ 的积分
   $${\Gamma }_{{\tau }_1}:dx=adt$$$${\Gamma }_{{\tau }_2}:dx=-adt$$

即$J_1={\int }_{{\Gamma }_{{\tau }_1}}{a}^2(u_t{u}_x)dt+\frac{1}{2}a(u_t^2+a^2{u}_x^2)dt+{\int }_{{\Gamma }_{{\tau }_2}}{a}^2(u_t{u}_x)dt-\frac{1}{2}a(u_t^2+a^2{u}_x^2)dt$
$={\int }_{{\Gamma }_{{\tau }_1}}\frac{a}{2}(2a{u}_t{u}_x+u_t^2+a^2{u}_x^2)dt+{\int }_{{\Gamma }_{{\tau }_1}}\frac{a}{2}(2a{u}_t{u}_x-u_t^2-a^2{u}_x^2)dt$

利用完全平方公式得

$J_1={\int }_{{\Gamma }_{{\tau }_1}}\frac{a}{2}(u_t+a{u}_x{)}^{2}dt-{\int }_{{\Gamma }_{{\tau }_2}}\frac{a}{2}(u_t-a{u}_x{)}^{2}dt$

因为在 ${\Gamma }_{{\tau }_1}$ 线段上规定的正方向是 $t$ 增长的方向，而 ${\Gamma }_{{\tau }_2}$ 上相反，所以 $t$ 的积分限分别是 $0$ 到 $\tau$ 和 $\tau$ 到 $0$ ，也即

$J_1={\int }_0^{\tau }\frac{a}{2}(u_t+a{u}_x{)}^{2}dt-{\int }_{\tau }^0\frac{a}{2}(u_t-a{u}_x{)}^{2}dt\ge 0$

第一项平方项且积分下限小于上限故其积分非负，而第二项是平方项在积分下限大于上限加上前面的负号，故也是非负，所以 $J_1\ge 0$

4. 把 $J_1,J_2,J_3$ 写回来，根据 $J_1\ge 0$ 构造不等关系
   $$J_1+J_2+J_3={\iint }_{K_{\tau }}{u}_{t}fdxdt$$
   $\because J_1\ge 0$
   $$\therefore J_3\le J_1+J_3=J_1+J_2+J_3-J_2={\iint }_{K_{\tau }}{u}_{t}fdxdt-J_2$$
   也即 $${\int }_{{\Omega }_{\tau }}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}{u}_{t}fdxdt+{\int }_{{\Omega }_0}\frac{1}{2}(u_t^2+a^2{u}_x^2)dx$$
   两边同乘 $2$ 且 ${\Omega }_0$ 是 $t=0$ 的线段，而 $t=0$ 时，$u_t(x,0)=\psi ,u_x(x,0)={\phi }_x$即
   $${\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}2u_{t}fdxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$$

对上面不等式右边 ${\iint }_{K_{\tau }}2u_{t}fdxdt$ 这一项应用 $Cauchy$ 不等式 $2ab\le a^2+b^2$ 得
$${\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}{u}_t^2+f^{2}dxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$$

此时，对比要证明的不等式
$${\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}{f}^{2}dxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$$
发现只是右端多了一项 ${\iint }_{K_{\tau }}{u}_t^{2}dxdt$

5. 利用 $Gronwall$ 不等式将该项消去

令 $G(\tau )={\iint }_{K_{\tau }}(u_t^2+a^2{u}_x^2)dxdt={\int }_0^{\tau }{\int }_{x_0-a(t_0-t)}^{x_0+a(t_0-t)}(u_t^2+a^2{u}_x^2)dxdt$

则 $\frac{dG(\tau )}{d\tau }={\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx$ 是待证明不等式的左端

令 $F(\tau )={\iint }_{K_{\tau }}{f}^{2}dxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$

给 $${\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}{u}_t^2+f^{2}dxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$$ 右边添加${\iint }_{K_{\tau }}{a}^2{u}_x^{2}dxdt$，则
$${\int }_{{\Omega }_{\tau }}(u_t^2+a^2{u}_x^2)dx\le {\iint }_{K_{\tau }}{u}_t^2+a^2{u}_x^2+f^{2}dxdt+{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx$$

那么此时该不等式满足 $Gronwall$ 不等式的前提条件
$$\frac{dG(\tau )}{d\tau }\le CG(\tau )+F(\tau )$$
此时 $C=1$，那么由 $Gronwall$ 不等式的两个结论，可分别得到如下两个能量不等式，其中 $M=e^{\tau }$
$${\int }_{{\Omega }_{\tau }}\left[u_t^2(x,\tau )+a^2{u}_x^2(x,\tau )\right]dx\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$
$${\int }_{K_{\tau }}\left[u_t^2(x,t)+a^2{u}_x^2(x,t)\right]dxdt\le M\left[{\int }_{{\Omega }_0}({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{K_{\tau }}{f}^2(x,t)dxdt\right]$$

波动方程混合问题能量不等式的证明

待证明的两个不等式：
$${\int }_0^l\left[u_t^2(x,\tau )+a^2{u}_x^2(x,\tau )\right]dx\le M\left[{\int }_0^l({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{Q_{\tau }}{f}^{2}dxdt\right]$$$${\iint }_{Q_{\tau }}\left(u_t^2+a^2{u}_x^2\right)dxdt\le M\left[{\int }_0^l({\psi }^2+a^2{\phi }_x^2)dx+{\int }_{Q_{\tau }}{f}^{2}dxdt\right]$$

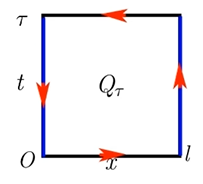
二维区域的情况下，这里可以不用 $Green$ 公式将面积分转为线积分，可以直接按照二重积分展开。

1. 在波动方程 $u_{tt}-a^2{u}_{xx}=f$ 两端同乘 $u_t$ 并在区域 $Q_{\tau }=(0,l)\times (0,\tau )$ 上积分

${\iint }_{Q_{\tau }}{u}_t{u}_{tt}-a^2{u}_t{u}_{xx}dxdt={\iint }_{Q_{\tau }}{u}_{t}fdxdt$

利用常用的替换技巧
$$u_t{u}_{tt}=\frac{1}{2}\cdot 2u_t\cdot u_{tt}=\frac{1}{2}(u_t^2{)}_t$$$$u_t{u}_{xx}=(u_t{u}_x{)}_x-\frac{1}{2}(u_x^2{)}_t$$得${\iint }_{Q_{\tau }}\frac{1}{2}(u_t^2{)}_t+\frac{1}{2}{a}^2(u_x^2{)}_t-(a^2{u}_t{u}_x{)}_{x}dxdt$，这里用二重积分展开

${\iint }_{Q_{\tau }}\frac{1}{2}(u_t^2{)}_t+\frac{1}{2}{a}^2(u_x^2{)}_t-(a^2{u}_t{u}_x{)}_{x}dxdt$

$={\int }_0^{\tau }{\int }_0^l[(\frac{1}{2}{u}_t^2+\frac{1}{2}{a}^2{u}_x^2{)}_t-(a^2{u}_t{u}_x{)}_x]dxdt$

$$={\int }_0^l\frac{1}{2}{u}_t^2(x,\tau )+\frac{1}{2}{a}^2{u}_x^2(x,\tau )dx-{\int }_0^l\frac{1}{2}{u}_t^2(x,0)+\frac{1}{2}{a}^2{u}_x^2(x,0)dx-{\int }_0^{\tau }{a}^2{u}_t(l,t)u_x(l,t)dt+{\int }_0^{\tau }{a}^2{u}_t(0,t)u_x(0,t)dt$$

2. 根据初始条件和齐次边界条件替换上面表达式

初始条件：
$$u_t(x,0)=\psi (x)$$$$u_x(x,0)={\phi }_x(x)$$
边界条件：
$$u(0,t)=0$$$$u(l,t)=0$$即杆的两端是固定的，也即速度为 $0$
$$u_t(l,t)=u_t(0,t)=0$$ 带入 $1.$ 得到的等式并两边同乘 $2$ 得

$$={\int }_0^l{u}_t^2(x,\tau )+a^2{u}_x^2(x,\tau )dx={\int }_0^l{\psi }^2+a^2{\phi }_x^{2}dx+2{\int }_0^{\tau }{\int }_0^l{u}_{t}fdxdt$$
对等式右边应用 $Cauchy$ 不等式以及添加非负项 ${\int }_0^{\tau }{\int }_0^l{a}^2{u}_x^{2}dxdt$ 得

$${\int }_0^l{u}_t^2(x,\tau )+a^2{u}_x^2(x,\tau )dx\le {\int }_0^l{\psi }^2+a^2{\phi }_x^{2}dx+{\int }_0^{\tau }{\int }_0^l{f}^{2}dxdt+{\int }_0^{\tau }{\int }_0^l{u}_t^2+a^2{u}_x^{2}dxdt$$

3. 应用 $Gronwall$ 不等式

令 $G(\tau )={\int }_0^{\tau }{\int }_0^l{u}_t^2+a^2{u}_x^{2}dxdt$

$F(\tau )={\int }_0^l{\psi }^2+a^2{\phi }_x^{2}dx+{\int }_0^{\tau }{\int }_0^l{f}^{2}dxdt$

那么 $\frac{dG(\tau )}{d\tau }={\int }_0^l{u}_t^2(x,\tau )+a^2{u}_x^2(x,\tau )dx$

将 $G(\tau ),F(\tau ),\frac{dG(\tau )}{d\tau }$ 带入 $Gronwall$ 不等式的两个结论即得到待证不等式，其中 $C=1$