之前我们学习的线性回归算法,适用于预测值y为连续值的情况下,但是在分类问题中,预测值y是个离散值,所以线性回归算法不适用。在这篇文章中,主要以二分类问题为例,介绍分类算法————logistic回归算法(之所以叫回归,据说是历史原因,但实际上和回归算法没关系,它是一个分类算法)。
所谓的二分类算法,就是预测值y只有两种结果,这里以0和1分别表示这两种结果。
logistic分类算法
假设函数
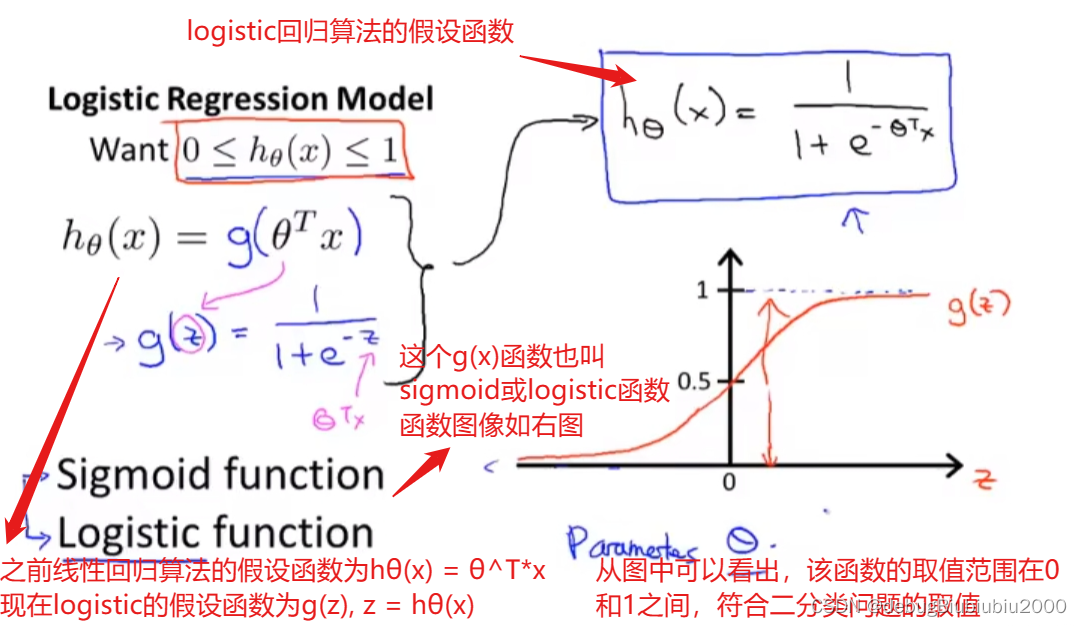
假设函数如下,得到假设函数之后,下一步也是根据训练集数据确定θ的值,然后得到一个最合适的假设函数去拟合数据
假设函数h(x)输出值的含义:logistic回归算法的假设函数输出值表示的是预测值y=1的概率(当然,也可以计算y=0的概率,这两个其实都一样,因为y只能等于0或者1,所以两者概率相加等于1:P(y=0) + P(y=1) = 1,知道了其中任一个都能得到另一个),比如在确定了某个θ的值,θ=0.35,输入x=2,h(2)=0.7,就表示在输入x=2的情况下,y=1的概率为百分之七十,也就是x=2这个样本是属于1那种分类

决策边界的概念
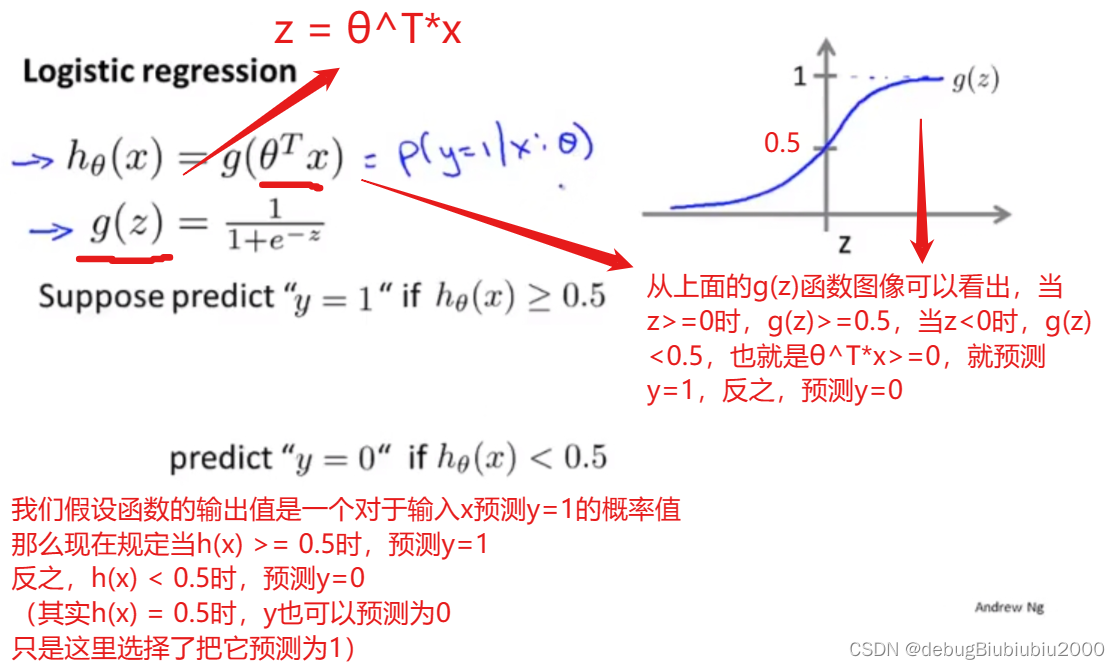
决策边界,我的理解就是以确定一个边界,来决策一个问题的答案,如下图中,确定了边界0.5,当假设函数的值大于等于0.5时,决策y=1这一答案
利用边界决策的概念理解假设函数预测过程,如下
 举例,如下
举例,如下

更复杂的决策边界例子,如下


说明:决策边界不是训练集的属性,而是假设函数的属性,只要确定了参数θ的值,进而确定了假设函数,那么就可以得到一个确定的决策边界,与训练集数据无关
代价函数
插播一下:代价函数指的就是预测值和真实值之间的差值,这个差值就称为代价,那么我们希望这个代价为0,也就是预测值和真实值完全一样,但是这不太可能,所以退而求其次,努力让这个代价降到最小,所以就是求代价函数值最小时的θ值,然后就可以得到最优的假设函数,也就是最拟合训练集数据的假设函数。
我们知道,代价函数用于选择最优的θ参数,所以我们现在来说如何确定θ参数

单训练样本的代价函数
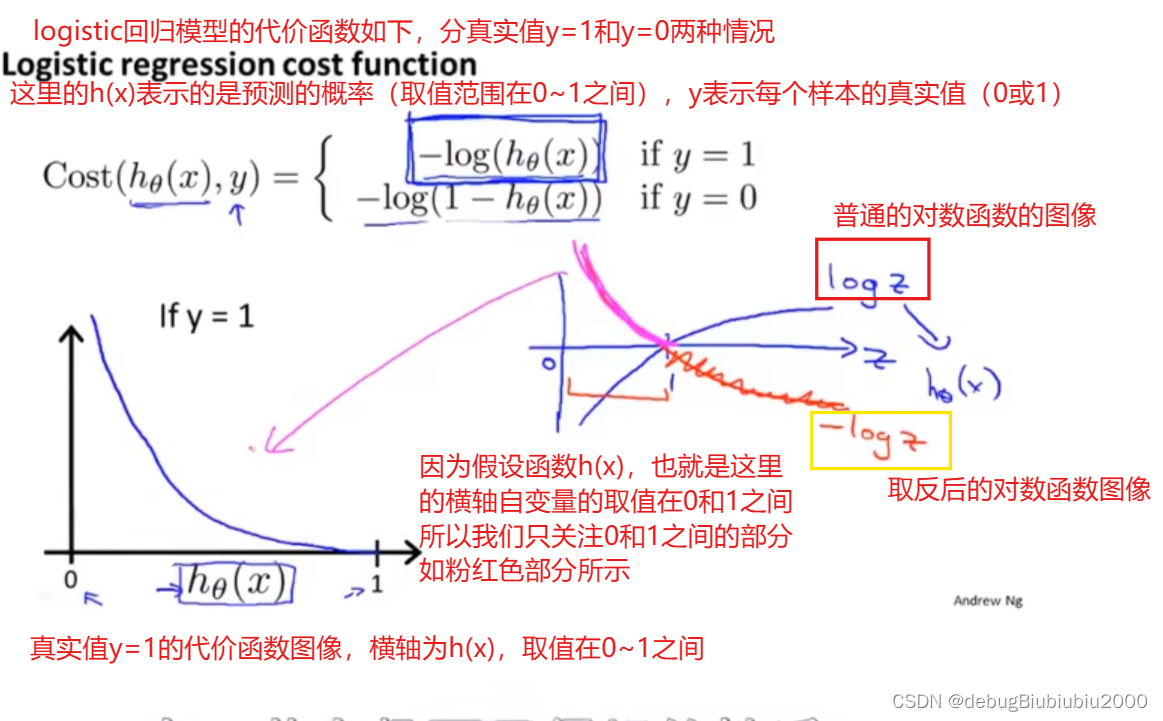
针对单个样本的代价函数如下

整个训练集的代价函数

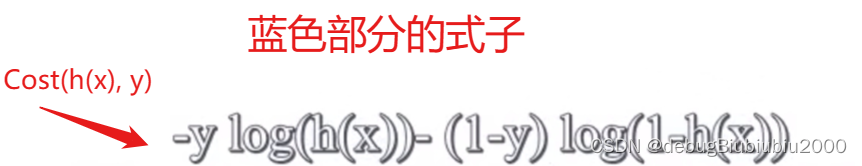

梯度下降算法求θ参数值
确定了代价函数,接下来就是求最小的代价函数值时的θ,下面采用梯度下降法最小化代价函数



其他最小化代价函数的高级优化算法
除了梯度下降算法以外,还有其他更高效的算法可以最小化代价函数,且比梯度下降算法更高效。这些高级优化算法不进适用于logistic回归,也适用于线性回归。
算法的具体使用方法参考视频(不好记笔记,还是直接看视频直观):高级优化算法
 多分类问题
多分类问题
所谓的多分类问题,就是y是个离散值,且y的取值有两种以上的可能,比如y的取值可能为【1,2,3,4】中的某一个
求解多分类问题看视频(也不爱做笔记了):多分类问题