《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》

本人能力有限，如果错误欢迎批评指正。

第四章：Protein Binding Leads to Biological Actions

（蛋白质的结合会产生生物作用）

如果我们想要对一个结合过程进行建模，那么我们首先要做的就是构建它的结合多项式。一般来说，我们可以通过简单的方式来写出各种平衡的具体步骤。而在这个过程中，我们可以使用概率挥着中的乘法和加法。如果有两个状态是相斥的(结合或者解绑)，我们可以计算他们的统计权重。使用1作为非绑定状态的统计权重（因为我们将所有其他状态都相对于它），使用Kx作为绑定状态的统计权重，最后我们可以获得单个位点结合时的Q = 1 + Kx。相似的，根据乘法规则，如果两个配体独立结合，那么对结合多项式的贡献是两个统计权值的乘积。例如，对于两个独立的位点，Q =（1 + Kax）（1 + Kbx）。方框4.1展示了如何建模n个独立的站点。

到目前为止，我们只描述了配体的结合平衡。但通常结合平衡也是动力学的基础。某些反应的速率取决于配体与一个位点的结合量。例如，在下面描述的米曼氏动力学(Michaelis–Menten kinetics)中，当底物的浓度足够高，使其与蛋白质位点的结合饱和时，反应达到其最大速度。

如酶催化或分子穿过蛋白质通道的速率过程可以被模拟城两个步骤：首先是将配体与蛋白质结合的平衡步骤，然后是动力学步骤。在转化过程之前，我们可以想象一下一个由P进行催化的底物X转化为Z进行结合过程：

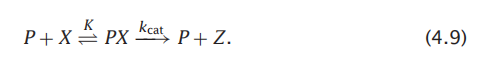
这各过程称为米曼氏动力学。其中，PX只的是酶与底物的节后然后X为产物。图4.2展示了该机制中随着时间[P],[X],[PX]浓度的变化。

图4.2 米曼氏动力学过程随着时间的过程，显示了底物随着时间的推移而耗尽，产物的增加，以及整个过程中的小浓度[PX]。

假设速率常数kcat足够小，足以使底物与酶的结合（第一个反应）达到平衡。平衡常数为

式中，x = [X]为底物浓度，[PX]为酶-底物复合物PX的浓度，[P]为游离酶的浓度。酶催化反应的速率原则上是Z、dZ/dt的生产速率，也称为速率v：

无论是结合的还是非结合的状态，酶分子在反应的总数中是保守的：

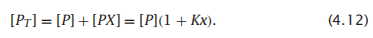
因此我们可以用可测量的常数来表示v，这样子可以避免去计算难以测量的[PX],你可以用公式4.11除以公式4.12得到每个酶分子的速率：

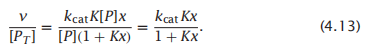
当酶被底物完全饱和时，产物的形成速度最快：Kx/(1 + Kx) = 1。则最大速率为vmax = kcat[PT]。用vmax表示，反应速率为：

其中，最后一个等式用解离常数Kd = 1/K表示。

方程4.14显示了由于潜在结合步骤中的饱和，酶催化反应的最大速率（动力学饱和）（图4.3）

图4.3 米曼氏动力学：随着底物浓度随着反应速率不断增加直至饱和。产物的产生速率随着底物浓度的增加而增加，直到以最大速度饱和。Km是反应速度等于最大速度的一半时底物的浓度。

底物必须与酶结合后才能催化反应。如果溶液中底物的浓度足够高，它就会填满可用的酶位点，因此反应会受到酶浓度的限制。有时，公式4.14也表示为

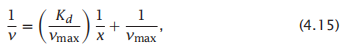
而这可以将数据绘制成一条直线，从1/v与1/x的线性关系，其中斜率为Kd/vmax，截距将是1/vmax。这种图被称为双倒数图(Lineweaver–Burk or double-reciprocal)。如今，从实验数据中提取Kd和vmax等参数的更好方法是使用标准的计算机软件包来解释数据点中的错误。请注意，米曼氏动力学并不是最好的变构酶动力学模拟方式；这些酶的模型将在本章后面描述。

米曼氏动力学并不局限于酶催化。它也通常可用于处理其他过程。例如，有时配体分子X可以与膜蛋白通道结合，打开该通道，增加离子或小分子通过该通道的流量。在高浓度的X时，所有的通道都被束缚住了，所以所有的通道都是开放的，并且流量最大的。另一个例子见方框4.2。

我们已经可以描述由于结合过程导致的反应速率。只要结合步骤本身足够快，可以在最后一个较慢的动力学步骤之前达到平衡。但假设我们对某些过程的结合动力学本身感兴趣。药物发现者有时想知道一种结合了蛋白的药物解离速率(off-rate)。解离率是衡量药物与蛋白质结合时间，这通常是衡量药物生物有效性的关键指标。那么我们如何模拟结合和解离的动力学？考虑一个配体结合到一个位点，P + X→PX。在某些情况下，结合的动力学可以简单地用双态动力学来模拟：

其中，两个速率参数kon和koff分别表示结合和解离速率。在第6章中，我们描述了如何将这样的模型表示为微分方程，从而给出反应的时间依赖性。现在，我们只是注意到这个双态模型体现单指数动力学。因此，如果你观察到结合和解离的单指数动力学，那么这个双态模型进行模拟是足够的，并且我们可以通过拟合数据来获得解离率和结合率之间的关系。然而，在其他的结合过程中，双态动力学机制的描述过于简单。事实上，你可以观察到结合动力学比单指数的模拟更复杂。因此，为了从实验数据中推断速率，我们必须使用更多的动力学状态和更多的参数来拟合速率曲线。

两种最著名的蛋白质-配体结合机制被称为诱导匹配和构象选择（图4.5）。在诱导匹配机制中，配体首先与蛋白质结合，然后蛋白质重新调整其构象以适应配体。在构象选择机制中，蛋白质取样的是一个构象的集合，配体选择了在结合时允许最有利的相互作用的构象。这两种机制在图4.5中显示为从非束缚态到束缚态的两种不同的动力学路径。

图4.5诱导拟合与构象选择。在诱导匹配机制中，配体首先结合，然后调整蛋白质的构象。在构象选择中，蛋白质填充了一系列构象，配体与一个选定的构象结合。

其中，构象选择机制可以模拟为：

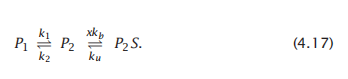
该机制需要四个参数：k1、k2、ku和kb。量x表示第二次反应的正向速率也取决于配体x的浓度。另外，这种两步反应的一个变体可以表达诱导拟合机制。或者配体可以通过组合或其他机制结合。研究结合机制的结构基础是一个流行的研究领域，在第12章中描述。

-------------------------------------------

欢迎点赞收藏转发！

下次见！