一：损失函数

损失函数（loss function）：深度学习中所有算法的目标都是为了最小化或最大化一个函数，称之为损失函数或者是目标函数、代价函数，损失函数是衡量模型的效果苹果

在深度学习中损失函数可以分为如下两类

• 回归损失：适用于回归问题，典型代表是均方误差（MSE）
• 分类损失：适用于分类问题，典型代表是交叉熵损失（Cross Entropy）

（1）均方误差损失（MSE）

均方误差损失（MSE）：均方误差适用于回归问题，计算的是预测值和真实值之间的欧氏距离，预测值和真实值之间越接近，均方误差就越小。MSE公式如下

$$MSE=\frac{1}{N}(\stackrel{︿}{y}-y{)}^2$$

• $N$：样本个数
• $\stackrel{︿}{y}$：样本真实值
• $y$：样本预测值

MSE在Pytorch中有实现，用法如下

loss_fn = torch.nn.MSELoss(reduction='sum')
loss = loss_fn(pred, y) / pred.size(0)

其实现如下

import torch.nn as nn
import torch
import random
#MSE损失参数
# loss_fun=nn.MSELoss(size_average=None, reduce=None, reduction='mean')
input=torch.randn(10)#定义输出(随机的1，10的数组）可以理解为概率分布
#tensor([-0.0712,  1.9697,  1.4352, -1.3250, -1.1089, -0.5237,  0.2443, -0.8244,0.2344,  2.0047])
print(input)
target= torch.zeros(10)#定义标签
target[random.randrange(10)]=1#one-hot编码
#tensor([0., 0., 0., 0., 0., 0., 0., 1., 0., 0.])
print(target)
loss_fun= nn.MSELoss()
output = loss_fun(input, target)#输出，标签
print(output)#loss:tensor(0.8843)
 
#=============不用nn.MSELoss实现均方差===================
result=(input-target)**2
result =sum(result)/len(result)#求和之后求平均
print(result)#tensor(0.8843)
#其结果和上面一样

（2）交叉熵损失（Cross Entropy）

• 交叉熵属于信息论中的内容，想要了解什么是交叉熵，必须先要了解信息量、信息熵和相对熵（KL 散度）等概念，一一介绍如下

信息量： 信息奠基人Shannon认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度

• “太阳从东边升起”：这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0
• 2026年中国队成功进入世界杯：首先，因为中国队进入世界杯的不确定性因素很大，而这句话消除了进入世界杯的不确定性，所以这句话的信息量非常大

所以，信息量的大小与信息发生的概率成反比，概率越大，信息量越小。概率越小，信息量越大。故设某一事件发生的概率为$P(X)$，则其信息量可表示为$I(X)=-log(P(x))$

---

信息熵： 用于表示所有信息量的期望，所以信息熵可以表示为$H(X)=-\sum _{i=1}^{n}P(x_i)log(P(x_i))$，$X=x1,x_2,...,x_n$

---

相对熵（KL散度）： 如果对于同一个随机变量$X$有两个单独的概率分布$P(X)$和$Q(X)$，则我们可以使用相对熵来衡量这两个概率分布之间的差异，即$D_{KL}(p||q)=\sum _{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i})$

在机器学习、深度学习中，常常使用$P(X)$和$Q(X)$分别代表样本的真实分布和模型的预测分布，例如对于一个三分类任务，一张图片的真实分布为$P(X)=[1,0,0]$，预测分布为$Q(X)=[0.7,0.2,0.1]$，则KL散度计算为0.36.所以KL散度越小表示$P(X)$与$Q(X)$的分布更加接近，因此可以反复训练$Q(X)$来使得$Q(x)$分布逼近$P(X)$

---

交叉熵： 将KL散度公式拆开后可发现，交叉熵=KL散度+信息熵

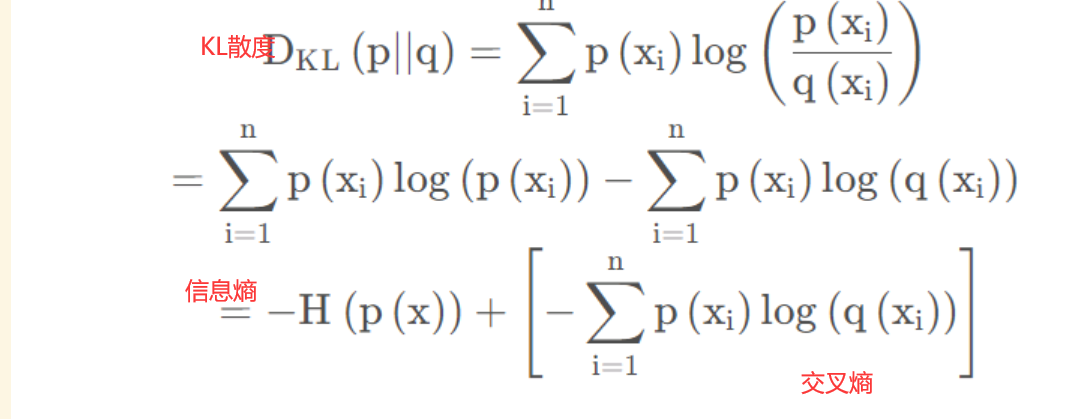
故$H(p,q)=-\sum _{i=1}^{n}p(x_i)log(q(x_i))$,在训练网络时，由于输入数据和标签常常已确定，所以真实概率分布$P(X)$就确定下来了，因此信息熵是一个常量，而交叉熵公式明显要比KL散度容易计算，所以我们直接最小化交叉熵来代替最小化KL散度作为损失函数

二：激活函数

激活函数：可以将非线性特性引入神经网络中。如下图神经元中，输入的inputs通过加权求和后还被作用了一个函数，这个函数就是激活函数

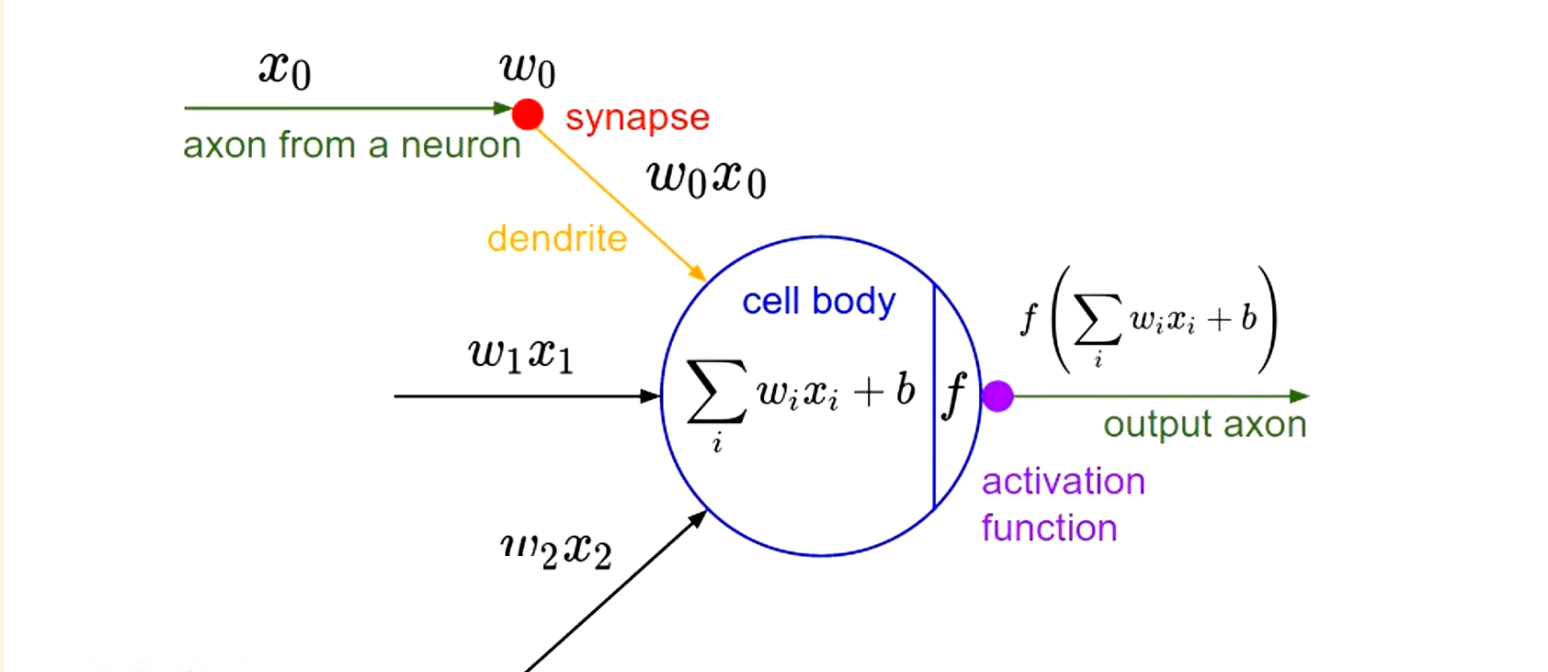
为什么需要激活函数？如果不使用激活函数，那么每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这样做就没有意义了。

• 没有激活函数：每一层都相当于是一个矩阵相乘，那么即便你叠加了n多层，无非还是矩阵相乘罢了

使用激活函数后，就会给神经元引入非线性因素，这使得神经网络可以任意逼近任何非线性函数（通用近似定理），这样神经网络就可以应用到众多非线性模型中

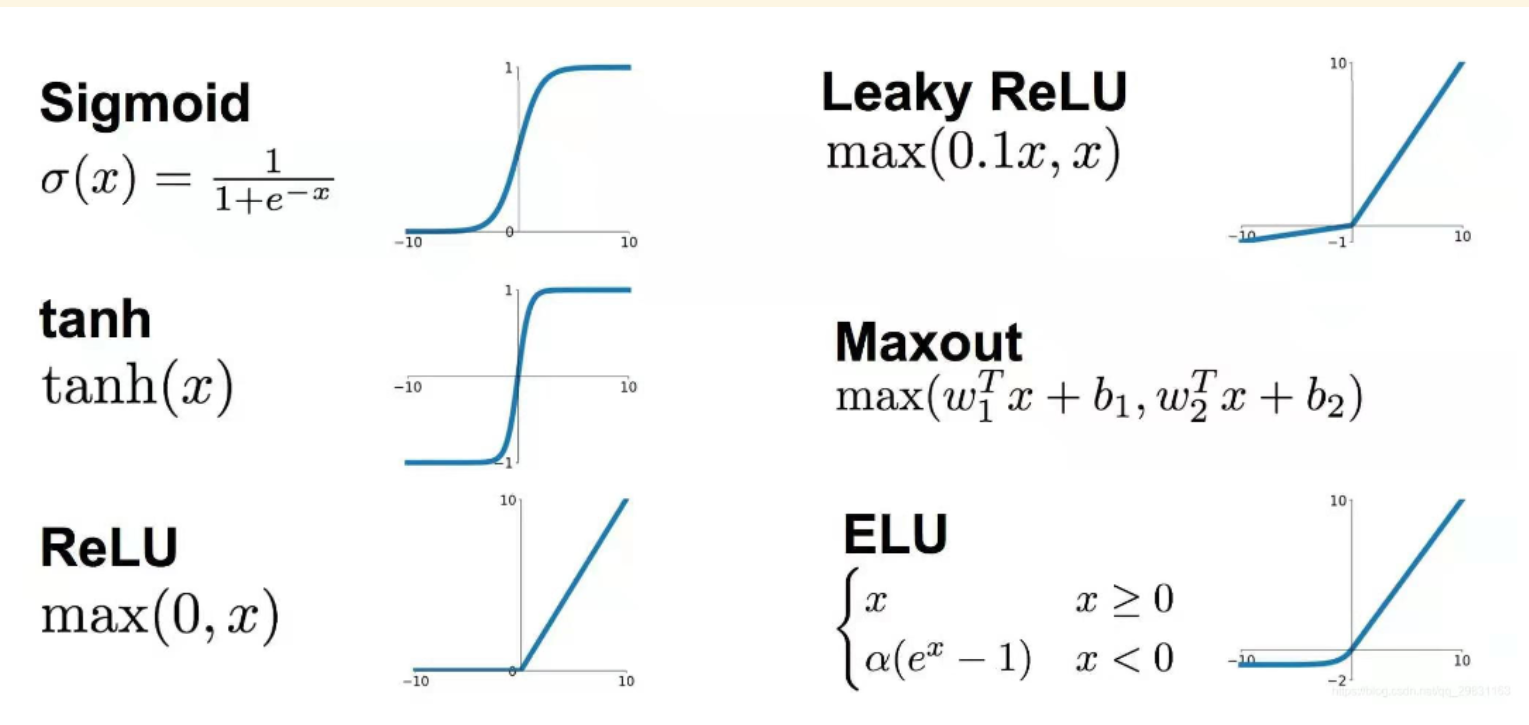
常用激活函数介绍如下，可分为如下两类

• 饱和激活函数：sigmoid、tanh

  • 非饱和激活函数相对于饱和激活函数来讲可以解决梯度消失问题，而且它能加快收敛速度

• 非饱和激活函数：ReLU、Leaky ReLU、ELU、PReLU、RReLU等

这里只介绍一下比较有名和重要的激活函数，如果需要了解其他激活函数可跳转至下面这篇文章

• 机器学习中的数学——激活函数：基础知识

（1）tanh

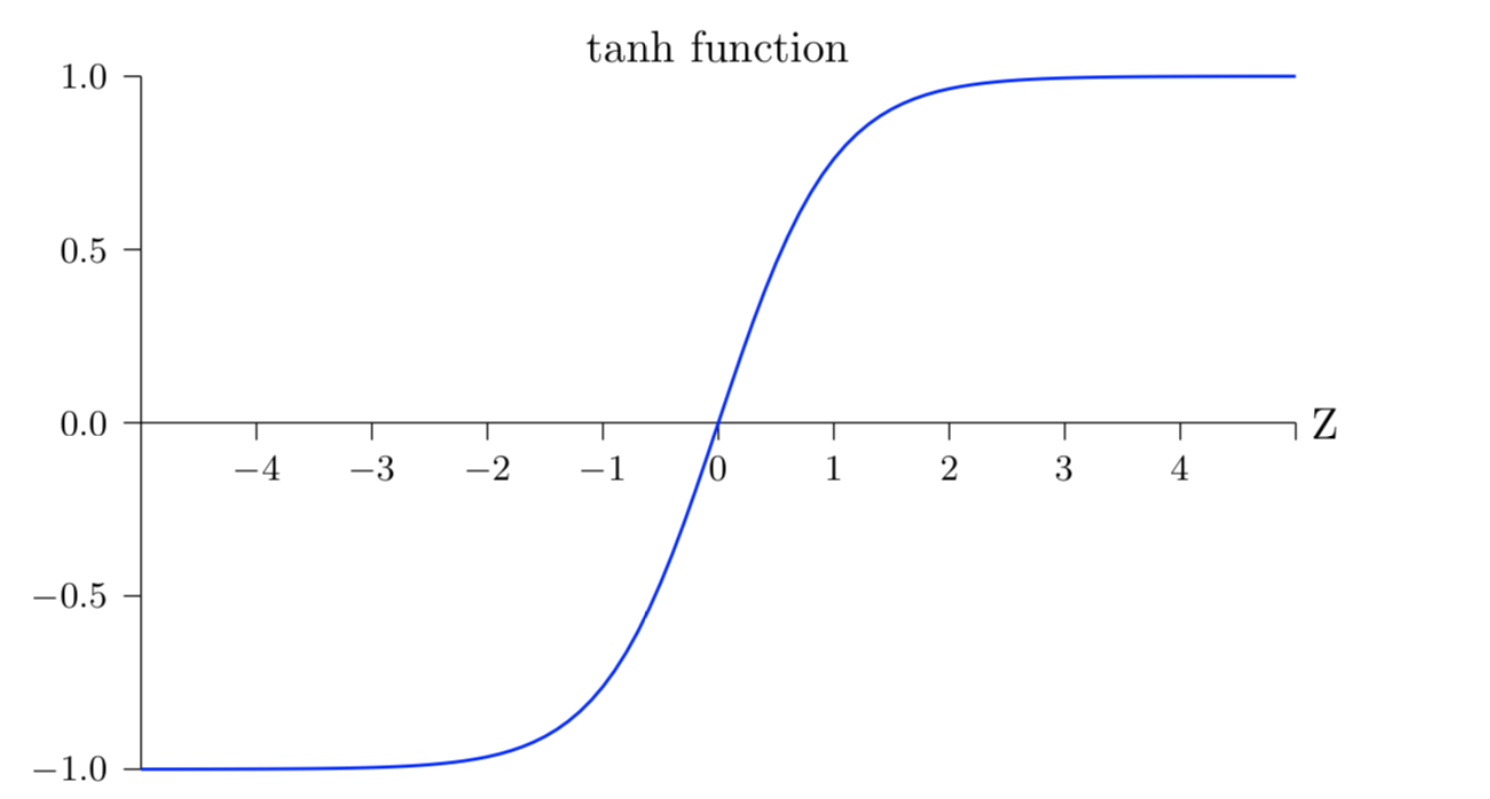
tanh：也即双曲正切函数，等于双曲余弦除以双曲正弦，它是一个奇函数。它相较于sigmoid函数提高了其收敛速度，但是仍然会导致梯度消失和梯度爆炸问题

$$tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

（2）ReLU

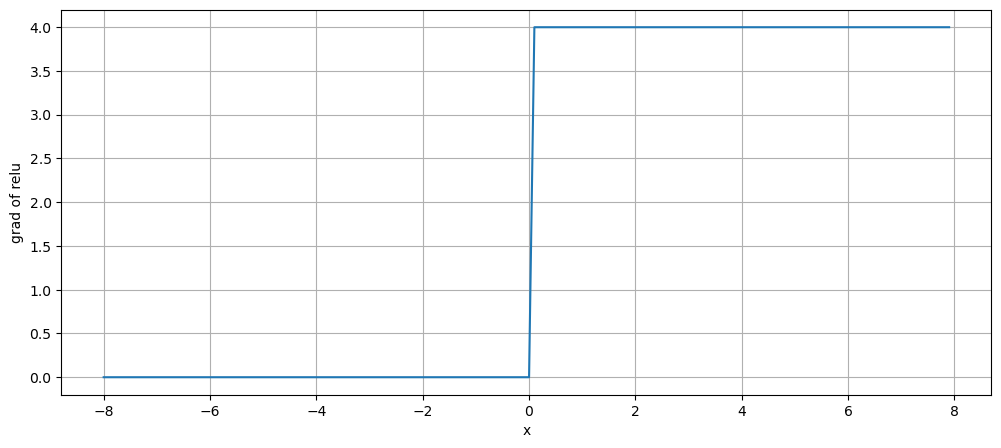
ReLU：也即修正线性单元，这是目前深度学习中最为常用的激活函数，是一种“万金油”式的激活函数。如下图，ReLU提供了一种非常简单的非线性变换，给定元素$x$，ReLU函数被定义为该元素与0的最大值

$$ReLU(x)=max(x,0)$$

ReLU函数通过将相应的活性值设为0，仅保留正元素并且丢弃所有负元素

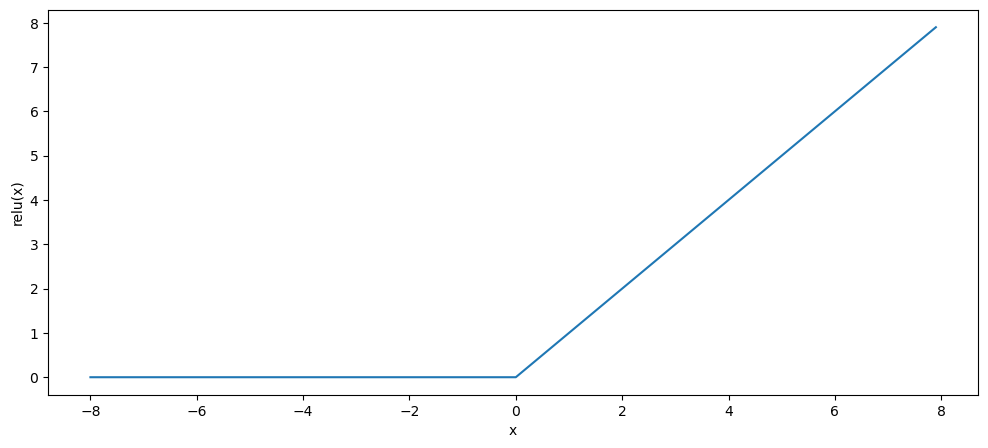
ReLU函数优点在于：其求导表现很好，要么让参数消失，要么让参数通过，所以在使用梯度下降法时收敛速度更快

（3）Leaky ReLU

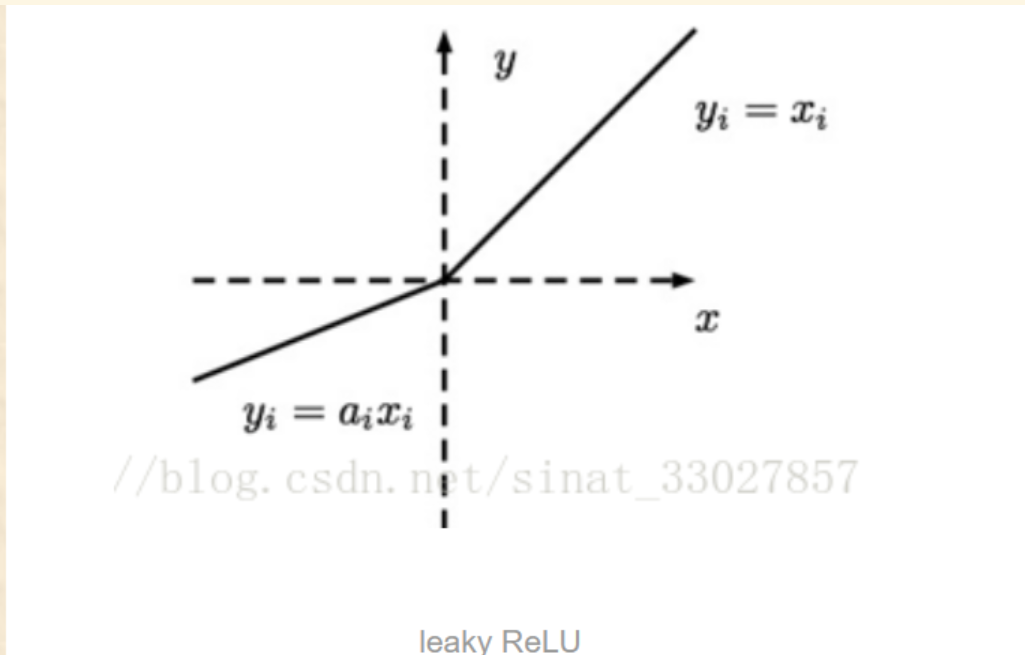
Leaky ReLU：与ReLU相比，Leaky ReLU给所有负值赋予一个非零斜率，leaky是一个很小的数$a_i$，这样就保留了一些负轴的值，使得负轴的信息不回全部丢失

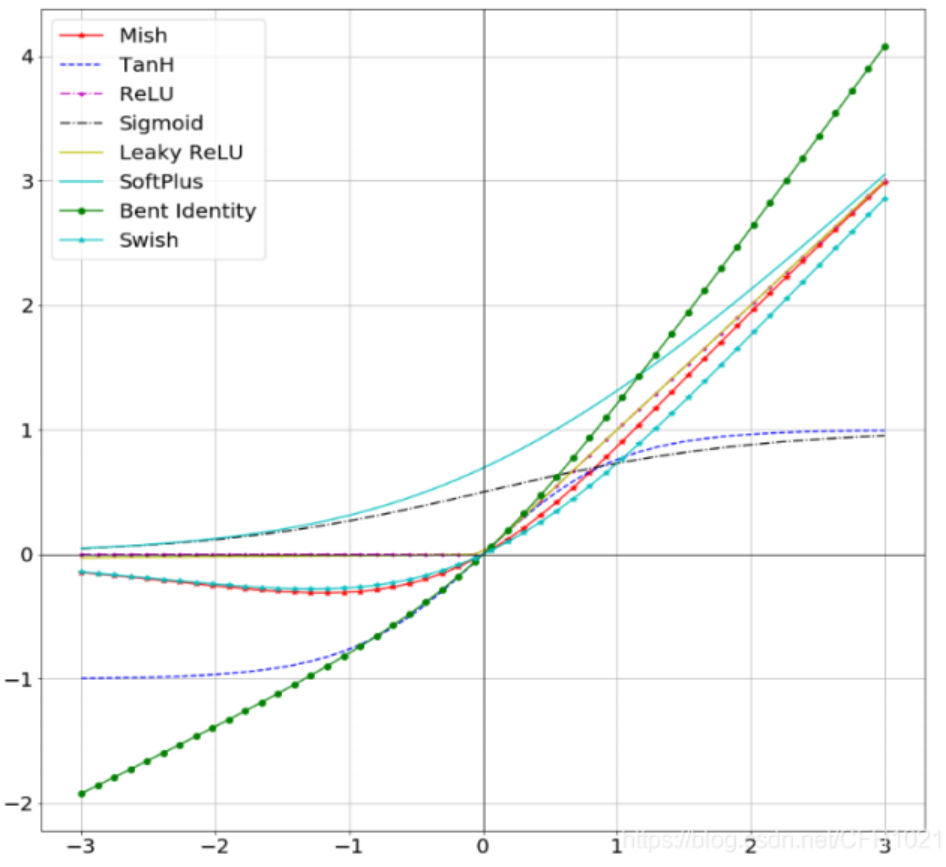
（4）mish

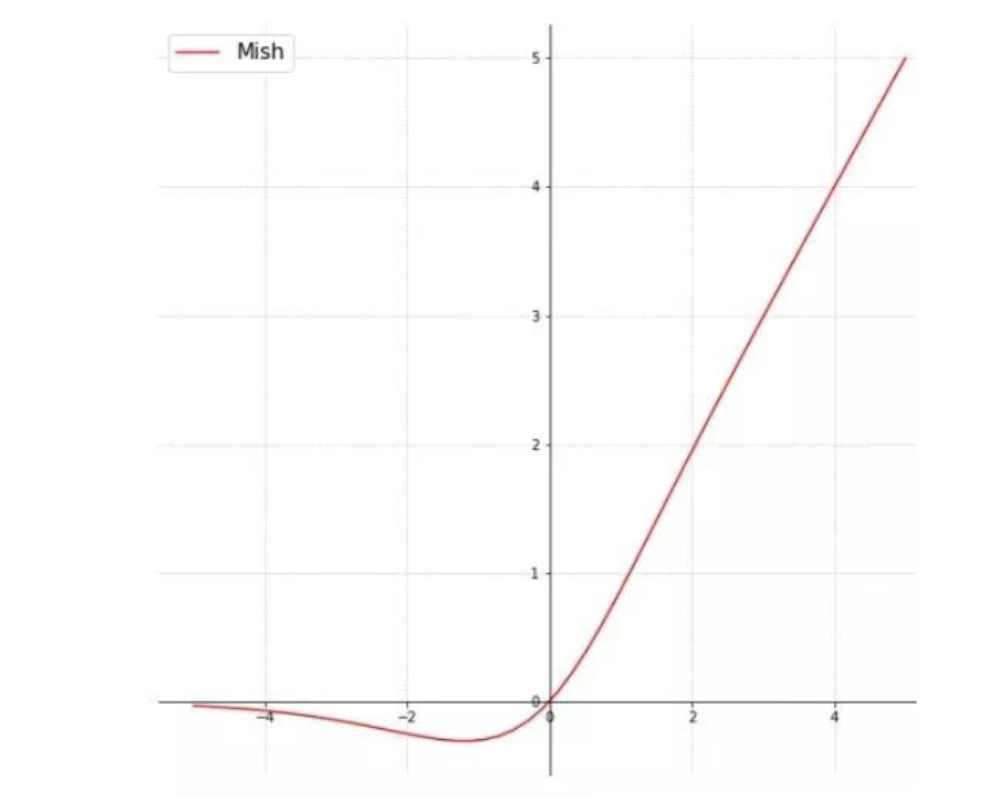
mish：这是20左右新提出来的一个激活函数，经验证，该函数精确度要比ReLU高1.671%，所以很多时候我们也会选择它作为激活函数，其公式为

$$mish(x)=x\ast tanh(softplus(x))$$

• $softplus(x)=\frac{1}{\beta }\ast log(1+e^{\beta x})$：Softplus可以看作是Relu平滑版本

Mish激活函数无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许更好的梯度流，而不是像ReLU中那样的硬零边界、同时，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化

Pytorch中的写法

import torch
import torch.nn.functional as AF
import warnings
warnings.filterwarnings("ignore")

# 定义一个线性层
layer = torch.nn.Linear(in_features=16, out_features=5)
X = torch.randn(size=(8, 16))
pred = layer(X)
print(pred.size())

###   激活函数不会改变输入数据维度   ###

# sigmoid激活函数
sigmoid = AF.sigmoid(pred)
print(pred.size())

# ReLU激活函数
ReLU = AF.relu(pred)
print(pred.size())

# leaky ReLU激活函数
leay_ReLU = AF.leaky_relu(pred)
print(pred.size())

# mish激活函数
leay_ReLU = AF.mish(pred)
print(pred.size())