前缀和
用来求解一段区间(一维)的总和
或者一块矩形区域(二维)的总和
一维前缀和
原数组a[N],前缀和数组s[N]
// ---
读入数组a[N]
// ---
// 处理前缀和数组 s[N]
s[0] = 0; //定义在全局变量,不用写这一句
for (int i = 1; i <=n; i++)
s[i]=s[i-1]+a[i];
//-求解答案
区间[L, R]的和:ans=s[r]-s[l-1]
二维前缀和
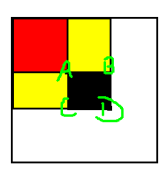
如图,需要求黑色矩形的总和,就需要用到二维前缀和。
二维前缀和的s[N][N]代表从(0,0)点到(x,y)点的矩形区域的总和,例如红色区域S[A]。
求解黑色区域:S[D] - S[A] = S[D点] - 上部分多的 - 左部分多的 + 多减去的部分A
求解全部区域:S[全部] = 上部分的 + 左部分的 - 多加的部分A + a[D点]
原数组a[N][N],前缀和数组s[N][N]
// ---
读入矩阵数组a[N][N]
// ---
// 处理前缀和数组 s[N][N]
for (int i = 1; i <=n; i++)
for (int j = 1; j <=n; j++)
s[i][j] = s[i−1][j] + s[i][j−1] − s[i−1][j−1] + a[i][j]
//-求解答案
一块矩形区域的和(上图黑色区域):ans = s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
差分
差分可以简单的看成序列中每个元素与其前一个元素的差。
原数组a[N] 进行差分,得到差分数组b[N] ,差分数组求前缀和,又得到原数组a[N]
差分数组改变–再求前缀和,得到改变后的数组(一段区间加上一个常数C)
5,6, 4,8, 7, 6,9
5 1 -2 4 -1 -1 3
一维差分
一个区间[L,R]中的每一个数全部加上一个C或者减去一个C
// 编写差分函数,生成差分数组和进行差分操作都是用这一个函数即可
// 区间[l,r]中的所有值都加上常数c
void insert(int l, int r, int c){
b[l] += c;
b[r+1] -= c;
}
// 只在l位置加了C,前面的[1, l-1]前缀和加回去,还是原数,没变。
// 从l往后都会多加一个c,
// 但是只需要l---r这个区间加C,r之后的[r+1, .....],不能加 要保持不变,
// 但是多加了C,需要减去C,也就是让[r+1, .....]这些,每次都需要-C,这样+-就平衡了
// 对应到差分数组就是在b[r+1]的地方 -C
// 通过上面就看出来了,对差分数组i位置进行 +- 操作,对应的包括i位置以及之后的,都是进行 +-C 的操作,会一直往后影响(对原数组)。
// 对于二维差分,一样的思路

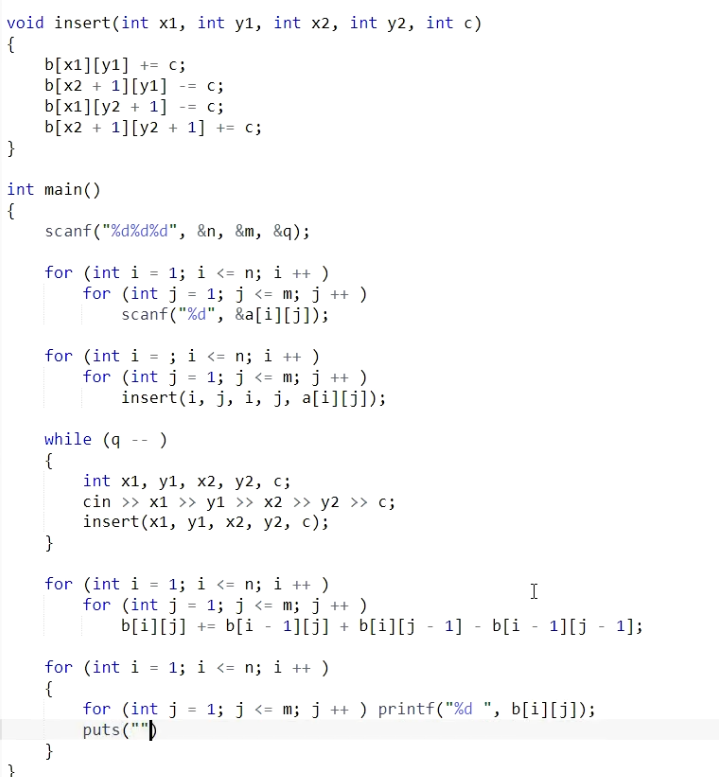
二维差分
给一个子矩阵的所有数都加上一个数C
void insert(int x1, int y1, int x2, int y2, int c){
b[x1][y1] += c;
b[x2+1][y1] -=c;
b[x1][y2+1] -=c;
b[x2+1][y2+1] += c;
}