；例题引入：
在跳楼梯问题中，我们假设每次可以跳1级或2级。如果我们想跳到第N级台阶，那么我们的最后一次跳跃只能是1级或2级。
如果我们最后一次跳1级，那么我们必须先跳到第N-1级台阶。由于跳到第N-1级台阶有f(N-1)种方法，因此通过这种方式跳到第N级台阶的方法数也是f(N-1)。
如果我们最后一次跳2级，那么我们必须先跳到第N-2级台阶。类似地，由于跳到第N-2级台阶有f(N-2)种方法，因此通过这种方式跳到第N级台阶的方法数也是f(N-2)。
因此，跳到第N级台阶的总方法数就是这两种方式的方法数之和，即f(N) = f(N-1) + f(N-2)。这正是斐波那契数列的定义。
这个逻辑基于的是这样一个事实：任何到达第N级台阶的路径都可以通过最后一次跳1级或2级从更低级别的台阶到达。由于这两种跳跃方式是互斥的（即最后一次跳跃不能同时是1级和2级），因此我们可以将问题分解为两个子问题，并将它们的解决方案相加来得到原问题的解决方案。
#include<iostream>
using namespace std;
int n;
int fib(int x)
{
if(x==1)
return 1;
if(x==2)
return 2;
return fib(x-1)+fib(x-2);}
int main(){
scanf("%d",&n);
int res=fib(n);
printf("%d\n",res);
return 0;}注意：scanf与cin
n>10^5时，cin和cout比scanf,printf慢一倍或更多，建议直接用scanf和printf
递归的层数太多会导致时间复杂度过大
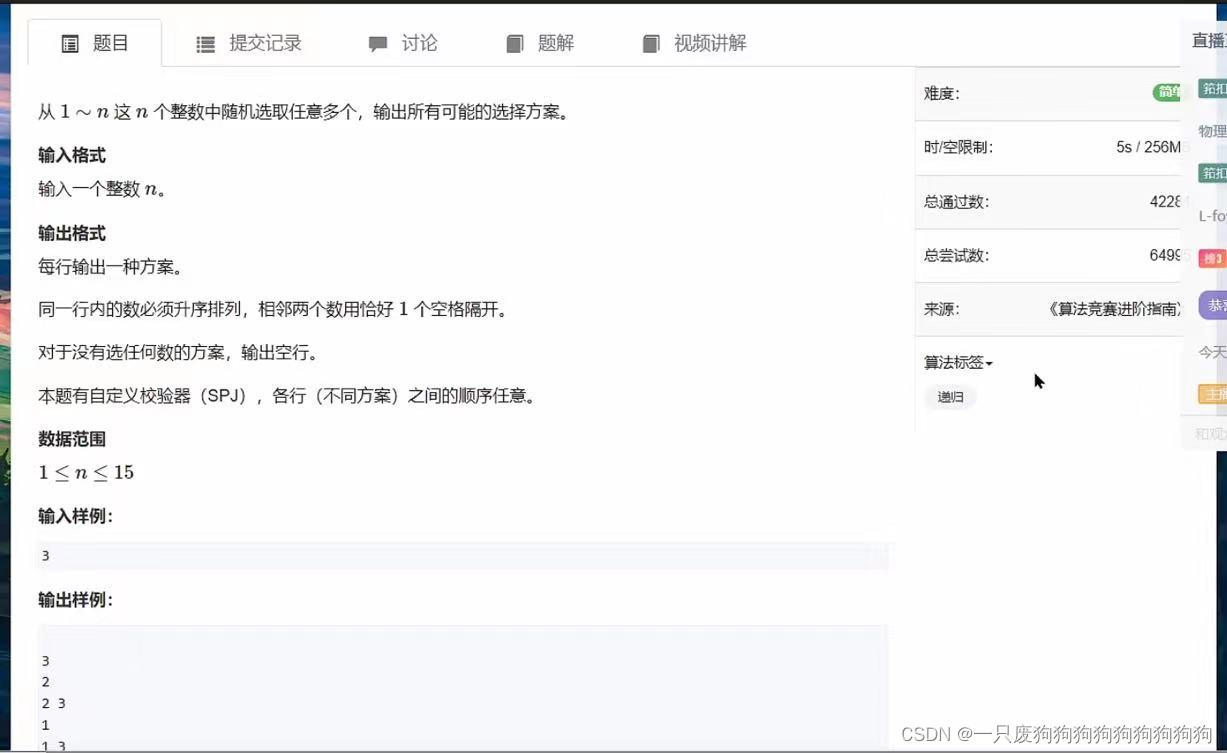分析：每一个数字都有两个选择：选或者不选，所以n个数字一共有2^n中情况
DFS的主要思想是，深度优先
思路：用一个长度为n的数组记录选还是不选
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 20;//构建数组使用
int n;
int st[N];//记录每个数字的状态，0表示暂未考虑，1表示已选，2表示不选这个数
int dfs(int x)
{
if (x > n)//超出原本范围，跳出分枝打印数字,打印的是最深层的所有情况，例n=3,则打印8种情况
{
for (int i = 1; i <= n; i++)
{
if (st[i] == 1)//被选中
{
printf("%d ", i);
}
}
printf("\n");
return 0;
}
//选择该数字的情况
st[x] = 1;
dfs(x + 1);//确定下一个数字
st[x] = 0;//程序回溯，用0表示初始状态
//不选择该数字的情况
st[x] = 2;
dfs(x + 1);
st[x] = 0;
}
int main()
{
cin >> n;
dfs(1);
system("pause");
return 0;
}全排列问题：
字典序：
例：strcmp字符比较函数，“abc"与”abd",依次按序比较ascii码，abc<abd
思路：1，依次枚举每个位置应该放哪个数。2，依次枚举每个数应该放哪个位置
方法1：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 20;//构建数组使用
int n;
bool st[N];//布尔类型记录是否被选择
int arr[N];//记录数组
int dfs(int x)//当前枚举到的数字
{
if (x > n)//超出原本范围，跳出分枝打印数字,打印的是最深层的所有情况，例n=3,则打印8种情况
{
for (int i = 1; i <= n; i++)
{
printf("%5d ", arr[i]);//打印当前结果，保留5个场宽
}
printf("\n");
return 0;
}
for (int i = 1; i <= n; i++)//遍历
{
if (!st[i])//没被选过,用bool类型可以保证每次选择的数字不与已选数字重复
{
st[i] = true;
arr[x] = i;
dfs(x + 1);//下一个位置
st[i] = false;//完成后，回溯需要初始化
arr[x] = 0;
}
}
}
int main()
{
cin >> n;
dfs(1);
system("pause");
return 0;
}
组合练习：
分析：组合不讲究顺序，例 ：1，2，3只有一个组合：1和2和3没有顺序
但在本题中，后一个数字比前一个数字要大，则为123
思路：1，依次枚举每个位置应该放哪个数。2，依次枚举每个数应该放哪个位置
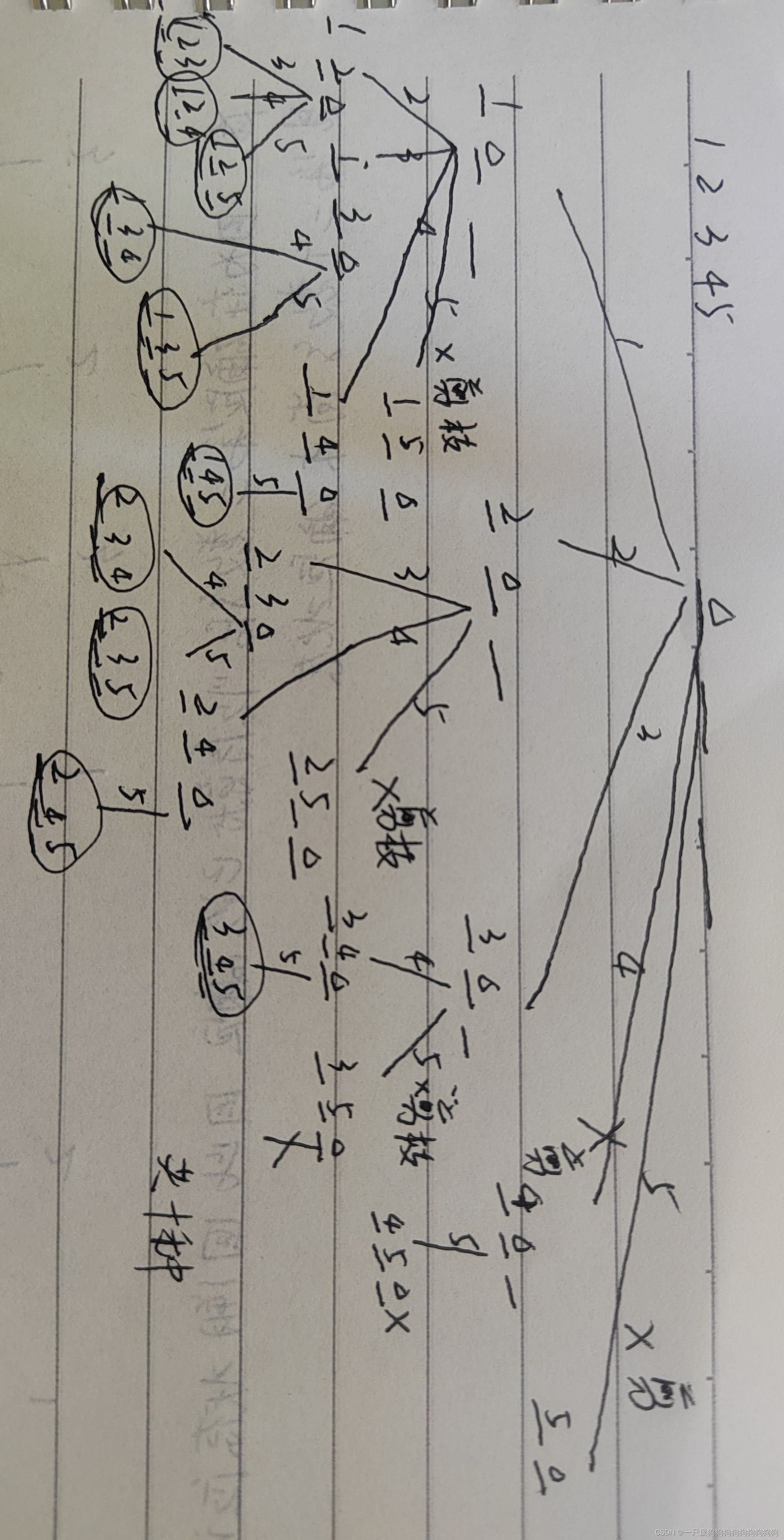
以方法2为例：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 20;//构建数组使用
int n;
int r;
int arr[N];//记录选了哪些数字
int dfs(int x,int start)//记录当前枚举到的位置
{
if (x > r)//超出原本范围
{
for (int i = 1; i <= r; i++)
{
printf("%3d ", arr[i]);//打印当前结果
}
printf("\n");
return 0;
}
for (int i = start; i <= n; i++)//保证后面的数递增
{
arr[x] = i;
dfs(x + 1,i+1);//下一个位置
arr[x] = 0;
}
}
int main()
{
cin >> n>>r;
dfs(1,1);//第一个位置从1开始枚举
system("pause");
return 0;
}
选数
分析：
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 30;//构建数组使用
int n;
int k;
int arr[N];//记录选了哪些数字
int res = 0;
int a[N];//存储原始数据
bool isprime(int sum)
{
if (sum < 2)return false;
for (int i = 2; i <= sum / i; i++)//判断条件i*i<sum,但是当i数值非常大时有可能超出int范围
{
if (sum % i == 0)
return false;
}
return true;//不能放在内部判断
}
int dfs(int x, int start)//记录当前枚举到的位置
{
int sum = 0;
if (x > k)//超出范围，打印结果
{
for (int i = 1; i <= k; i++)
{
sum += arr[i];
}
if (isprime(sum))
{
res++;
}
return 0;
}
for (int i = start; i <= n; i++)
{
arr[i] = a[i];
dfs(x + 1,i+1);//下一个数字对应下一个数字
arr[i] = 0;
}
}
int main()
{
cin >> n>>k;
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
dfs(1,1);//第一个位置从1开始枚举
printf("%d", res);
system("pause");
return 0;
}
剪枝思想：
当已有数字和可选择数字一共的数量<k，则需要剪枝
例：有1，2，3，4，5.第一个空为4，可选择的只有5 ，数量为2<3,则需要剪枝
代码表示：
if((x-1)+n-start+1)<k){return;}
剪枝后可以缩短运行时间
