编辑切换为居中
添加图片注释,不超过 140 字(可选)
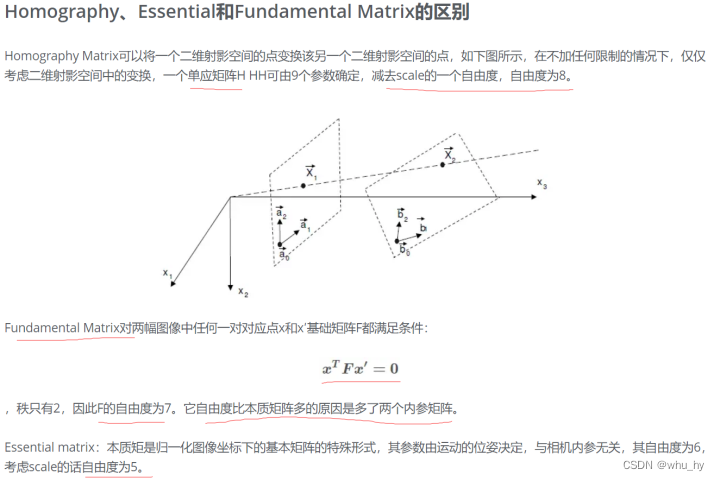
三个矩阵的自由度:
单应矩阵H 自由度8
基础矩阵F 自由度7
本质矩阵E 自由度5或者8,这个是根据使用旋转矩阵还是旋转向量

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
旋转矩阵是3个自由度,那么本质矩阵自由度应该是5。完了,我方了。。。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
在这里的x1和x2是在推导过程中用来替代的变量,知道它的表达形式,但是具体啥含义还是不太清楚。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
E不涉及内参,那么它只与外参相关。而F与内参和外参都相关。

编辑
添加图片注释,不超过 140 字(可选)
F的秩为2,根据F的表达式,同时有可逆矩阵不改变矩阵的秩,那么F的秩和tx的秩相等,同时tx的秩为2,所以F的秩为2即证。
编辑
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
简单来说单应矩阵描述的是平面与平面之间的关系。用途广泛,可以用来进行视角转换以及ARVR这些应用。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面是单应矩阵和对极约束的总结。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这幅图说明对极约束的意义,这个对极约束反映了点到直线之间的映射关系,并不是点到点的对应关系,因此P1不能准确地对应到P2上面,但是我们可以通过对极约束知道P2肯定在极线l2上面。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
和上面那幅图一个意思,就说左边的P对应到右边平面上,然后对应点肯定落在l’这条极线上面,具体是哪个点的话是不清楚的,但是这样也算是大大减少了计算量。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
旋转矩阵具有3个自由度。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
n维旋转矩阵的自由度如上所示,n(n-1)/2