算法竞赛基础：树状数组

是什么？

树状数组虽然语义上是树状，但是实际上还是一个数组。

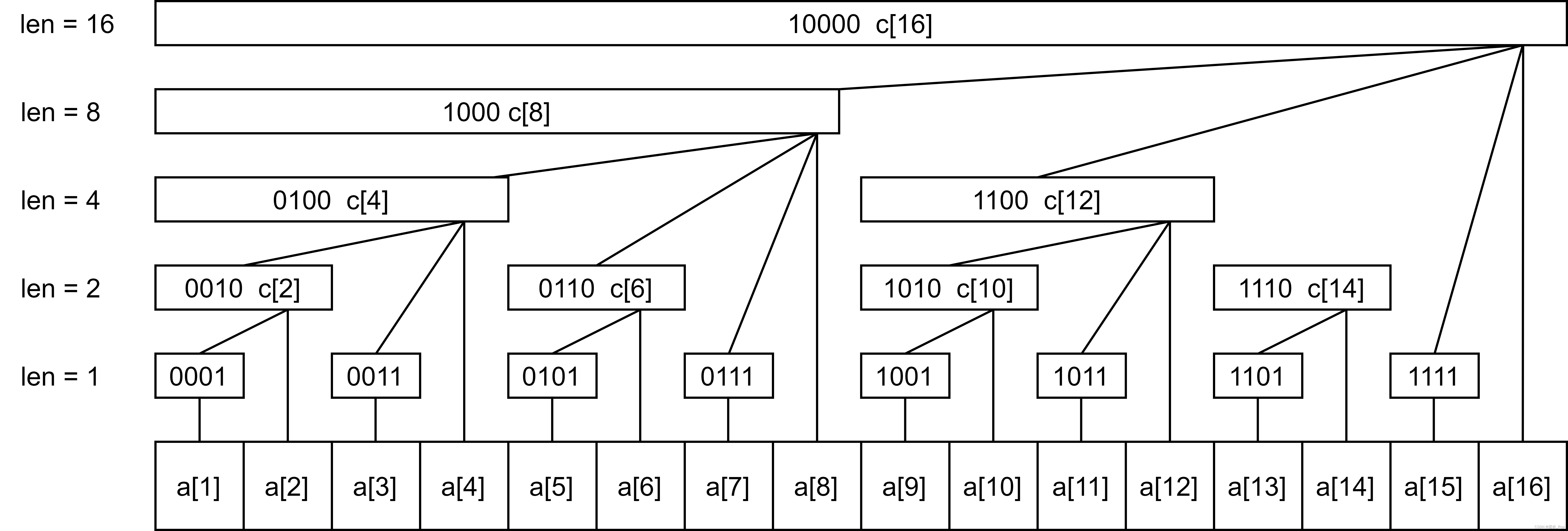
树状数组的功能就是单点和区间的修改和查询。
例如，如果想增加一个点的值，那么你需要让其上方所有能对齐的树状数组c全部增加相同的值，在查询包含该数组的区间时，从区间最右端端点处可以访问，将所有小于c[i]且len大于等于c[i]`的数组数组相加，就是要查询的值。

例如，当我们在a[6]上增加2的时候，向上对齐的数组c[6],c[8],c[16]同样增加2

如果我们想要查询1到7的区间，则需要从最右端开始，也就是c[7](图中未标出，为0111的位置)，加上c[6]，c[4] 所得值就是结果。

为什么？

如果向右和向左访问呢？树状数组利用的是二进制的性质，如果我们想访问i + 1，那么我们应该让 i += lowbit(i)，其中lowbit(i)是关于i的一个位运算：

lowbit(i) = i & -i

这样做会只留下i的二进制最右边的1，例如：
i = 00110110，经过这样的运算之后，i会变成：00000010

同理，向左访问树状数组时，通常让i -= lowbit(i)

怎么做？

这里列出树状数组的单点修改和求和模板代码：

// lowbit函数需要自己写
int lowbit(int x) {
	return x & -x;
}

// 单点修改
void update(ll k, ll x) {
	for (int i = k; i <= n; i += lowbit(i)) t[i] += x;
	return ;
}

// 求和
void getsum(int k) {
	int ans = 0;
	for (int i = k; i > 0; i -= lowbit(i)) ans += t[i];
	return ans;
}

模板题

样例输入：

5 4
1 2 3 4 5
1 1 1
2 1 2
1 4 2
2 3 4

样例输出：

4
9

题解代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAX_N = 2e5 + 100;

// t是树状数组
ll a[MAX_N], t[MAX_N];
int n, q;

int lowbit(int x) {
	return x & -x;
}

void update(int k, ll x) {
	for (int i = k; i <= n; i += lowbit(i)) t[i] += x;
	return ;
}

ll getsum(int k) {
	ll res  = 0;
	for(int i = k; i > 0; i -= lowbit(i)) res += t[i];
	return res;
}

void solve() {
	cin >> n >> q;
	// 读入数据，并且时刻更新树状数组
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) update(i, a[i]);
	
	// 读状态
	while (q--) {
		int op; cin >> op;
		if (op == 1) {
			// 单点修改
			ll k, v; cin >> k >> v;
			update(k, v);
		} else {
			// 区间查询
			ll l, r; cin >> l >> r;
			cout << getsum(r) - getsum(l - 1) << '\n';
		}
	}
	return ;
}

int main() {
	solve();
	return 0;
}