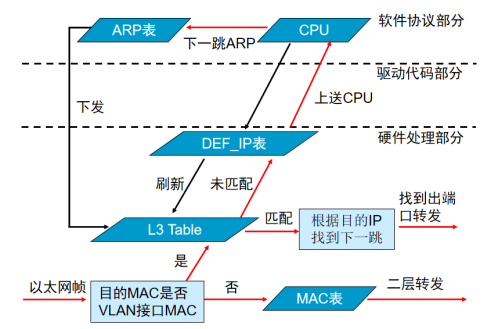
sigmoid
公式: s i g m o i d ( x ) = 1 1 + e − x sigmoid(x) = \frac{1}{1 + e^{-x}} sigmoid(x)=1+e−x1
函数曲线如下:
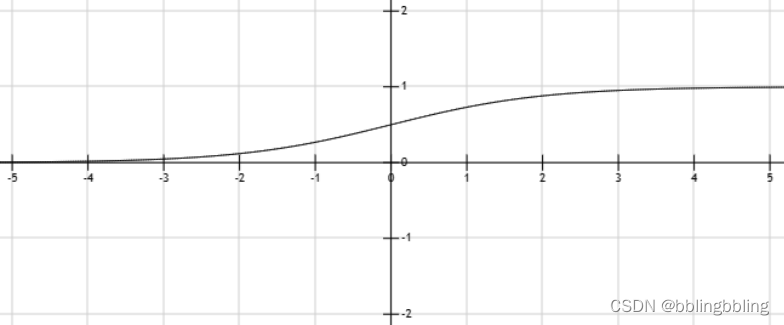
导数公式: f ( x ) ′ = e − x ( 1 + e − x ) 2 = f ( x ) ( 1 − f ( x ) ) f(x)\prime = \frac{ e^{-x}}{(1 + e^{-x})^2} = f(x)(1-f(x)) f(x)′=(1+e−x)2e−x=f(x)(1−f(x))
导数曲线如下:
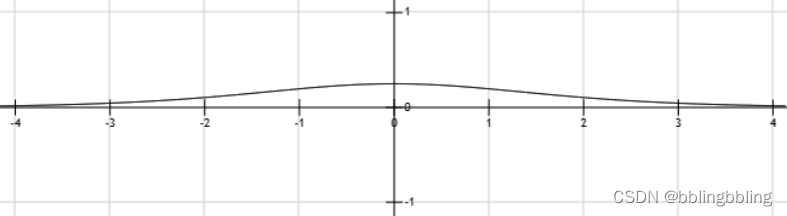
sigmoid代码:
import torch
import torch.nn.functional as F
// sigmoid函数
x = torch.tensor([1.0, 2.0, 3.0])
// y = 1 / (1 + torch.exp(-x))
y = torch.sigmoid(x)
print(f"sigmoid result: {y}")
print(f"sigmoid derivative: {y * (1 - y)}")
softmax
公式:
s
o
f
t
m
a
x
(
z
i
)
=
z
i
∑
j
=
1
n
e
z
j
softmax(z_i) = \frac{z_i}{\sum_{j=1}^n e^{z_j}}
softmax(zi)=∑j=1nezjzi
指数函数曲线:
y
=
e
x
y= e^{x}
y=ex
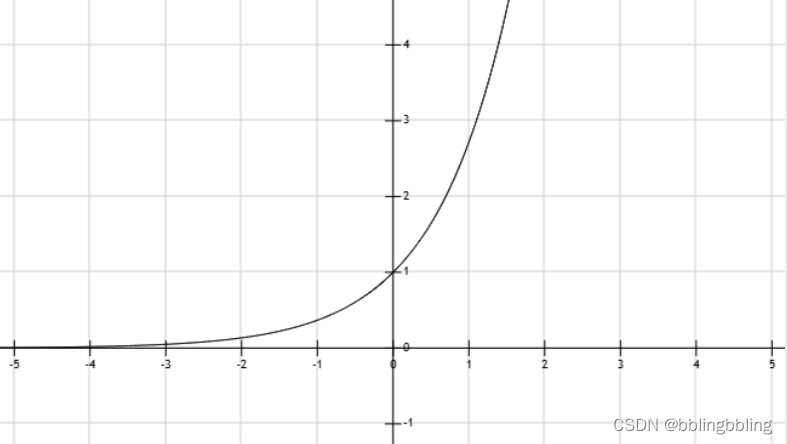
- 引入指数形式的优点:
指数函数曲线呈现递增趋势,斜率逐渐增大,在 x 轴上一个很小的变化可以导致 y 轴上很大的变化。 - 引入指数形式的缺点:
当 z值非常大时,计算得到的数值会变得非常大,可能会溢出。通常针对数值溢出的方法,是将每一个输出值减去输出值中的最大值。
导数公式:
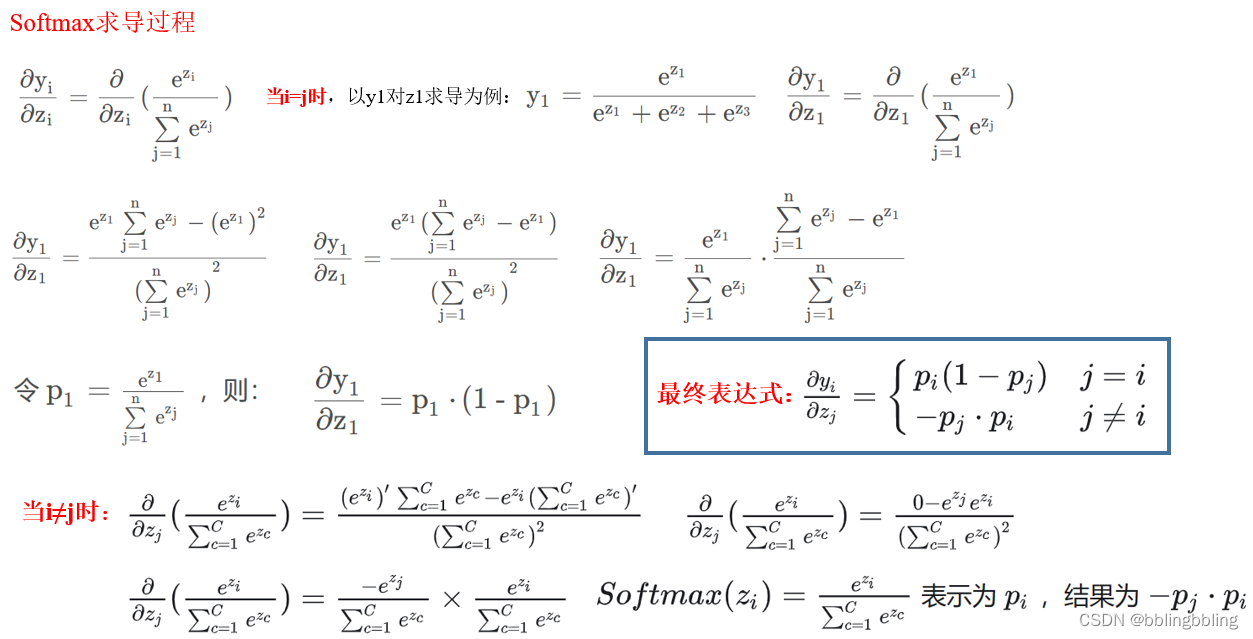
softmax代码:
import torch
import torch.nn.functional as F
def softmax(x):
"""Compute the softmax of vector x."""
exps = np.exp(x)
return exps / np.sum(exps)
// softmax函数
x = torch.tensor([1.0, 2.0, 3.0])
y = F.softmax(x, dim=0)
print(f"softmax result: {y}")
print(f"softmax derivative: {torch.diag(y) - torch.outer(y, y)}")
softmax与cross entropy的联系
事实上,交叉熵与Softmax没有直接的关系。
交叉熵本质是衡量两个概率分布的距离的,而softmax能把一切转换成概率分布。
H
(
L
,
P
)
=
−
∑
j
=
1
n
L
j
l
o
g
(
P
j
)
H(L,P) = -\sum_{j=1}^nL_jlog(P_j)
H(L,P)=−j=1∑nLjlog(Pj)
其中P是预测概率分布,L是真实标签分布。











![[Redis]——数据一致性,先操作数据库,还是先更新缓存?](https://img-blog.csdnimg.cn/direct/3e043ea768e0470db53c0bfd3d15162e.png)