1. stack的介绍和使用
1.1 stack的介绍
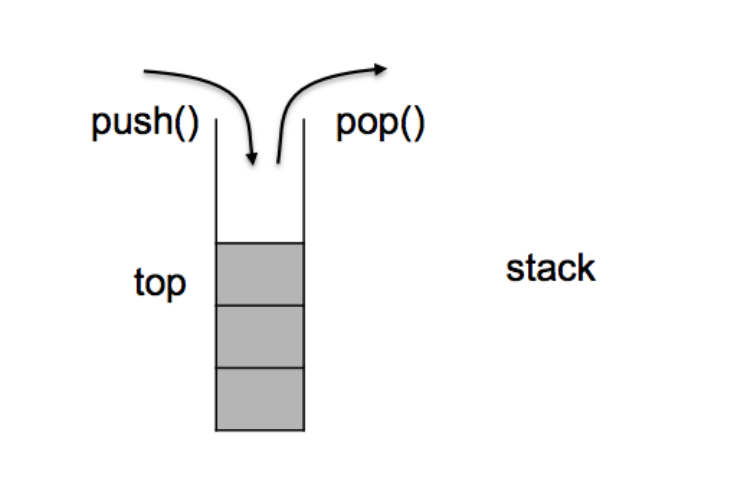
1. stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行
元素的插入与提取操作。
2. stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容器,并提供一组特定
的成员函数来访问其元素,将特定类作为其底层的,元素特定容器的尾部(即栈顶)被压入和弹出。
3. stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类,这些容器类应该支持以下
操作:
empty:判空操作
back:获取尾部元素操作
push_back:尾部插入元素操作
pop_back:尾部删除元素操作
4. 标准容器vector、deque、list均符合这些需求,默认情况下,如果没有为stack指定特定的底层容器,
默认情况下使用deque。
1.2 stack的使用
函数说明 | 接口说明 |
stack() | 构造空的栈 |
empty() | 检测stack是否为空 |
size() | 返回stack中元素的个数 |
top() | 返回栈顶元素的引用 |
push() | 将元素val压入stack中 |
pop() | 将stack中尾部的元素弹出 |
1.3 stack的oj练习
最小栈
思路:我们可以利用一个 辅助栈去记录一下每次插入数据之后的最小值,如图:

代码实现 :
class MinStack {
public:
MinStack() {
//这里的构造函数可以不写,因为自定义类型会默认生成
}
void push(int val) {
data_st.push(val);
//最小栈只有val小于等于栈顶元素的时候和min_st为空才入栈
if(min_st.empty() || val <= min_st.top())
{
min_st.push(val);
}
}
void pop() {
//判定最小栈是否需要出栈
if(data_st.top() == min_st.top())
{
min_st.pop();
}
data_st.pop();
}
int top() {
return data_st.top();
}
int getMin() {
return min_st.top();
}
private:
stack<int> data_st;//数据栈
stack<int> min_st;//最小栈
};栈的弹出压入序列
思路:入栈序列不断入栈,当栈顶元素和出栈序列的元素相同时就出栈,到最后入栈栈中没有元素则说明这出栈序列是正确的,否则说明这个出栈序列是不符合栈的规则的。

代码实现:
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> result;
//如果result为空或者result的栈顶元素和popv中的不同就入栈
int i = 0;
for(auto e: pushV)
{
result.push(e);
//判断是否popV中的值是否和栈中的元素相同
while(!result.empty() && popV[i] == result.top())
{
result.pop();
i++;
}
}
return result.empty();
}
};逆波兰表达式求值
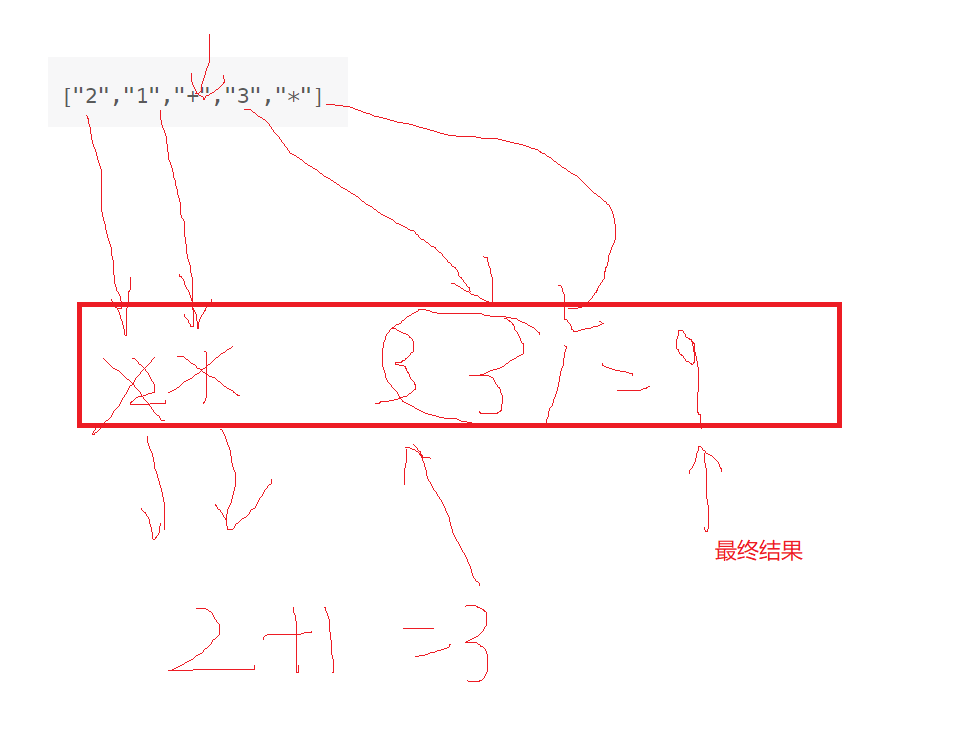
思路:首先我们要意识到为什么要这样求值,这样 为了让计算机更好的进行计算。这题我们可以把 数字字符先入栈,如果遇到非数字字符,我们就把栈顶的两个数字字符拿出来进行运算, 运算完成把结果放入栈中。其中我们要注意的是计算的左右操作数的问题,因为对于 -和/两个操作符是有左右要求的,所以我们需要记录一下。
代码实现:
class Solution {
private:
stack<int> st;
public:
int evalRPN(vector<string>& tokens) {
//两个数字一个操作符对应,是数字就入栈,遇到操作符就把栈顶的两个元素拿出来操作
//判断操作符
for(auto& e: tokens)
{
if(e == "+" || e == "-" || e == "*" || e == "/")
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
//进行操作,然后存放到栈中
switch(e[0])
{
case '+':
st.push(left + right);
break;
case '-':
st.push(left - right);
break;
case '*':
st.push(left * right);
break;
case '/':
st.push(left / right);
break;
}
}
else
{
//入栈
st.push(stoi(e));
}
}
return st.top();
}
};实现完这题之后,我们再来了解一下中缀表达式如何转换成后缀表达式的。

1.4 stack的模拟实现(了解设计模式)
我们先了解一下什么是设计模式:设计模式就是根据已有的优良的方案去设计出新的成品,解决想要解决的问题。这篇文章很详细的介绍了设计模式: https://blog.csdn.net/weixin_57504000/article/details/124195306
我们当时在使用C语言实现栈的时候,其实也是使用的数组来实现,那么在C++中我们一样不需要自己实现,我们可以采用适配器模式去设计即可。适配器模式也就是已经有的东西封装出你想要的东西。在我们之前其实也见过一种模式就是迭代器模式,就是不让使用者看到底层的细节,封装后使用统一的方式去使用。
下面我将使用适配器模式去模拟实现栈,过程非常简单:
#include <deque>
#include <vector>
namespace liang
{
//使用适配器模式设计
//这里也可以使用vector :template<class T, class Container = vector<T>>
template<class T, class Container = deque<T>>
class stack
{
public:
void push(const T& val)
{
_con.push_back(val);
}
T& top()
{
return _con.back();
}
const T& top() const
{
return _con.back();
}
void pop()
{
_con.pop_back();
}
size_t size()const
{
return _con.size();
}
bool empty()const
{
return _con.size() == 0;
}
private:
Container _con;
};
}这里的deque后面再介绍
2. queue的介绍和使用
2.1 queue的介绍
1. 队列是一种容器适配器,专门用于在FIFO上下文(先进先出)中操作,其中从容器一端插入元素,另一端
提取元素。
2. 队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的
成员函数来访问其元素。元素从队尾入队列,从队头出队列。
3. 底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操
作:
empty:检测队列是否为空
size:返回队列中有效元素的个数
front:返回队头元素的引用
back:返回队尾元素的引用
push_back:在队列尾部入队列
pop_front:在队列头部出队列
4. 标准容器类deque和list满足了这些要求。默认情况下,如果没有为queue实例化指定容器类,则使用标
准容器deque。

2.2 queue的使用

2.3 queue的模拟实现
队列的实现和栈的实现也是使用的适配器的设计模式:因为尾插头删的缘故,我们一般使用链表,但是这里使用deque来处理:
#include <deque>
namespace lra
{
template<class T,class container = deque<T>>
class queue
{
public:
void push(const T& val)
{
_con.push_back(val);
}
void pop()
{
_con.pop_front();
}
T& back()
{
return _con.back();
}
const T& back()const
{
return _con.back();
}
T& front()
{
return _con.front();
}
const T& front()const
{
return _con.front();
}
size_t size()const
{
return _con.size();
}
bool empty()const
{
return _con.size() == 0;
}
private:
container _con;
};
}3 priority_queue
3.1 priority_queue的介绍
1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
2. 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元
素)。
3. 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特
定的成员函数来访问其元素。元素从特定容器的“尾部”弹出,其称为优先队列的顶部。
4. 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭
代器访问,并支持以下操作:
empty():检测容器是否为空
size():返回容器中有效元素个数
front():返回容器中第一个元素的引用
push_back():在容器尾部插入元素
pop_back():删除容器尾部元素
5. 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指
定容器类,则使用vector。
6. 需要支持随机访问迭代器,以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数
make_heap、push_heap和pop_heap来自动完成此操作。
3.2 priority_queue的使用
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成
堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:
默认情况下priority_queue是大堆。
函数声明 | 接口说明 |
priority_queue()/priority_queue(first,last) | 构造一个空的优先级队列 |
empty( ) | 检测优先级队列是否为空,是返回true,否则返回false |
top( ) | 返回优先级队列中最大(最小元素),即堆顶元素 |
push(x) | 在优先级队列中插入元素x |
pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
注意:如果在priority_queue中放自定义类型的数据,用户需要在自定义类型中提供> 或者< 的重载。
我们看看这段代码:
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
friend ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
private:
int _year;
int _month;
int _day;
};
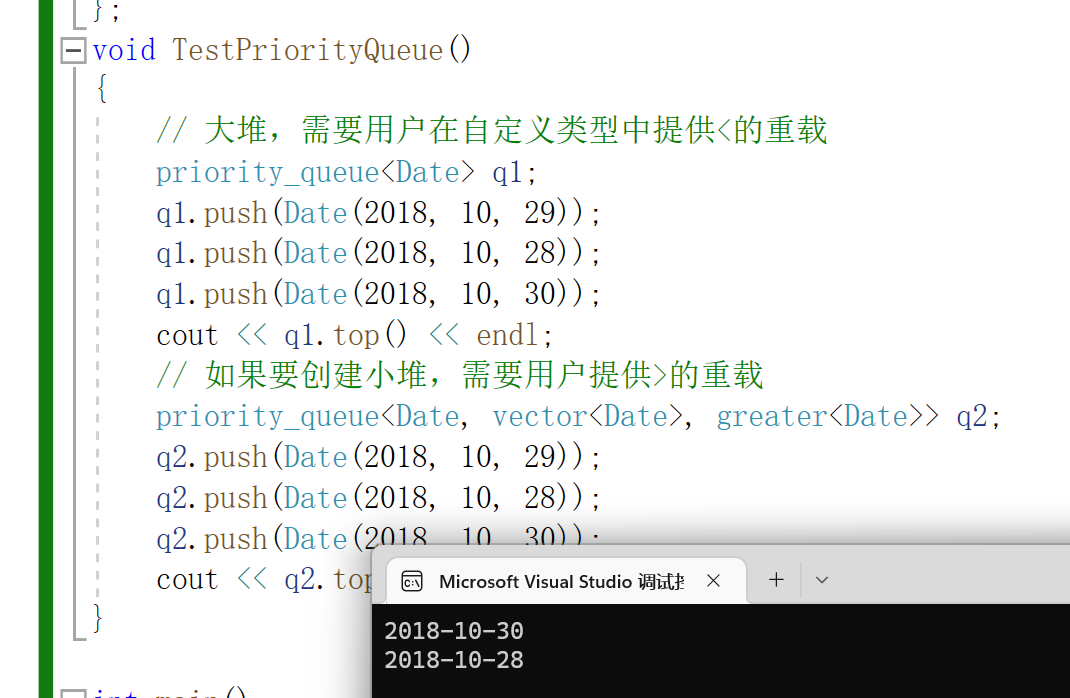
void TestPriorityQueue()
{
// 大堆,需要用户在自定义类型中提供<的重载
priority_queue<Date> q1;
q1.push(Date(2018, 10, 29));
q1.push(Date(2018, 10, 28));
q1.push(Date(2018, 10, 30));
cout << q1.top() << endl;
// 如果要创建小堆,需要用户提供>的重载
priority_queue<Date, vector<Date>, greater<Date>> q2;
q2.push(Date(2018, 10, 29));
q2.push(Date(2018, 10, 28));
q2.push(Date(2018, 10, 30));
cout << q2.top() << endl;
}
我们看看结果:
3.3 在OJ中的使用
数组中的第K个最大元素
思路1:我们可以建一个大堆,然后把前k-1个删去,最后堆顶元素就是我们想要的第k大的元素
思路2:我们可以建一个k个的小堆,然后把数组中剩下的元素依次堆顶元素比较,比它大就更新。思路2比较适合数据大的时候使用,因为这样占用的内存并不高。
思路1:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
//建一个大堆,然后删去前k-1个即可
priority_queue<int> q(nums.begin(),nums.end());
while(--k)
{
q.pop();
}
return q.top();
}
};思路2:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
//建一个k个的小堆
priority_queue<int,vector<int>,greater<int>> q(nums.begin(),nums.begin()+k);
for(int i = k;i<nums.size();++i)
{
if(nums[i] > q.top())
{
q.pop();
q.push(nums[i]);
}
}
return q.top();
}
};3.4 priority_queue的模拟实现
因为这个优先级队列的底层是一个堆的结构,在数据结构初阶的时候就已经大致的模拟实现过了:
数据结构堆的C语言实现
因为堆的底层又是一个数组实现,所以我们可以复用之前写过的vector,下面看看C++是怎么实现的
namespace liang
{
template <class T>
struct Less
{
bool operator()(T& x, T& y)
{
return x < y;
}
};
template<class T>
struct Greater
{
bool operator()(T& x, T& y)
{
return x > y;
}
};
template <class T, class container = vector<T>, class Compare = Greater<T>>
class priority_queue
{
public:
void adjust_up(int child)
{
int parent = (child-1)/2;
while (child > 0)
{
//比较父子的大小,然后判断是否交换
if (_comp(_con[parent],_con[child]))
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child-1)/2;
}
else
{
break;
}
}
}
void adjust_down(int parent)
{
int child = 2 * parent + 1;
while (child < _con.size())
{
//可能其中右孩子更大
if (child + 1 < _con.size() && _comp(_con[child],_con[child+1]))
{
++child;
}
//比较父子大小
if (_comp(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
priority_queue()
{};
template <class InputIterator>
priority_queue(InputIterator first, InputIterator last)
:_con(first,last)
{
//向上调整建堆
for (int i = _con.size() - 2 / 2; i >= 0; ++i)
{
adjust_up(i);
}
}
bool empty() const
{
return _con.empty();
}
size_t size() const
{
return _con.size();
}
const T& top() const
{
return _con[0];
}
void push(const T& x)
{
//先插入到vector的最后,然后向上调整
_con.push_back(x);
adjust_up(_con.size() - 1);
}
void pop()
{
//交换最前和最后两个,然后向上调整
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
private:
container _con;
Compare _comp;
};
void test_pq()
{
liang::priority_queue<int> q;
q.push(1);
q.push(4);
q.push(2);
q.push(6);
q.push(3);
q.push(5);
while (!q.empty())
{
cout << q.top() << " ";
q.pop();
}
cout << endl;
}
}这里使用一个 仿函数来实现比较,这样我们 就可以通过传递模板参数来实现了大小的更换。比其我们使用C语言的函数指针要方便。当然仿函数还有着一些其他的用途,后面遇到再看。
4. 容器适配器
4.1 什么是适配器
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总
结),该种模式是将一个类的接口转换成客户希望的另外一个接口。
4.2 STL标准库中stack和queue的底层结构
虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配
器,这是因为stack和队列只是对其他容器的接口进行了包装,STL中stack和queue默认使用deque:


4.3 deque的简单介绍(了解)
4.3.1 deque的原理介绍
deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和
删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比
较高。deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维
数组
我们大致画一画其中的结构:

4.3.2 deque的缺陷
这个结构确实结合了vector以及list的 优点:
与vector比较,deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不
需要搬移大量的元素,因此其效率是必vector高的。
与list比较,其底层是连续空间,空间利用率比较高,不需要存储额外字段。
缺点:
但是,deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到
某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构
时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作
为stack和queue的底层数据结构
4.4 为什么选择deque作为stack和queue的底层默认容器
1. stack和queue不需要遍历(因此stack和queue没有迭代器),只需要在固定的一端或者两端进行操作。
2. 在stack中元素增长时,deque比vector的效率高(扩容时不需要搬移大量数据);queue中的元素增长
时,deque不仅效率高,而且内存使用率高。
正是因为stack以及queue的使用不会导致deque缺点的暴露,所有stack以及queue使用它是最适合的。
5.反向迭代器(以list为例)
我们在学习和使用list的时候就会想怎么模拟实现反向迭代器呢?
其实所有的能用迭代器的容器都可以使用反向迭代器,因为 反向迭代器是通过复用正向迭代器去实现的。不管是哪个容器都是如此。下面我们看看怎么模拟实现:
通过看stl的源码我们可以发现 反向迭代器和正向迭代器竟然是对称的,而不是我们想象的差一个节点的距离(当然也可以实现)。

看看代码实现:
template<class Iterator, class Ref, class Ptr>
class Reverse_iterator
{
// 一个是T& ,一个是T*
typedef Reverse_iterator<Iterator, Ref, Ptr> Self;
public:
Reverse_iterator(Iterator it)
:_it(it)
{}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
Ref operator*()
{
//因为这里拿到的应该是反向迭代器的下一个位置
Iterator tmp = _it;
return *(--tmp);
}
Ptr operator->()
{
return &(operator*());
}
bool operator!=(const Self& it)
{
return _it != it._it;
}
private:
Iterator _it;
};我们可以看看在链表中的表现:


通过加上这两个成员函数我们就可以得到想要的结果了:
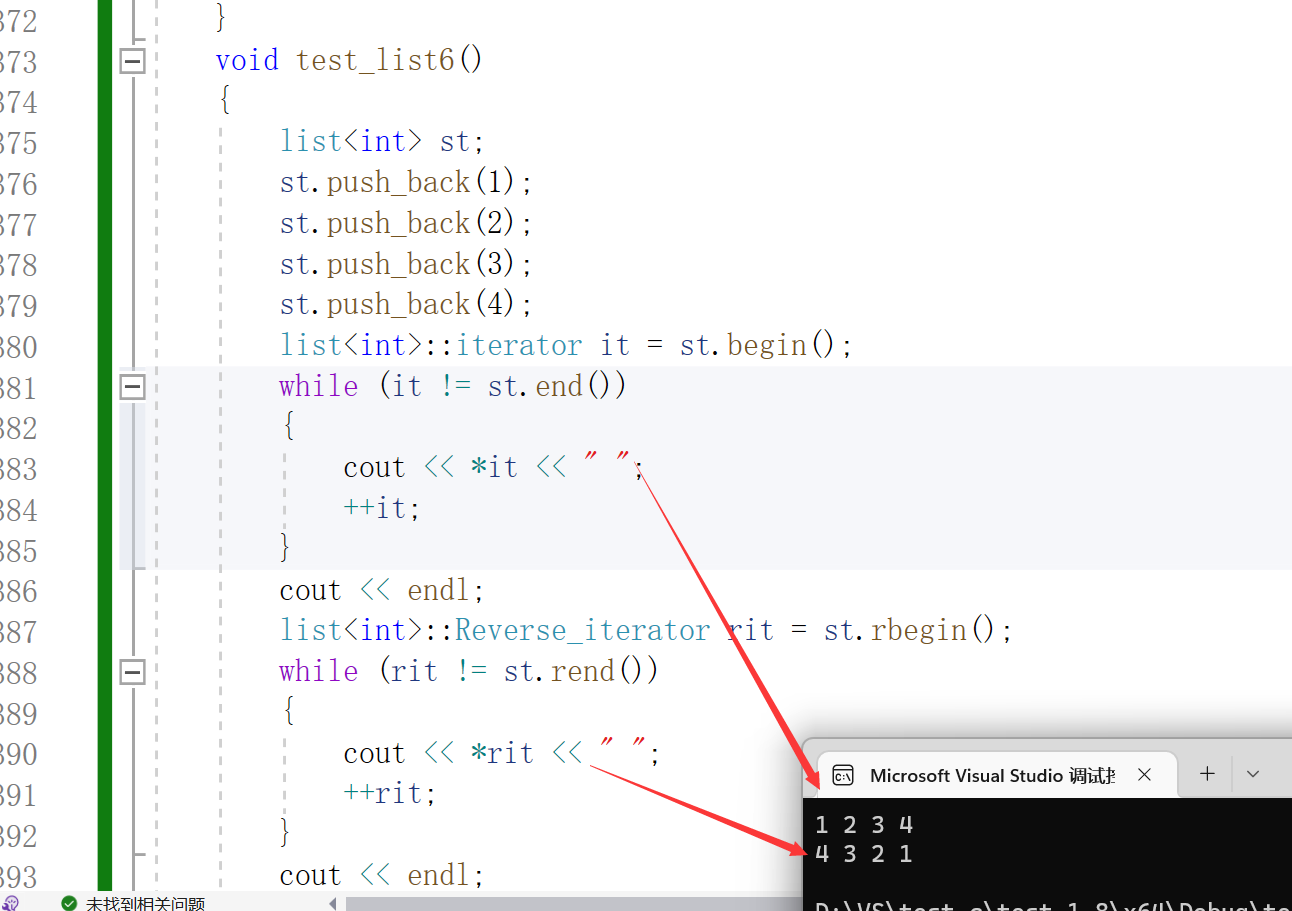
其他的容器的反向迭代器也是这样实现的。后面我们在学习使用其他容器的时候再看看结果。
栈和队列到这里就结束了:本章重点:1.stack和queue的使用,理解及模拟实现。2.优先级队列(堆)的使用及其模拟实现。3.反向迭代器的使用以及容器适配器的理解。4.仿函数的初识。