目录
1.直接插入排序
2.希尔排序
3.选择排序
4.冒泡排序
5.计数排序
6.排序总结
1.直接插入排序
(1)思想
所谓插入排序,就是将待排序数据插入到已经有序的数据中,为了使插入后数据依然有序,就要选中一个合理的位置进行插入。
(1)定义变量i,遍历待排序数据,定义遍历j,遍历已有序数据。
(2)把i指向的值存入临时遍历tmp中,遍历有序数据
(3)如果j指向的值>tmp,让j位置元素向后移动,j--;否则不移动,结束循环
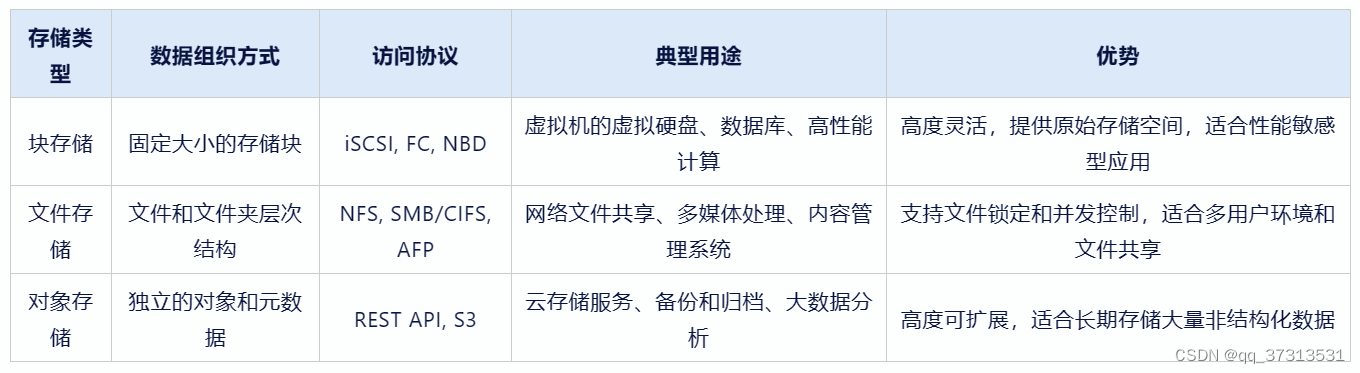
图示展示思想:

第一步:

第二步:比较,交换数据
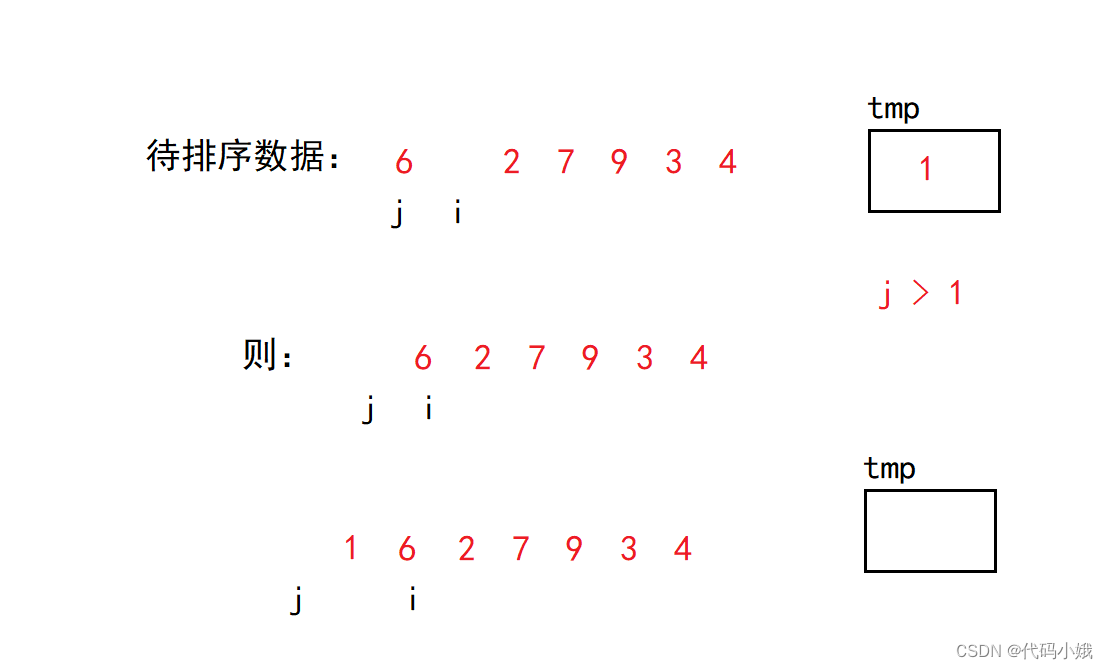
第二轮:
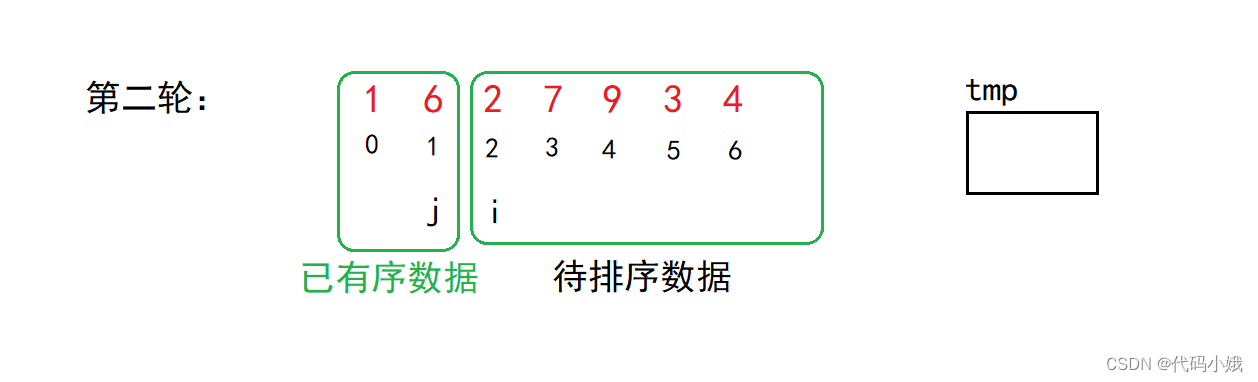

不断类推,直到有序(i走到非法位置)
(2)代码
代码需要完整,则要判断数组是否合法有数据等等,下面不做补充
public static void insertSort(int[] array) {
if(array == null) {
return;
}
if(array.length <= 1) {
return;
}
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i -1;
for (; j >= 0; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];//元素后移
}else {
break;
}
}
array[j+1] = tmp;//放回元素
}
}前面就是为给tmp找一个合理的位置,如果j<tmp,则可以提前结束循环;否则需要走完j
(3)总结
1.时间复杂度:O(N^2)。
2.空间复杂度:O(1)。
3.稳定性:稳定。
4.适应对象:元素越有序,效率越高
2.希尔排序
希尔排序就是一种特殊的直接插入排序(在它的基础上进行优化操作),比直接插入排序1效率更高。
(1)思想
1.将数据分组,每组分别进行插入排序(作为一轮)。
2.进行第二轮,缩小组距(分组后数据增加),继续进行插入排序。
3.最后一轮时,就是对原始数据进行插入排序(此时数据已经趋于有序)。
如何分组:定义一个变量gap,称为组距。也就是每间隔五个数据就有一个数据是这个组的。
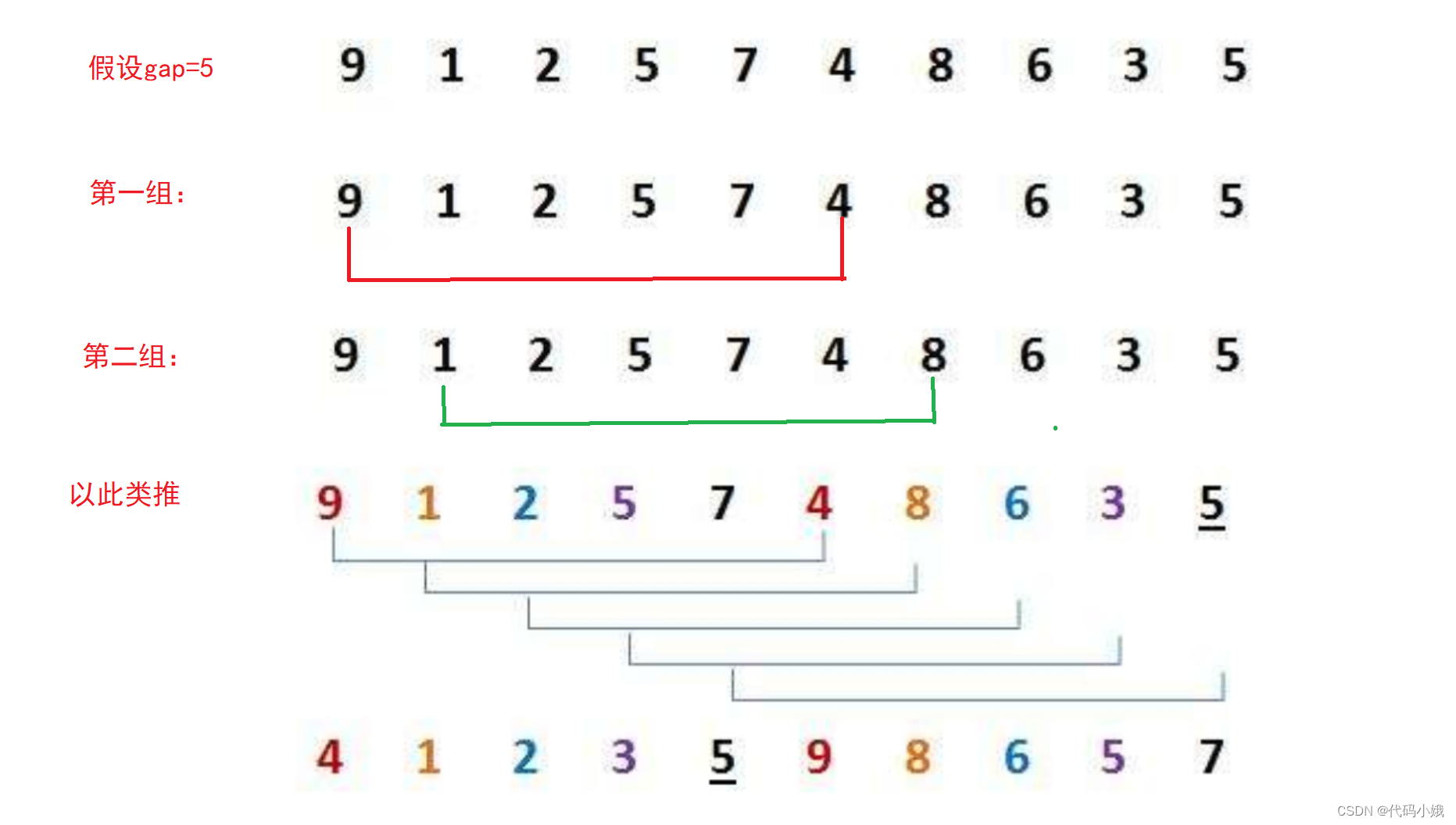
分组的间距从大到小,一开始,我们先赋值为数组的长度。下面代码的写法可以保证gap最后一次为1,完成最后的插入排序
public static void shellSort(int[] array) {
int gap = array.length;
while(gap > 1) {
gap /= 2;
shell(array,gap);//进行插入排序
}
}分组后,在组内进行插入排序即可。
如何确定:无序数据和有序数据
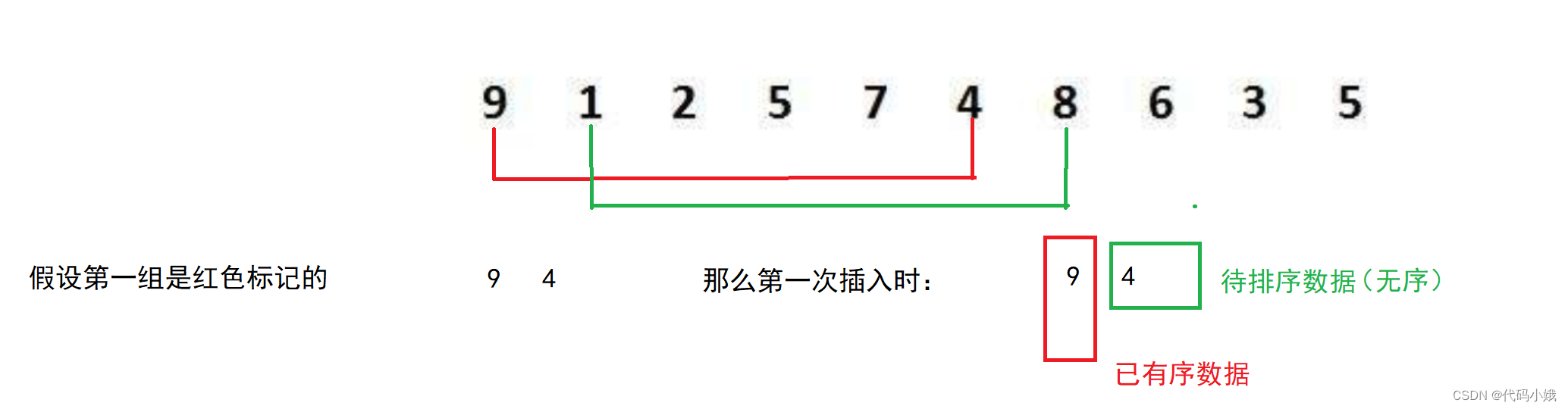
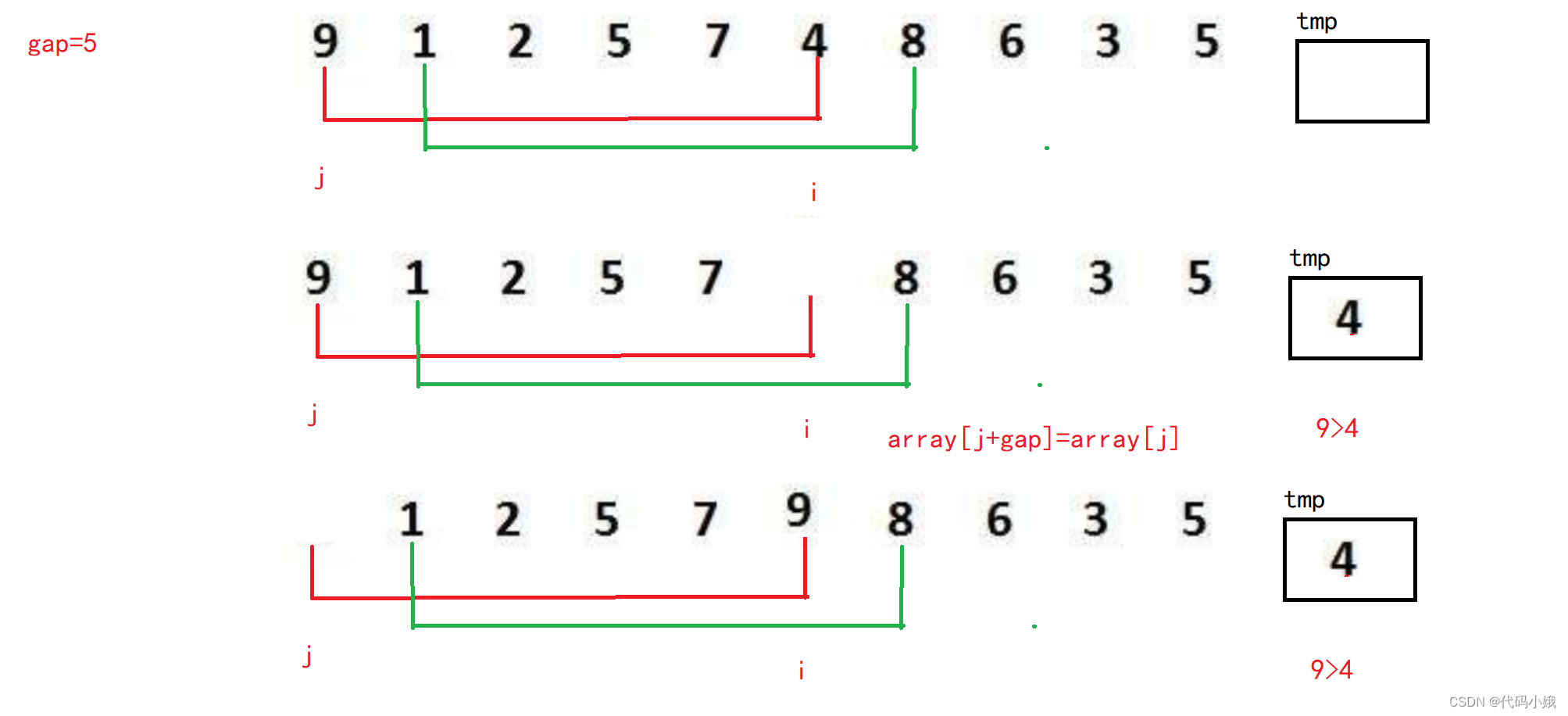
得出插入排序部分代码:
j每次移动的距离就是gap,保证在同组内移动。j循环结束代表一组的插入排序完成,进入下一轮(也就是下一组);
private static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i -gap;
for (;j >= 0;j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}
进入下一组:

(2)完整代码
public static void shellSort(int[] array) {
int gap = array.length;
while(gap > 1) {
gap /= 2;
shell(array,gap);//进行插入排序
}
}
private static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i -gap;
for (;j >= 0;j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}(3)总结
1.是对直接插入排序的优化
2.时间复杂度不好计算,暂时按:O(n^1.25)-O(1.6*n^1.25)计算
3.稳定性:不稳定
3.选择排序
选择排序思想比较简单,但是时间效率很低。每轮遍历完整个数组,找到本轮最小的放到前面;第二轮再继续遍历找到当前最小的数据再放入前面。
(1)思想
定义变量:i、j
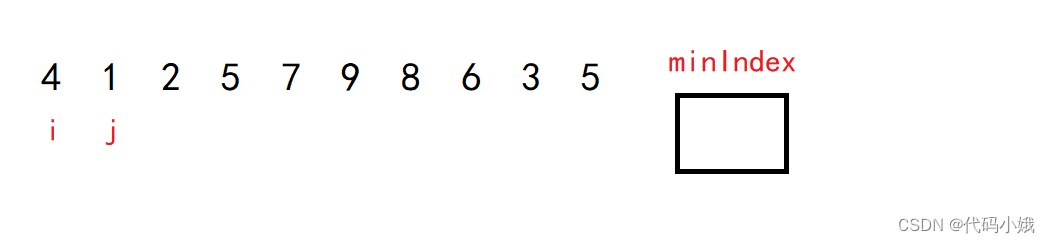
和插入排序一样定义两个变量,但是作用不同。变量i负责遍历有序数据,而变量j遍历无序数据,负责找出当前最小元素的下标(或值)。
思路图:

根据上面的思路,可以得出下面的代码
(2)完整代码
public static void selectSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
int minIndex = i;//记录当前下标
int j = i+1;
for(;j < array.length;j++) {
if(array[j]<array[minIndex]) {
minIndex = j;//最小值下标更新
}
}
swap(array,i,minIndex);
}
}
public static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}思想和代码都比较简单,就不再做简述
(3)总结
1.效率很低,实际中少用
2.时间复杂度:O(N^2)
3.空间复杂度:O(1)
4.稳定性:不稳定
4.冒泡排序
冒泡排序核心,每一轮冒泡会将当前最大的元素放到最后面。每次两个数据比较,大的数据往后走。
(1)思路
待排序数组:
int[] arr = {10,9,8,7,6,5,4,3,2,1};第一轮冒泡:

第二轮冒泡:

后续同理
(2)完整代码
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-i-1; j++) {
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
}为了应对逆序的代码,可以做出以下优化
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
boolean bool = true;
for (int j = 0; j < array.length-i-1; j++) {
if(array[j] > array[j+1]) {
bool = false;
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
if(bool) {
break;
}
}
}如果一轮比较下来,都没有发生交换,说明已经排好序了
(3)总结
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
3.稳定性:稳定
5.计数排序
适用场景(局限性):数据基本趋于一个区间内,如:待排序数据的值都是处于0-10的范围内
(1)思路步骤
第一步:求这组数据的最大值和最小值。
第二步:创建一个计数数组,大小为这批数据的差值。
第三步:遍历原数组数组,将值作计数数组的下标,该位置++。
第四步:取出计数数组,存入原数组中
(2)完整代码
public static void countSort(int[] array) {
//1.求最值
int max = array[0];
int min = array[0];
for (int i = 1; i < array.length; i++) {
if(array[i] > max) {
max = array[i];
}
if(array[i] < min) {
min = array[i];
}
}
//2.创建计数数组并初始化
int[] count = new int[max-min+1];
//3.遍历数组
for (int i = 0; i < array.length; i++) {
int index = array[i];
count[index-min]++;
}
//4.取出计数数组
int k = 0;
for (int i = 0; i < count.length; i++) {
int len = count[i];
while (len != 0) {
array[k] = i+min;
k++;
len--;
}
}
}(3)总结
(1)局限性较大,空间换取时间
(2)时间复杂度:O(范围+n)
(3)空间复杂度:O(范围)
(4)稳定性:可以稳定
6.排序总结
| 排序方法 | 最好时间 | 最坏时间 | 空间 | 稳定性 |
|---|---|---|---|---|
| 插入排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(n) | O(n^2) | O(1) | 不稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n*logn) | O(nlogn) | O(1) | 不稳定 |
| 冒泡排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(n*logn) | O(n*logn) | O(logn)-O(n) | 不稳定 |
| 归并排序 | O(n*logn) | O(n*logn) | O(n) | 稳定 |