二叉树的知识点很多，在算法刷题中需要有想象力的数据结构了。主要是用链表存储，没有数组更容易理解。在刷二叉树相关算法时，需要注意以下几点：

1. 掌握二叉树的基本概念：了解二叉树的基本概念，包括二叉树的定义、遍历方式（前序、中序、后序、层序遍历）、性质等。

2. 熟练掌握二叉树的遍历算法：熟练掌握二叉树的前序、中序、后序遍历算法，以及它们的递归和迭代实现方式。

3. 学习常见的二叉树算法题目：包括但不限于二叉树的最大深度、判断平衡二叉树、路径总和、对称二叉树等常见题目。

4. 练习二叉树的递归和迭代实现：练习使用递归和迭代方式解决二叉树相关问题，加深对算法的理解和应用。

5. 注意二叉树的性质和特点：了解二叉树的性质和特点，如完全二叉树、平衡二叉树、二叉搜索树等，可以更好地解决相关问题。

 简单介绍一下二叉树相关概念

 什么是二叉树

        二叉树是一种树形结构，每个节点最多有两个子节点（左子节点和右子节点）。根节点是位于树顶部的节点，叶子节点是没有子节点的节点。二叉树的每个节点最多有两个子节点，分别称为左子节点和右子节点。

 二叉树相关术语

• 根节点：二叉树的顶部节点称为根节点。
• 叶子节点：没有子节点的节点称为叶子节点。
• 深度：从根节点到某个节点的唯一路径上的节点数称为该节点的深度。
• 高度：从某个节点到叶子节点的最长路径上的节点数称为该节点的高度。
• 子树：二叉树中每个节点都可以看作是根节点，它的左子树和右子树称为该节点的子树。

 二叉树的遍历方式

• 前序遍历（Preorder Traversal）：根节点 -> 左子树 -> 右子树
• 中序遍历（Inorder Traversal）：左子树 -> 根节点 -> 右子树
• 后序遍历（Postorder Traversal）：左子树 -> 右子树 -> 根节点
• 层序遍历（Level Order Traversal）：逐层从上到下，从左到右遍历节点

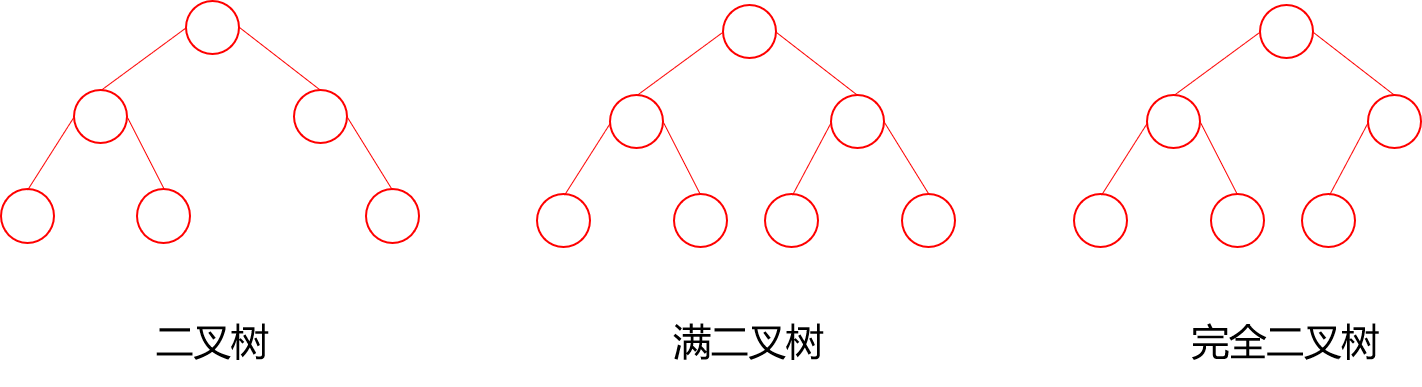
二叉树的分类

• 满二叉树：每个节点要么没有子节点，要么有两个子节点。
• 完全二叉树：除了最后一层外，每一层的节点都是满的，且最后一层的节点靠左排列。
• 平衡二叉树：左右子树的高度差不超过1的二叉树。
• 二叉搜索树（BST）：左子树上所有节点的值均小于根节点的值，右子树上所有节点的值均大于根节点的值。

二叉树的表示方式

• 链式存储结构：通过节点之间的引用关系来表示二叉树。
• 顺序存储结构：使用数组来表示二叉树，按照层序遍历的顺序存储节点。

二叉树的常见操作

• 插入节点：在二叉树中插入新节点，保持二叉树的结构特性。
• 删除节点：从二叉树中删除指定节点，保持二叉树的结构特性。
• 查找节点：在二叉树中查找指定值的节点。
• 判断是否为平衡二叉树：判断二叉树的左右子树高度差是否小于等于1，从而判断是否为平衡二叉树。

二叉树递归技巧

• 写出结束条件
• 不要把树复杂化，就当做树是三个节点，根节点，左子节点，右子节点
• 只考虑当前做什么，不用考虑下次应该做什么
• 每次调用应该返回什么

 话不多说，上题目

144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

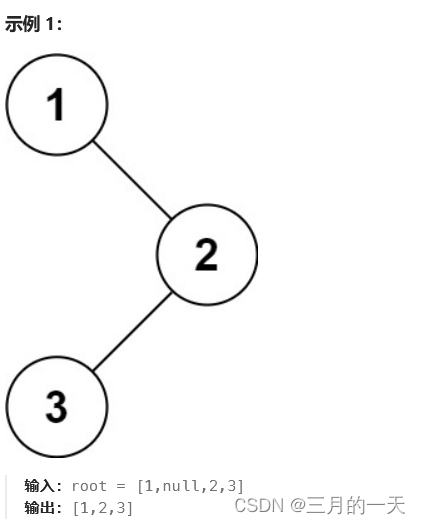
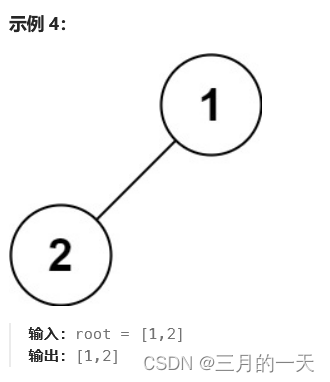
 这里需要将遍历的结果存起来，需要定义一个数组。二叉树的遍历是一个递归的过程，考虑单独建一个函数，将arr作为入参传进去。对这个函数使用递归。最后返回arr。arr是一个引用类型，所以不需要函数返回值

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function (root) {
    //定义数组存放遍历结果
    let arr = [];
    //将数组作为入参传进去
    preorder(root, arr);
    return arr;
};
function preorder(root, res) {
    if (root) {
        //前序遍历先存根节点
        res.push(root.val);
        //遍历左子树
        preorder(root.left, res);
        //遍历右子树
        preorder(root.right, res);
    }
}

 或者用数组的concat方法拼接遍历结果

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function (root) {
    if(!root)return [];
    return [root.val].concat(preorderTraversal(root.left)).concat(preorderTraversal(root.right));
};

 栈的形式

思路：从根节点开始，入栈。栈存放未遍历的节点。入栈顺序是先后后左。则出栈是先左后右。根节点在第一次出栈时已确定位置，只用考虑左右子树的入栈顺序即可

var preorderTraversal = function (root) {
    if (!root) return [];
    let arr = [];
    let stack = [root];
    while (stack.length) {
        const o = stack.pop();
        //出栈的顺序是遍历的顺序
        arr.push(o.val);
        //入栈顺序先后后左
        o.right && stack.push(o.right);
        //左子树后入栈，下次pop时先处理
        o.left && stack.push(o.left);
    }
    return arr;
};

 94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

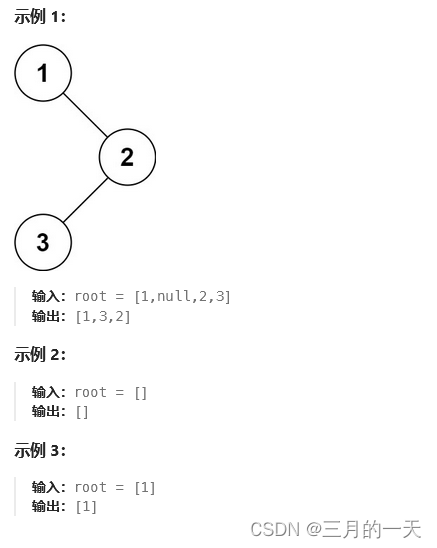
 思路：递归

先左，存根节点的val，在右

递归遍历时左右子树也会充当root，获取到val，所以只用考虑为空的时候

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function (root) {
    if (!root) return [];
    return inorderTraversal(root.left).concat(root.val).concat(inorderTraversal(root.right));
};

思路：用栈实现

遇到根节点先push进栈，去找它的左子树，一直找到最后一个左子树

这个时候就找到中序遍历的第一个节点了，也就是放在栈顶元素，将其pop出来。然后去找右子树。同理，找右子树也先找其左孩子节点。如果右节点为空，继续栈顶pop，每次pop的都是未遍历的节点。

嗯。。。这里需要手动画个树思考一下

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function (root) {
    if (!root) return [];
    const arr = [];
    const stack = [];
    let current = root;
    while (current || stack.length) {
        //每次遍历让current走到最左边
        while (current) {
            stack.push(current);
            current = current.left;
        }
        //最左边没有了话弹出当前处于最左边的叶子节点
        const o = stack.pop();
        arr.push(o.val);
        //弹出节点的右子树作为当前节点
        current = o.right;
    }
    return arr;
};

 注意：结束循环的条件是current没结束，或者栈里面还有没遍历的对象

 145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

思路：递归版本的后序遍历也是很简单的，利用数组的concat方法可以不用再新增数组进行存储。先遍历左子树，在右子树，最后是根节点，放val值。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function (root) {
    if (!root) return [];
    return postorderTraversal(root.left).concat(postorderTraversal(root.right)).concat(root.val);
};

 递归遍历相当于维护了一个隐藏的栈，如果用栈来暂存节点怎么实现？

 首先后序遍历，根节点是放在数组的最后一项，最先找到的是左子树最左边的节点。放入的顺序是【左右根左右根...根（root）】

查找节点的顺序是不是和前序遍历很像，只不过前序遍历先将根的val存起来，而后序遍历在左右子树查找完后再存。那如果换个角度思考，如果我遍历的时候遇到根节点将其放在未遍历节点的后面是不是就行了，其次是右节点放在未遍历前面，在然后是左节点放在未遍历前面。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function (root) {
    if (!root) return [];
    let arr =[];//存放后序遍历的数组
    let stack =[root];
    //后序遍历入数组的顺序是左右根，按照前序遍历的思路入栈，但是存数组的时候从数组头部插入，而不是尾部
    while(stack.length){
        const o = stack.pop();
        arr.unshift(o.val);
        o.left && stack.push(o.left);
        o.right && stack.push(o.right);
    }
    return arr;
};

 push入栈的顺序是先左在右，这样在pop的时候右子树先出栈，进数组也是先进去。

这里arr用unshift方法每次在已遍历节点的头部插入当前遍历元素

100. 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

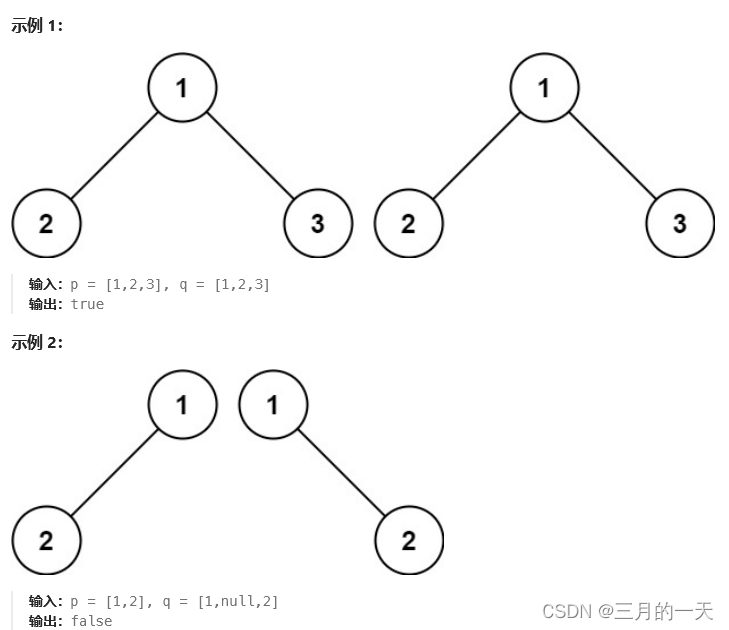
 思路：相同位置挨个比较 ；失败的时候很好考虑，即如果p和q有一个先结束，一个还没结束，说明节点个数不同，返回false；如果p和q相同节点上元素值不同也会返回false。难点在于什么时候结束？

这里可以反向思考，全部比较完，p和q同时比较完没有在比较的元素的时候，即p=null q=null。能走到这步，说明前面p和q不为空时元素都相等，返回true。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
    //当前的p和q同时为空判断为相同
    if (!p && !q) return true;
    //如果两个树有一个缺失相应的节点，返回false
    if (!p || !q) return false;
    //如果两个节点都存在，但是值不相等，返回false
    if (p.val != q.val) return false;
    //递归p和q的左子树，以及p和q的右子树
    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

 递归的思想只要将当前p和q整明白了，后面只是方法的递归调用罢了。

递归遍历p的left+q.left，拼接上递归调用p的right+q.right

101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

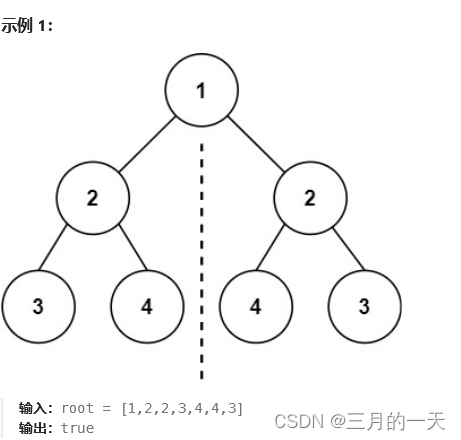
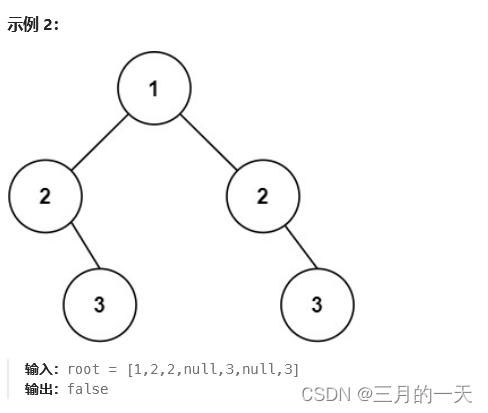
思路：跟上题类似，将数一分为二，左子树和右子树，比较左子树和右子树是否轴对称。

即左子树左节点==右子树右节点 && 左子树右节点==右子树左节点

什么情况下失败

• 左右节点一个存在，一个为nul；
• 左右节点同时存在，但val不相等。

什么情况下成功

左子树为右子树都为空，此时不需要递归，也就是叶子节点为true。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 }
 */

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function (root) {
    return checkSymmetric(root.left, root.right);
};

function checkSymmetric(leftSubtree, rightSubtree) {
    // 如果左右子树都为null则对称
    if (!leftSubtree && !rightSubtree) return true;
    // 如果左右子树有一个缺失则非对称
    if (!leftSubtree || !rightSubtree) return false;
    // 节点都存在但值不同也返回false
    if (leftSubtree.val != rightSubtree.val) return false;
    // 否则左右子树都存在，继续递归判断左子树的左节点和右子树的右节点 以及左子树右节点和右子树左节点
    return checkSymmetric(leftSubtree.left, rightSubtree.right) && checkSymmetric(leftSubtree.right, rightSubtree.left);
}

 从根节点，一分为二，将左右子树看成是两个树进行对称比较。这里肯定是要创建一个函数来递归处理左右子树

104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

这道题如果考虑到两层节点，就会复杂很多。比如将左右节点高度都考虑进去。这样提交没问题，直到看了题解，NM，1的情况可以合并在判空的时候处理。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
    if (!root) return 0;
    if (!root.left && !root.right) return 1;
    if (root.left && root.right) {
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
    if (root.left) return 1 + maxDepth(root.left);
    return 1 + maxDepth(root.right);
};

如下是简洁版本返回左子树和右子树中高度较高的那个+1，如果不存在返回0

简化版本再次印证了递归的的技巧：只考虑根左右三个节点的树！！！如果左子树或右子树有孩子进入下次递归就行了

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
    if (!root) return 0;
    return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
};

世界都清爽了。注意tips：尽量使用Math提供的方法，提示逼格，减少代码量

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

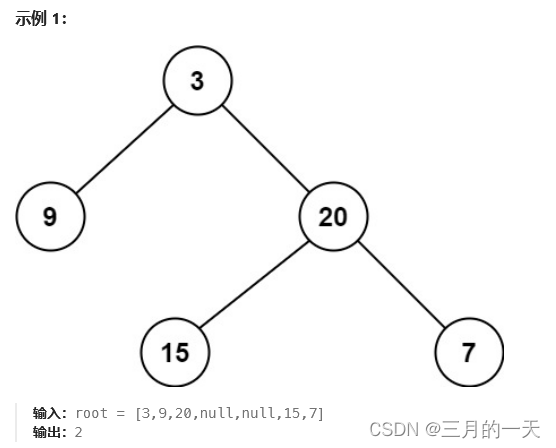
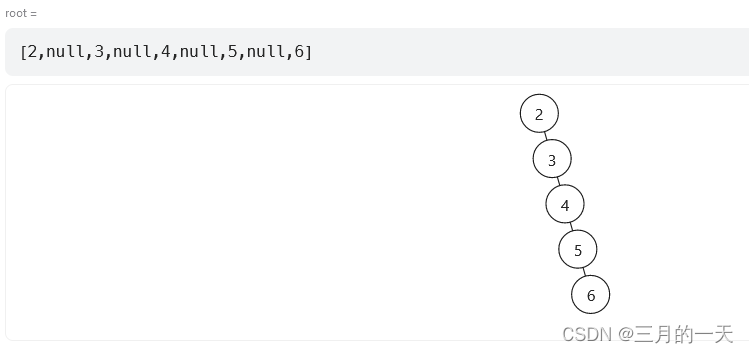
思路：分析题目

1. 如果同时存在左右子树，最小深度是左右子树的最小深度和+1
2. 如果只存在左子树或右子树，最小深度等于左子树或右子树的深度+1
3. 如果当前不为空，左右子树为空，返回1
4. 如果是空则，返回0

其中2和3可以合并

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function (root) {
    if (!root) return 0;
    if (root.left && root.right) {
        return 1 + Math.min(minDepth(root.left), minDepth(root.right));
    }
    return 1 + minDepth(root.left || root.right);
};

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

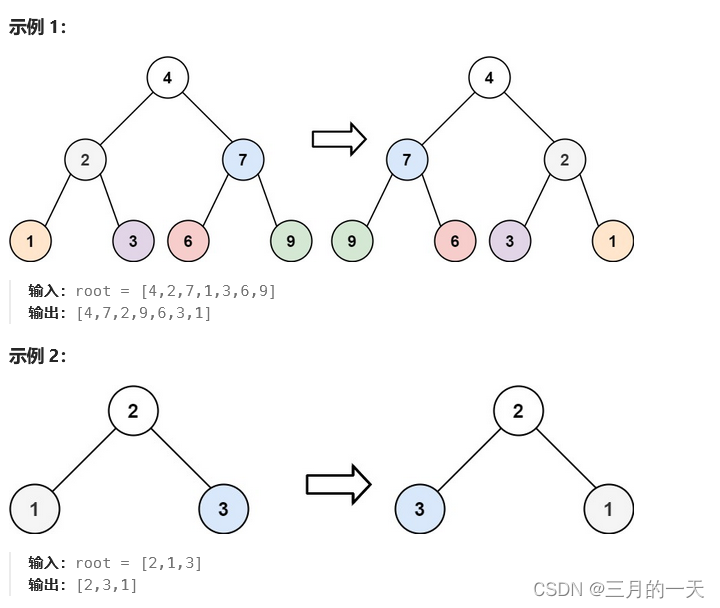
 思路：交换节点，根节点固定，交换左右

只用看示例2，只有三个节点的树。看下递归怎么解决

首先交换1和3，因为二叉树是指针串起来的，交换两个的地址指向就好了。

1变成3，需要先将3的信息暂存起来。

将暂存的3替换1

根节点交换完成，在递归处理根的左子树，右子树。

在递归处理，也就是第二次处理时，左子树的节点充当root，右子树的节点也会充当root

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function (root) {
    if (!root) return null;
    let temp = root.left;
    root.left = root.right;
    root.right = temp;
    invertTree(root.left);
    invertTree(root.right);
    return root;
};

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

 

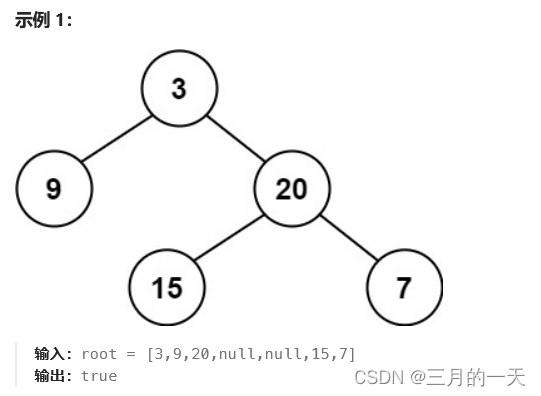
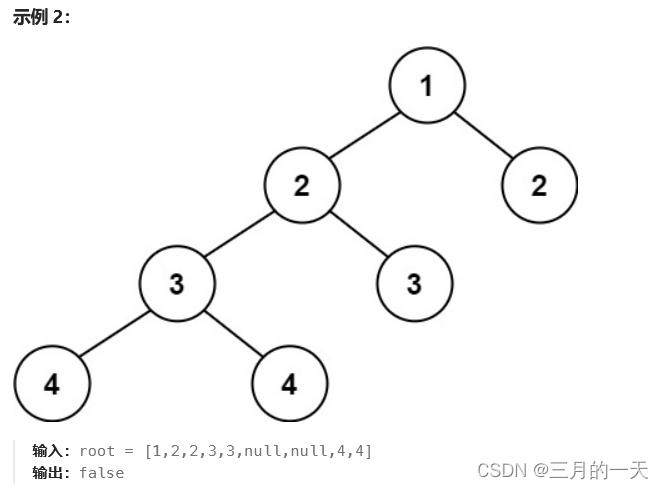
思路：注意解题，题目说的每个节点的左右子树高度差不能超过1

继续利用递归处理。简单来说，先创建一个方法用于计算某个子树的高度。在将根节点的左右子树高度进行计算，如果根节点的左右子树高度差大于1则返回false。（只考虑根节点能通过90%的用例）

最后要判断，左右子树是否也满足高度相差1。像下面的示例，虽然根节点满足了，但是下面的2的左右高度差为2不满足。

/**
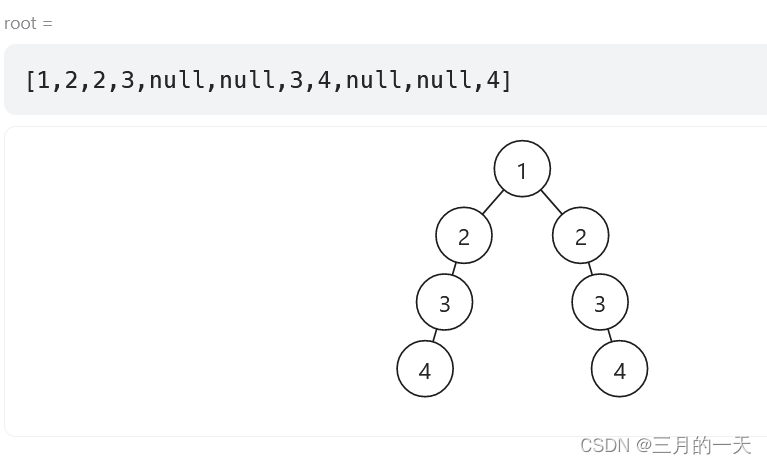
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function (root) {
    if (!root) return true;
    if( Math.abs(getHeight(root.left) - getHeight(root.right)) > 1){
        return false;
    }
    return isBalanced(root.left) && isBalanced(root.right);
};
function getHeight(node) {
    if (!node) return 0;
    return 1 + Math.max(getHeight(node.left), getHeight(node.right));
}

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

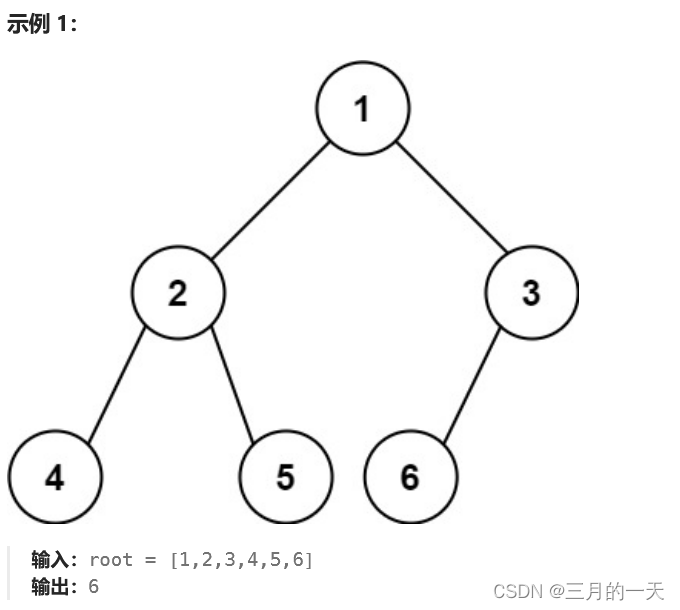
 思路：这道题最笨的方法可能是递归找所有的节点，统计个数。

然而要利用这道题的结构，完全二叉树，我们在学习数据结构的时候，完全二叉树有个特性，就是高度如果为h，那么h-1层一定铺满，或者说h-1层一定是满二叉树。

这道题求节点总数，如果按层来看，不好处理。

换个角度，从中间砍一刀，一分为二，左右子树。

可以发现，完全二叉树就分两种

• 一种是左子树第h层铺满，但右子树没铺满
• 另一种是左子树h层有节点，而右子树h层没有

为什么这么看呢？

两种情况分别可以确定左子树的个数、右子树的个数

对于未确定的右子树或左子树可以采用递归方式处理

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function (root) {
    if (!root) return 0;
    let leftHeight = getHeight(root.left);
    let rightHeight = getHeight(root.right);
    //左右高度相等，左子树是满二叉树，个数=2^高度-1  别忘了根节点+1
    if (leftHeight == rightHeight) {
        return Math.pow(2, leftHeight) + countNodes(root.right);
    }
    //左子树大于右子树，右子树是满二叉树，个数=2^右子树的高度-1 加上根节点+1
    return Math.pow(2, rightHeight) + countNodes(root.left);
};
function getHeight(node) {
    if (!node) return 0;
    return 1 + Math.max(getHeight(node.left), getHeight(node.right));
}

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

思路：使用深度优先搜索（DFS）算法来遍历二叉树，并在遍历的过程中记录从根节点到叶子节点的路径。深度搜索递归结束条件是找到叶子节点，将路径信息打印到result中。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function (root) {
    if (!root) return [];
    let result = [];
    dfs(root, [], result);
    return result;
};
//深度遍历递归方式，携带路径信息，result结果信息
function dfs(root, path, result) {
    if (!root) return;
    path.push(root.val);
    if (!root.left && !root.right) {
        //碰到叶子节点结束递归
        result.push(path.join('->'));
    } else {
        //进行递归，将当前路径信息带入，注意浅拷贝当前路径信息
        dfs(root.left, path.slice(), result);
        dfs(root.right, path.slice(), result);
    }
}