Multi-Compartment Electric Vehicle Routing Problem for Perishable Products
ABSTRACT
该研究首先提出了一个异质车队、多车室的易腐产品电动汽车路由问题(MCEVRP-PP)。我们捕捉到MCEVRP-PP的许多实际需求和限制,如多个温度区、硬时间窗口、在交付过程中充电一次以上、每单位制冷的各种功耗等。我们将MCEVRP-PP建模为一个混合整数程序,旨在优化总成本,包括车辆固定成本、电力成本和冷却成本。开发了一种混合蚁群优化(HACO)来解决这个问题。在转移规则中,引入了时间窗口以提高路线构建的灵活性。根据多隔间电动汽车的特点,在路线建设中开发了容量约束判断算法。设计了六种带有时间窗口、充电站等的局部搜索策略。基于各种实例的实验验证了HACO比蚁群优化(ACO)更有效地解决了MCEVRP-PP。与燃油车和单室车相比,电动车和多室电动车可以节省总成本和里程数,并提高车辆的利用率。
过去,零售商主要使用燃油车运输易腐产品。正如我们所知,燃油车是温室气体排放的主要来源之一。易腐产品需要冷藏设施(冷藏),以在运输过程中保持新鲜度和可用性。制冷消耗大量能源。因此,FV对环境的影响更为显著[4,5]。随着近年来电动汽车技术的快速发展,零售商现在可以选择使用电动汽车。电动汽车是最清洁的交通工具之一,因为它们可以由可持续和可再生能源提供动力。它们没有本地温室气体排放,只产生最小的噪音。后两个方面在交通拥堵频繁的城市地区尤为重要[6]。此外,定义为零排放的电动汽车能够达到排放目标。因此,使用电动汽车进行城市配送是大势所趋。尽管近年来电动汽车的动力电池技术发展迅速,但由于低温导致的电池衰减,续航里程将进一步缩短,尤其是在冬季。因此,可用范围可能不足以在一次运行中执行物流服务提供商的典型交付之旅。由于减少一辆车的交付次数不是一个有利可图的选择,因此需要前往沿途的公共充电站。有必要在路线规划中考虑充电,以避免低效的车辆路线和长弯路,特别是在可用充电站数量稀少的情况下。多室电动车可以节省总成本和里程数,并提高车辆的利用率。
尽管近年来电动汽车的动力电池技术发展迅速,但由于低温造成的电池衰减,驾驶里程将进一步减少,特别是在冬季。因此,可用的范围可能不足以在一次运行中执行物流服务提供商的典型交付之旅。由于减少一辆车执行的交付数量不是一个有利可图的选择,因此需要访问沿线的公共充电站。有必要考虑路线规划中的充电问题,以避免低效的车辆路线绕行,特别是在可用的充电站数量稀少的情况下
在本文中,我们首先提出了一个易腐产品的异构车队、多隔间电动汽车路径问题(MCEVRP-PP)。目前还没有关于具有多个车厢和异构车队的电动汽车路线问题(EVRP)的研究,尤其是对于易腐产品。在MCEVRP-PP中,电动汽车的能耗率与电动汽车的重量呈线性关系。每个商店都有一个硬时间窗口,这意味着每个商店的服务开始时间不能晚于其时间窗口。由于每个隔间都安装了冷却系统,因此可以调节每个隔间的温度。每个隔间可以专用于任何温度区域。电动汽车在行驶过程中可以根据需要多次访问充电站。针对MCEVRP-PP,建立了一个混合整数规划模型,旨在最小化总配送成本,包括车辆固定成本、电力成本和制冷成本。考虑到所提出问题的NP难性,开发了一种混合蚁群优化(HACO)来求解MCEVRP-PP。
本研究的贡献可以总结如下:
(1)我们将多隔间电动汽车引入到易腐产品的车辆路径问题(VRP)中。我们提出了MCEVRP-PP,它考虑了多个温度区、异构车队、多隔间电动汽车、硬时间窗口、交付过程中的充电、与负载线性相关的能耗率等。建立了MCEVRP的数学规划模型。
(2) HACO是为解决MCEVRP-PP而开发的。我们在算法中引入了六种局部搜索策略,以解决VRP更复杂的问题结构。
(3) 我们使用两个新设计的MCEVRP-PP实例集验证了HACO的性能。在进一步的实验中,我们表明,就总成本而言,多隔间的电动汽车总是优于多隔间的FV或单隔间的电动车辆。
本文的其余部分组织如下:第1节概述了与本研究相关的现有工作。第2节给出了MCEVRP-PP的形式化定义和数学模型。第3节介绍了算法设计过程。该算法通过大量的数值实验进行了测试。实验设计和相应的结果见第4节。最后,第5节总结了主要发现。
1.相关工作
1.1 VRP
1.2 EVRP
EVRP是VRP的一种变体。为电动汽车制定可行的分销计划需要考虑电动汽车的特点,如续航能力、充电能力等。Bruglieri等人[29]以最短里程、最短充电时间和最少车辆为目标对电动汽车回收计划进行了建模。针对这一问题,设计了一种分支变邻域搜索算法。电动汽车的主要特点之一是电源是电能。充电策略影响EVRP解决方案。在Keskin和Çatay[30]的研究中,充电站根据充电策略确定充电量。Erdem和Koç[31]也考虑了充电状态。Erdelić等人[32]针对EVRPTW问题提出了混合单一充电策略和多种充电策略的策略。就充电速度而言,有三种充电策略可供选择:快速充电、正常充电和慢速充电[33]。在充电程度方面,有两种策略:完全充电和部分充电[30]。线性函数和非线性函数是充电量和充电时间的两种关系[34-36]。从允许充电次数来看,可分为单次充电和多次充电[32]。在这项研究中,电动汽车被允许在途中充电一次,并且假设在快速策略下,每次充电都将以恒定的速率充满。此外,Verma[37]在EVRPTW中考虑了充电和电池交换,并假设可用的站既是充电站又是电池交换站。电动汽车的续航里程比燃油车短。因此,能源消耗是当前EVRP的研究热点。大多数研究假设电动汽车的能耗与里程之间存在线性相关性。然而,加速度、负载和速度等其他因素也与能耗有关[38]。在Goeke和Schneider的[39]关于EVRP的研究中,负载对能耗的影响受到了关注,而Zhang等人[40]考虑了随机和未优化的速度、斜率和其他因素。肖等人[41]将能量消耗率(ECR)引入EVRPTW,并将ECR视为速度和负载的联合非线性函数。
1.4 总结
到目前为止,还没有关于多室电动汽车与异质车队在易腐产品VRP中的应用的文献。在这项研究中,具有多个隔间的异质电动汽车首次被应用于易腐产品的分配。易腐产品的燃料VRP经常考虑衰变损失和碳排放。而在我们的MCEVRP-PP中,没有必要考虑产品恶化和碳排放,而是考虑分配过程中公共充电站的制冷能耗和充电等要求。这些要求大大增加了解决问题的复杂性。
2. 问题描述和公式
DC负责向杂货店运送各种易腐产品。我们定义了一组杂货店。0,并且是DC。0并且分别表示EV离开DC和EV返回DC。在实践中,电动汽车在一次旅行中可能会多次访问同一充电站。在数学模型中,我们引入了虚拟充电站,它是真实充电站的副本。确保在一次旅行中最多访问一次充电站。我们定义了一组真实和虚拟充电站。该问题定义在一个具有弧集的完全有向图上。每个弧都与非负距离和行进时间相关联
M表示积段的集合。需要相同温度的易腐产品可以在同一隔间内运输,它们构成一个产品段。这个集合表示一个异质的电动车队,它为.NET中的商店运输易腐产品。每辆电动车由多个隔间组成,不同车辆的隔间数量是相同的。D是车辆的隔间集合。每个隔间只用于一个乘积段。由于每个隔间都安装了冷却系统,隔间可以专门用于任何产品段。这意味着车辆中的不同隔间可以携带相同的产品段。车辆的隔间容量为(kg)。每辆电动车的电池容量为(kW∙h)。一辆电动车带着完全充电的电池离开直流电,返回直流电。当车辆在运输过程中处于低电量时,可以在充电站多次充电,每次对电池完全充电。我们假设充电率为(kW),并且是恒定的。使用车辆的固定成本是(RMB)。单位功耗成本为(RMB/(kW∙h))。所有的商店都需要由一个有一些订单的车辆来访问。对于每个存储,硬时间窗口表示为 。(h)表示存储中的服务时间。每个商店对各种产品段的订单是已知的。让我们表示商店的产品段的顺序,并表示的数量。这个顺序可以由任何车辆的任何隔间来满足。对于任何.每个订单不能被分割,只能由一个隔间提供。此外,商店可以对部分产品段进行排序。当 ,意味着商店对产品段没有订单
每一个行进的电弧都消耗电池电量。首先,有轨电车是由电力驱动的。假设车速恒定,忽略坡度和路面等因素,车辆单位里程的功耗与车辆重量呈线性关系。因此,电动汽车每公里的功耗可以通过以下公式表示,其中和是参数,表示车辆上的负载。由于配送过程中的订单交付会使车辆负荷逐渐降低,因此路线各弧段车辆的单位功耗也会逐渐降低。其次,需要电能制冷来将产品段保持在相应的温度。假设外部环境温度是固定的,冷藏室每单位时间消耗的电能与冷藏室的温度区和空间大小有关。温度区越低,空间越大,单位时间制冷消耗的电能就越高。令表示产品段m的车辆k的车厢d中每小时的电能消耗。由于车厢的大小是固定的,因此是恒定的和已知的。制冷成本与制冷时间有关,制冷时间是在运输卸载、充电和等待过程中产生的。需要注意的是,在分配过程中,只要隔间是空的,就没有必要冷藏。MCEVRP-PP的集合、参数和变量如表1和表2所示。
我们将MCEVRP-PP建模为数学程序,如下所示:
1) 目标函数
目标是最小化由三个项组成的总成本。第一个项是与所使用的每辆车有关的固定成本;第二个项是车辆功率成本;第三个项是制冷成本。方程(1)和(4)是目标函数。
(2) 车辆路线约束
约束(5)确保每个商店只能被访问一次。约束条件(6)确保了路线的连续性。约束条件(7)保证每辆车离开DC并返回DC。每辆车最多只有一次行程。约束条件(8)保证不是所有的充电访问顶点都必须使用
(3) 车辆装载约束
约束(9)和(10)确保隔间内的乘积之和不超过隔间容量。约束条件(11)和(12)跟踪隔间内的剩余负荷,并保证所有商店的需求都得到满足
4) 时间约束
d k i j arc (i ;j ) i i k i l i 公式(13)和(14)确定了车辆隔间被清空的时间。约束条件(15)分别表示节点之间的时间关系和何时存储、直流、充电站。同时,约束条件(16)表示充电站时的时间关系。方程(17)决定了车辆离开商店的时间。约束条件(18)确保到达时间早于时间窗口。
(5) 车辆功率约束
弧(i ;j )i 约束条件(19)−(21)分别确保车辆剩余功率在存储、直流、充电站时为负值。
6) 决策变量
约束条件(22)确保每个订单只由一个隔间交付。约束条件(23)和(24)代表变量之间的关系。约束条件(25)保证每个隔间最多加载一个产品段。该隔间允许为空。方程(26)是对决策变量的范围约束。
4. 实验结果
实验中的实例集改编自MCEVRP-PP的Solomon基准实例。为了验证HACO的有效性,我们进行了三个实验。每个小规模的实例分别包括5、10和15家商店。每个商店规模有12个实例。有56个大规模的实例,每个实例包括100个商店。根据商店分布的特点,实例被分为3种类型。聚类(C)、随机(R)和随机&&聚类(RC)分布。
为了验证HACO的性能,我们进行了三个实验。在第一个实验中,我们分别选择了3种类型的6个小销售实例和35个大规模实例来验证HACO的效率和正确性。并且我们比较了每种局部搜索策略在大规模实例中的表现。在第二和第三个实验中,我们将FVs与EVs进行比较,并将单室车辆与多室车辆进行比较。
HACO是用Python 3.7编码的,在一台装有Core i4-4210U,4GB内存的计算机上进行。
4.1参数设置
实验中,产品段被设定为三种:环境、冷冻和冻结。车辆隔间的数量与产品段的数量相同。车辆容量和电池容量的参数是根据Solomon的实验数据改编的。车队由两个模型组成。对于每个模型,每个隔间的容量是相同的,电能消耗的参数: , 。单位耗电成本、行驶速度和充电率。对于模型1, , , 和 。对于模型2, , , , 和 。根据实际情况,对于模型1,我们分别为环境、冷冻和冷冻设置了0.5千瓦、1千瓦和1.5千瓦。对于模型2,我们分别设定为2千瓦、2.5千瓦和3千瓦。ACO的相关参数是根据目前的研究设定的,详见表3。
4.2 小规模实例的研究
我们使用ACO和HACO在18个小规模实例上求解MCEVRP-PP。ACO和HACO分别为每个实例执行10次运行。结果如表4所示。列ACO和HACO分别是使用这两种算法的最佳解决方案的总成本。与ACO相比,HACO的成本降低百分比如列所示。结果表明,HACO有效地解决了所有MCEVRP-PP实例。对于5个和10个商店的实例,ACO和HACO可以找到相同的最优解。然而,增加的存储导致高计算复杂度。对于15家商店的例子,ACO很难找到更好的解决方案,而且往往停滞不前。局部优化可以改进解决方案。

4.3 对大规模实例的研究
为了验证每个局部优化策略的有效性,我们首先从大规模实例中随机选择六个实例,并结合局部搜索策略使用ACO进行求解。我们通过Relocate、Reverse、Exchange、TimeGreedy、Worst Customer和2-opt等不同策略捐赠算法。对于每个实例,每个算法执行10次运行。图1显示了成本降低最高的结果。该列表示与ACO相比的成本降低百分比。结果表明,对于大规模实例,Relocate、Reverse、Worst Customer和2-opt可以有效地解决问题。2-opt表现最好,因为充电在交付中很重要,与公共充电站相关的策略可以有效地改进解决方案。Exchange和TimeGreedy无法改进解决方案。因此,我们注意到ACO结合了四种性能更好的策略的算法,即HACO-I。
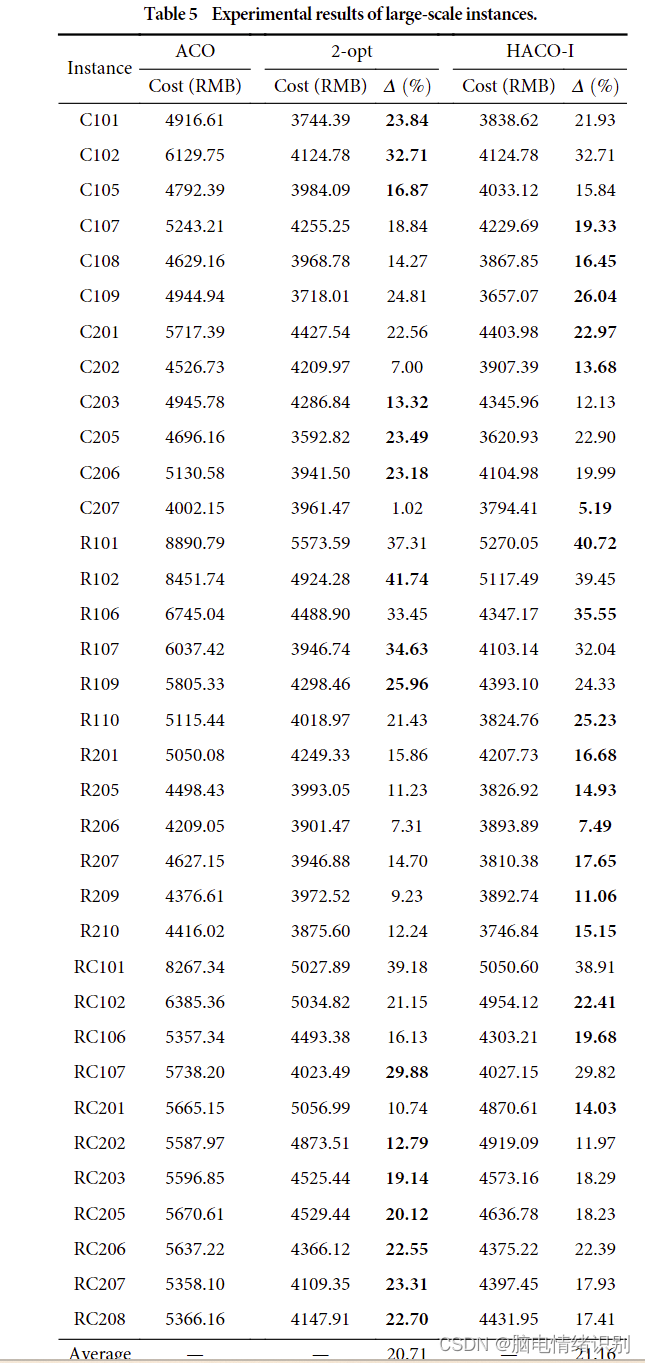
为了分析HACO-I、ACO、Relocate、Reverse、Worst-Customer、2-opt和HACO-I的性能,在剩下的29个大规模实例上进行了10次运行。每种类型实例的平均成本降低百分比显示在图中。2.而ACO、2-opt和HACO-I的详细实验结果见表5。
从结果中,我们发现有五种算法可以改善所有类型实例的解决方案。2-opt和HACO-I改善了所有的实例,并优于Relocate、Reverse和Worst-Customer。2opt和HACO-I的平均成本降低百分比分别为20.71%和21.16%。Relocate和Reverse的改进不太有效。WorstCustomer的表现最差。我们注意到,2-opt在一半的实例中比HACO-I表现得更好。这表明结合四种局部搜索策略的ACO在某些情况下比结合2-opt策略的ACO表现更差。造成这种情况的可能原因如下。(1)其他策略,特别是最差客户,对HACO-I的干扰;(2)迭代时间不够,HACO-I的优势没有得到充分体现
4.4 电动汽车和FV的比较
在实验中,我们比较了两个车队。电动汽车和FVs。电动汽车和FV有两种类型的车辆。对于FVs,一个隔间的数量和容量与EVs相同。对于模型1,油箱的容量为100L,电池的容量为100千瓦∙h,固定成本为200人民币。对于模型2,油箱的容量为120L,电池的容量为120千瓦∙h,固定成本为300人民币。单位燃料消耗成本为5.5元/升。
五结论:
在本研究中,我们基于冷链物流的实际需求,提出了一个易腐产品的异构车队、多隔间电动汽车路径问题,称为MCEVRP-PP。我们构建了一个混合整数规划模型,以最小化总成本。每辆电动汽车在交付过程中都可以多次充电。未固定的隔室温度可以调节,以满足任何产品细分市场的要求。每公里的功耗与负载呈线性关系。车厢空着的时候没有冷藏。上述考虑使研究更加现实。HACO就是为了解决这个问题而设计的。为了提高算法的性能,我们在传输规则中引入了时间窗口匹配因子,根据MCEVRP-PP的特点设计了一种容量约束算法,并根据时间窗口和充电站提出了六种局部搜索策略。该算法通过各种实验进行了验证,包括小规模实例和大规模实例。为了测试每种局部搜索策略的性能,我们分别将HACO与ACO以及ACO与单个策略相结合进行了比较。实验结果表明,HACO算法优于ACO算法,特别是在大规模实例中。最后,我们将电动汽车与FV进行比较,并将MCV与SCV进行比较。结果表明,电动汽车和MCV可以有效地降低总成本,同时电动汽车的里程数也在增加。
我们假设每个客户对不同的产品细分市场都有相同的时间窗口,并且在研究中每个客户最多只能访问一次。但事实上,客户可能对不同温度区域的产品有不同的时间窗口偏好。例如,超市可能想在早上收到冷冻食品,其他类型的商品可以稍后送达。未来的研究将考虑客户对时间窗口的偏好,这属于多时间窗口问题。此外,我们假设车厢的数量与产品细分市场的数量相同,并且所有车辆都是多车厢车辆。未来的研究可以考虑单车厢车辆和多车厢车辆的组合进行分配