参考文献：

1. [GDL+16] Gilad-Bachrach R, Dowlin N, Laine K, et al. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy[C]//International conference on machine learning. PMLR, 2016: 201-210.
2. [HTG17] Hesamifard E, Takabi H, Ghasemi M. Cryptodl: Deep neural networks over encrypted data[J]. arxiv preprint arxiv:1711.05189, 2017.
3. [LKL+22] Lee J W, Kang H C, Lee Y, et al. Privacy-preserving machine learning with fully homomorphic encryption for deep neural network[J]. IEEE Access, 2022, 10: 30039-30054.
4. 安全多方计算与同态加密初探 - 知乎 (zhihu.com)
5. 激活函数其实并不简单：最新的激活函数如何选择？ - 知乎 (zhihu.com)

Privacy-Preserving Machine Learning（ PPML）的任务是安全的实现模型的训练和预测。可以采用的隐私计算技术包括：

• 全同态加密（FHE），
  • 场景：单个客户拥有数据，云服务器提供已训练好的模型，做预测
  • 优点：通信开销较小，客户可以离线，IND-CPA 安全
  • 缺点：计算复杂度较高
• 多方安全计算（MPC），
  • 场景：多个客户拥有数据，云服务器和它们执行 MPC 协议，做训练和预测
  • 优点：计算速度较快，被动安全/主动安全
  • 缺点：通信开销很大，客户必须在线，模型泄露攻击，信任问题
• 差分隐私（DP），
  • 场景：云服务器拥有数据，利用 DP 自行训练出带噪的模型，发送给客户
  • 缺点：只能用于训练，安全性较弱
• 联邦学习（FL），
  • 场景：多个客户拥有数据，云服务器根据它们发送的预处理数据，做训练
  • 缺点：只能用于训练，安全性较弱

CNNs

Convolutional Neural Networks 是一种特殊的前馈网络，包含若干层有序的神经元，

1. input layer
2. hidden layer
3. Convolutional Layer：卷积核 + 步幅，整合邻域的信息
4. Activation Layer：激活函数，包括 Sigmoid, Tanh, ReLU 及其变体，获得非线性回归能力
5. Pooling Layer：下采样，主要包括 max pool 和 mean pool，减小数据/模型的规模
6. Fully Connected Layer：关于权重的矩阵乘，将神经元的输出线性组合
7. Dropout Layer：随机将某些神经元的输出置为零，防止过拟合
8. output layer

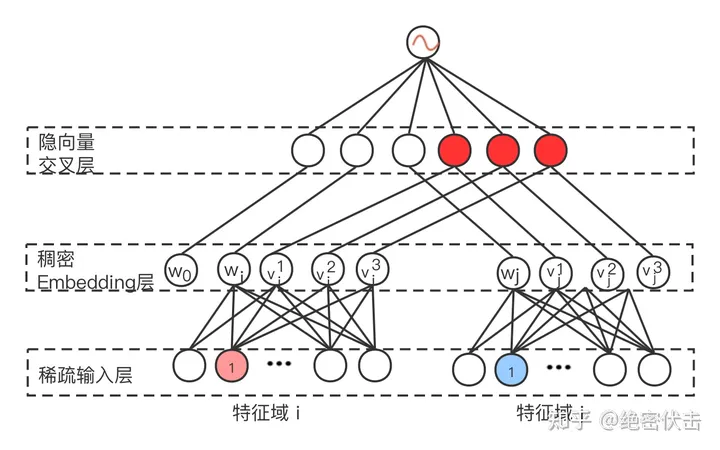
如图所示，

CryptoNets

[GDL+16] 提出了 CryptoNets 模型，他们仅关注推理，模型是明文训练的。他们使用 SEAL 库中的 YASHE 方案（有实现么？）。在 MNIST 数据集上，预测精度为 $99\%$，吞吐率是每小时 58982 次预测，单次预测的延迟是 250 秒。

编码方式

由于 YASHE 是基于 NTRU 假设的 Level FHE，明文空间是 $R_t={\mathbb{Z}}_t[X]/(X^N+1)$，但是神经网络中的数据都是浮点数。[GDL+16] 提出可以组合使用 SIMD 打包以及 CRT 技术：选取若干个 NTT-friendly 的不同素数 $t_1,t_2,\cdots ,t_k$，那么就有 $R_{{\prod }_i{t}_I}\cong {\prod }_i{R}_{t_i}$，只要让 $t^{\ast }={\prod }_i{t}_i$ 充分大，那么就可以将指定精度的定点数转化为整数，且计算过程中不会出现取模 $t^{\ast }$ 而导致错误。

网络结构

因为第二代 FHE 适合计算大批量的整数算术，因此 [GDL+16] 修改了 CNNs，

1. 标准的激活函数都是非算术的，他们修改为使用 $x^2$ 作为激活函数
2. 最大池化难以表示为低次多项式，因此采用**（缩放的）均值池化**，只计算加和，并不计算除法，额外的因子在下一层中处理
3. 卷积层、全连接层、均值池化都是线性变换，因此连续层可以折叠合并
4. 训练阶段的末尾需要一层 Sigmoid 激活函数以获得合理的误差，推理阶段可以删除这一层，因为 Sigmoid 是单调增的，同时 CNN 的输出值是向量的最大值索引

CryptoDL

[HTG17] 提出了 CryptoDL 模型，他们仅关注推理，模型是明文训练的。他们使用 HElib 库中的 BGV 方案。在 MNIST 数据集上，预测精度为 $99.52\%$，吞吐率是每小时 164000 次预测，单次预测的延迟是 320 秒。

多项式近似

在 CNN 的所有运算中，最关键的就是激活函数，同时激活函数在 FHE 下的计算也是最复杂的。[HTG17] 使用低次多项式去近似 Sigmoid/Tanh/ReLU 激活函数。

Stone–Weierstrass 定理：令 $X$ 是一个非空的紧空间，简记 $C(X)$ 是其上的所有连续实值函数的族。令 $A$ 是由一些多项式组成的集合，它在加法、乘法、数乘下封闭，且包含所有的常数函数。我们说某个 $f\in C(X)$ 可以被 $A$ 近似，如果对于任意的 $ϵ>0$ 总存在 $p\in A$ 使得 $|f(x)-p(x)|<ϵ,\forall x\in X$。那么，$C(X)$ 中的任意元素都可以被 $A$ 近似 $⟺$ 对于任意的 $x\ne y\in X$ 总存在 $p\in A$ 使得 $p(x)\ne p(y)$。

只不过这个定理是非构造性的。我们令 $\mu$ 是集合 $X$ 上的度量，那么可以定义函数空间 $C(f)$ 的内积 $⟨f,g⟩:={\int }_{X}fg\text{ d}\mu$。使用 $\text{ d}\mu =\text{ d}x$ 以及 $[-1,1]$，利用 GSO 可以获得空间的一组生成多项式，称为 Legendre 多项式。使用 $\text{ d}\mu =\frac{\text{ d}x}{\sqrt{1-x^2}}$ 以及 $[-1,1]$，利用 GSO 可以获得空间的一组生成多项式，称为 Chebyshev 多项式。前者用于泰勒级数，后者用于多项式插值。

由于 Sigmoid 函数 $\sigma (x)=\frac{1}{1+e^{-x}}$ 以及 Tanh 函数 $2\sigma (x)-1$ 都是无限可导的（infinitely derivative），因此可以直接用 Chebyshev 插值算法去近似。

而 ReLU 函数 $\max (0,x)$ 的导数是阶跃函数，原点附近不存在二阶导数，因此近似效率不好。[HTG17] 尝试了数值分析、泰勒级数、标准切比雪夫插值及其变体，表现的都不好。他们认为在 CNN 中的激活函数的导数是十分重要的，这影响错误的评估以及权重的更新。因此，他们使用低次多项式去拟合阶跃函数，然后把积分结果作为对 ReLU 的近似。

网络结构

[HTG17] 采用度数为 2 - 3 的低次多项式替换原始的激活函数，分别训练了浅层网络和深层网络，前者精度 $98.52\%$，后者精度 $99.52\%$

Others

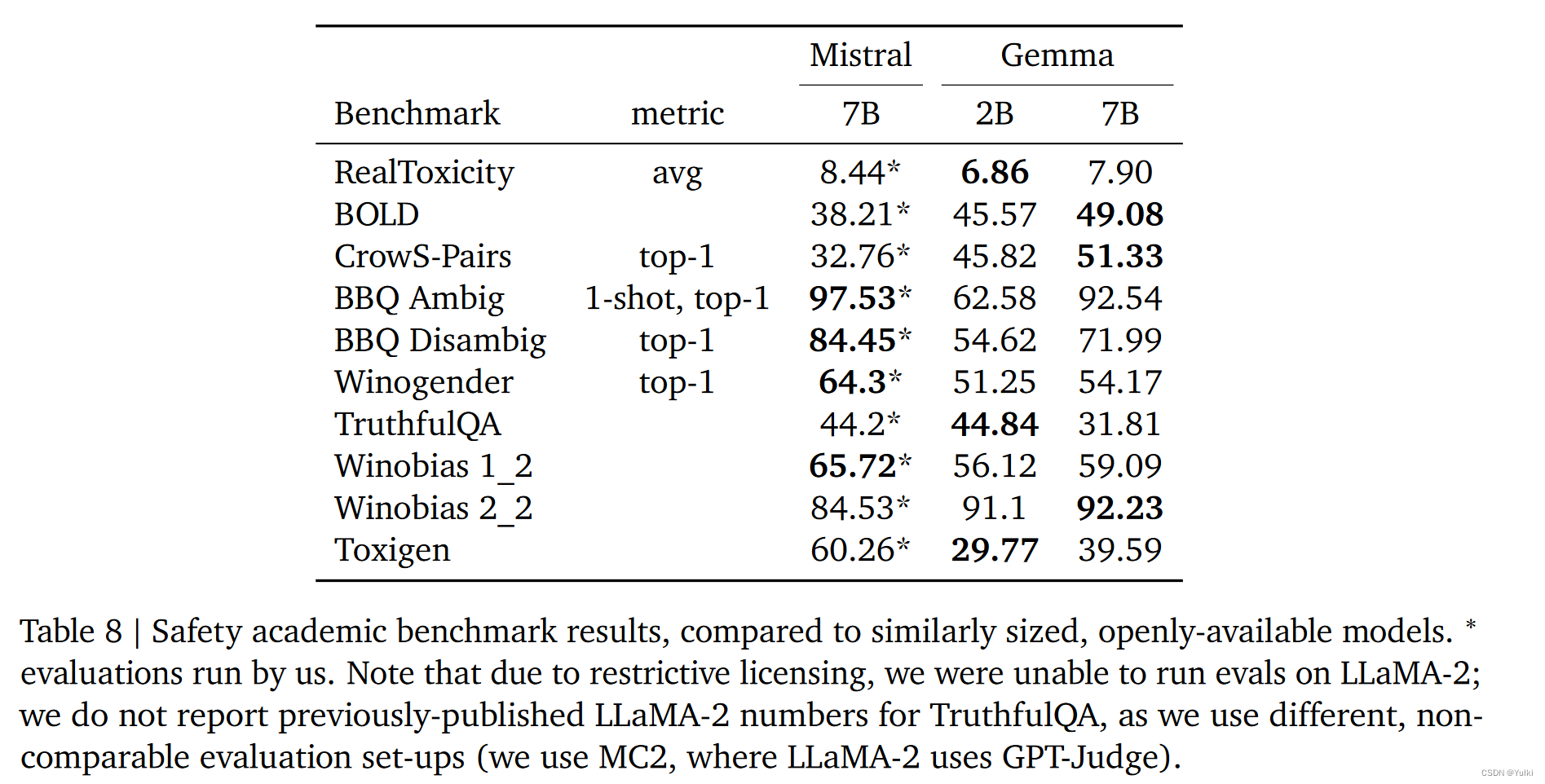
上述的工作都是简单的非标准模型（网络深度很浅，激活函数被替换，数据集简单），[LKL+22] 第一次给出了标准的深度学习模型（ResNet-20）的同态预测。他们使用 RNS-CKKS 方案，并在 SEAL 库中实现了 Bootstrapping 算法。模型是在明文下训练的标准 ResNet-20，在推理的时候对 Softmax 激活函数做高精度的近似。