思路

难点1
如何理解特殊字符 ’ * ’ 的作用？
如何正确的利用特殊字符 ’ . ’ 和 ’ * ’ ？

'*' 匹配零个或多个前面的那一个元素
"a*" 可表示的字符为不同数目的 'a'，包括：
""（0 个 'a'）
"a"（1 个 'a'）
"aa"（2 个 'a'）
"aaa"（3 个 'a'）

难点2
正则表达式匹配:一种在文本中查找特定模式的方法。
这道题的正则匹配规则主要是 ’ * '、 ’ . ’ 这两个特殊字符的使用。

如何利用现有数据结构 构造这个问题？
按照规则，（有顺序）从左到右来匹配一个字符串。
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

如果不考虑这两个特殊字符，我们可以用二维数组来动态的表示两个字符串是否匹配。只有前面的数组匹配上，后面的数组才可以继续匹配。

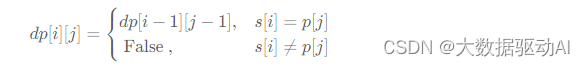
但现在要考虑 ’ * '、 ’ . ’ 这两个特殊字符。
p[j]= ‘.’，则 p[j]一定可以与 s[i]匹配成功，此时有dp[i][j]=dp[i−1][j−1]
p[j]= ‘*’，则表示可对 p[j]的前一个字符 p[j−1]匹配（或理解为复制）任意次（包括 0 次）。

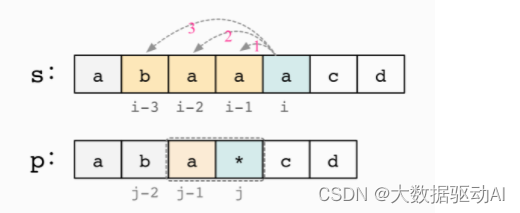
匹配0次，意味着 p[j−1]和 p[j]不起作用，
相当于在 p 中删去了 p[j−1]和 p[j]，
此时有：dp[i][j]=dp[i][j−2]

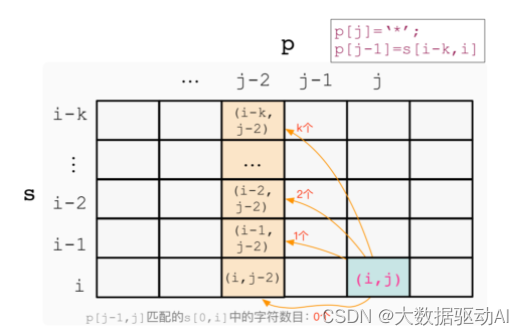
匹配 1次，意味着 p[j−1]和 p[j]组成了 1 个’a’，若 s[i−1+1, …, i]=p[j−1]，
则 dp[i][j]可由 dp[i−1][j−2]转移而来，
此时有：dp[i][j]=dp[i−1][j−2],&s[i−1+1, …, i]=p[j−1]

匹配 k 次，意味着 p[j−1]和 p[j]组成了 k 个’a’，若 s[i−k+1, …, i]=p[j−1]，
则 dp[i][j]可由 dp[i−k][j−2]转移而来，
此时有：dp[i][j]=dp[i−k][j−2],&s[i−k+1, …, i]=p[j−1]

难点3
状态转移的优化
总的来看，当 p[j]= '’ 时，对于匹配 0∼k次，我们有：

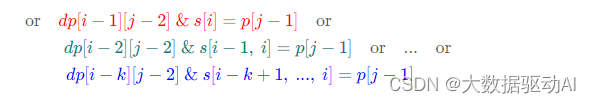
同时，对于 dp[i−1][j]我们有：

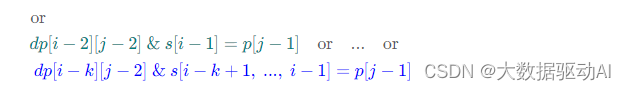
观察发现，（2）式与（1）式中的后 k 项刚好相差了一个条件 s[i]=p[j−1]，将（2）式代入（1）式可得简化后的「状态转移方程」为：
p[j]= ''时，简化后对应的状态更新过程如下图所示：

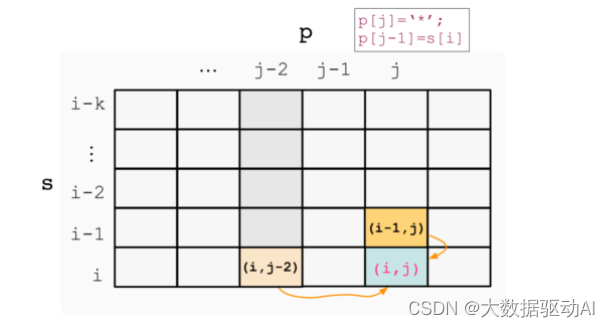
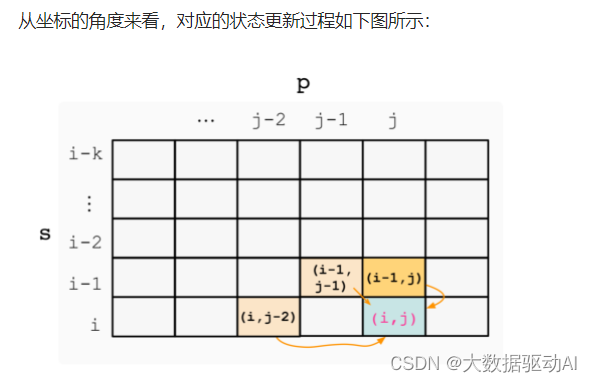
记 s 的长度为 m，p的长度为 n 。为便于状态更新，减少对边界的判断，初始二维 dpdpdp 数组维度为 (m+1)×(n+1)，其中第一行和第一列的状态分别表示字符串 s 和 p 为空时的情况。

显然，dp[0][0]=True。对于其他 dp[0][j]，当 p[j]≠p[j]='‘时，s[0,…,j]无法与空字符匹配，因此有 dp[0][j]=False；而当 p[j]=p[j]=p[j]=’'时，则有 dp[0][j]=dp[0][j−2]。

python

class Solution:
    def isMatch(self, s: str, p: str) -> bool:

        m, n = len(s), len(p)
        dp = [[False] * (n+1) for _ in range(m+1)]
        
        # 初始化
        dp[0][0] = True
        for j in range(1, n+1):
            if p[j-1] == '*':
                dp[0][j] = dp[0][j-2]

        # 状态更新
        for i in range(1, m+1):
            for j in range(1, n+1):
                if s[i-1] == p[j-1] or p[j-1] == '.':
                    dp[i][j] = dp[i-1][j-1]
                elif p[j-1] == '*':     # 【题目保证'*'号不会是第一个字符，所以此处有j>=2】
                    if s[i-1] != p[j-2] and p[j-2] != '.':
                        dp[i][j] = dp[i][j-2]
                    else:
                        dp[i][j] = dp[i][j-2] | dp[i-1][j]
        
        return dp[m][n]