Gradient Descent and Newton Descent

一、下降法【Descent】

首先介绍什么是下降法【Descent Methods】，下降法就是求解无约束优化问题的一种基本方法。无约束最小化问题是指：

无约束最小化问题满足以下的条件：

最小化函数 $f (x)$
$f (x)$ 是凸函数，二阶连续可导
并且 $f (x)$ 的最优值是能够求解的

下降法通俗的理解就是从初始 $\bold{x}(0)$ 开始，然后指定迭代的方向 $\Delta{x}$ ，指定每次迭代的步长 $t$ ，经过迭代（如果没有达到迭代终止条件，则迭代完指定次数），经过这样迭代的搜索最终寻找到最终值。
其中 $x^{(k+1)}=x^{(k)}+t^{(k)}\Delta{x^{(k)}}$ 是每次的参数更新公式， $x^{(k+1)}$ 代表第 $k + 1$ 次的参数， $t^{(k)}$ 是第 $k$ 次的迭代步长， $\Delta{x^{(k)}}$ 是第 $k$ 次的迭代方向。

二、梯度下降法【Gradient Descent】

接下来，介绍什么是梯度下降法【Gradient Descent】

梯度下降法只是在下降法的基础上，将下降的方向 $\Delta{x}$ 修改为 $-\nabla{f(x)}$ ，同时增加了终止条件 $\Vert\nabla{f(x)}\Vert_2\le\epsilon$ ，其中 $\epsilon$ 是容忍限度，是一个极小值。

三、牛顿下降法【Newton Descent】

然后介绍什么是牛顿下降法【Newton Descent】

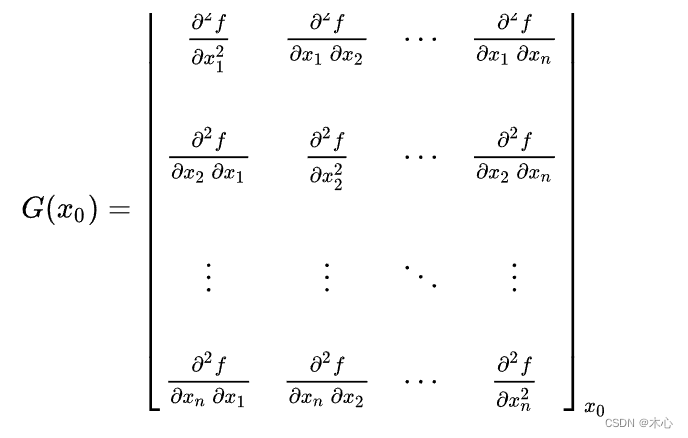
牛顿下降法也是在下降法的基础上进行了更改，将下降的方向更改为 $\Delta{x}=\Delta{x_{nt}}$ ， $\Delta{x_{nt}}:=-\nabla^2f(x)^{-1}\nabla{f(x)}$ ，且增加了终止条件 $\lambda^2:=\nabla{f(x)^T}\nabla^2f(x)^{-1}\nabla{f(x)}\le\epsilon$ ，其中 $\epsilon$ 是容忍限度，是一个极小值。其中， $\nabla^2f(x)$ 是Hessian矩阵，具体的求法如下

四、示例Example

考虑以下的凸优化问题：
$\underset{x_1,x_2}{min}\quad{\frac{1}{2}(x_1^2+3x_2^2)}$

分别利用梯度下降法和牛顿下降法进行求解

import numpy as np
import matplotlib.pyplot as plt

fig1 = plt.figure()
ax3 = plt.axes(projection='3d')

def func(x1,x2):
    return (np.power(x1,2) + 3*np.power(x2,2)) / 2
    
#------------------------------Gradient Descent------------------------------
# 用近似导数来代替导数,方便数值计算,且更具一般性
def df_x1(f, x1, x2, delta=1e-4):
    return (f(x1+delta,x2) - f(x1-delta,x2)) / (2*delta)
def df_x2(f, x1, x2, delta=1e-4):
    return (f(x1,x2+delta) - f(x1,x2-delta)) / (2*delta)

# 定义三维绘制点坐标
X1 = np.arange(-5,5,0.1)
X2 = np.arange(-5,5,0.1)
X1s, X2s = np.meshgrid(X1,X2)
Ys = func(X1s, X2s)
# 绘图渲染和显示
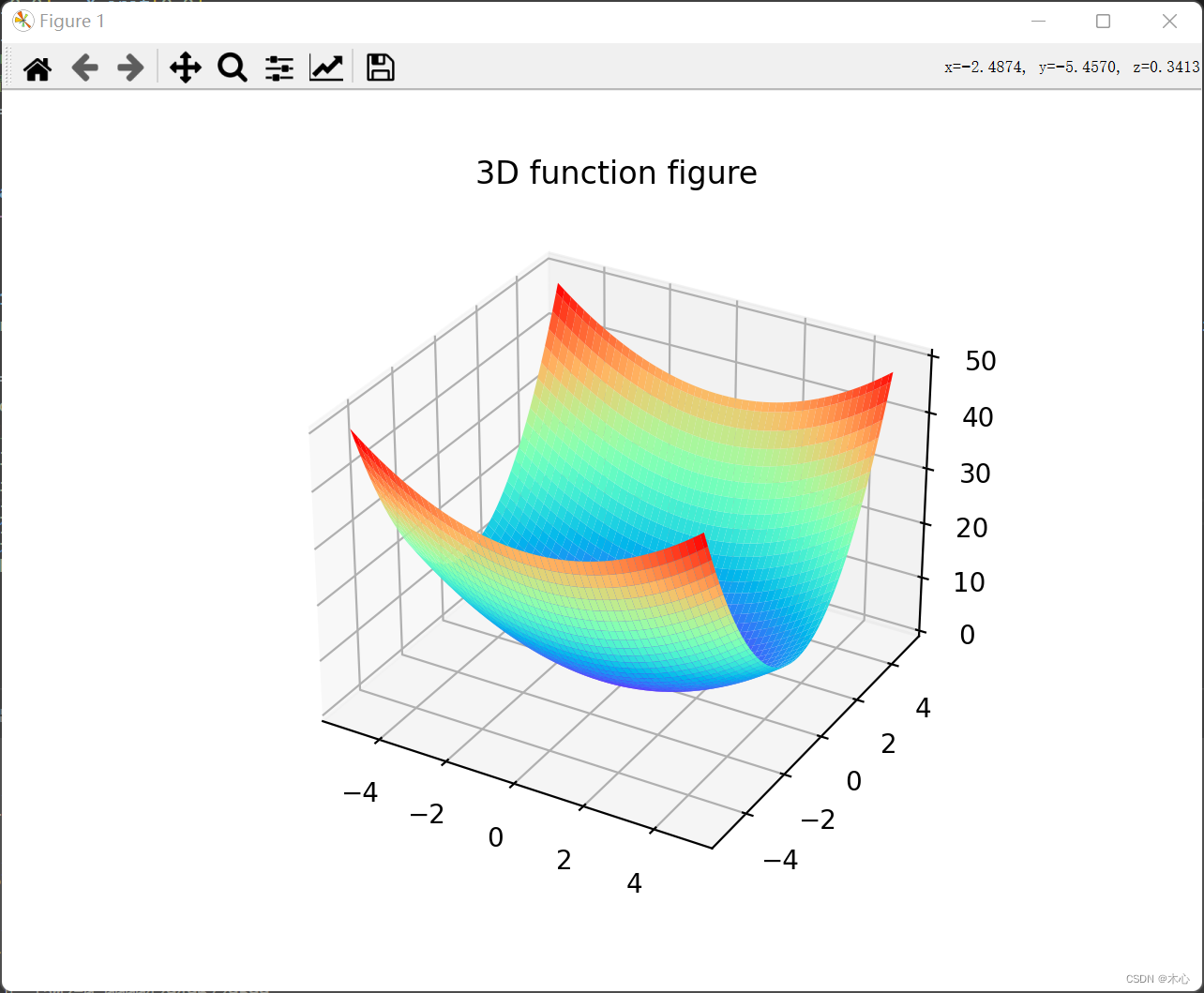
ax3.plot_surface(X1s,X2s,Ys, cmap='rainbow')
plt.title("3D function figure")
plt.show()

# 设置学习率和循环次数
alpha = 0.1
max_loop = 50
# 初始化x1=2,x2=2
X_init = np.matrix([2,2])

# 开辟存储空间
x1 = np.zeros([1,51])
x2 = np.zeros([1,51])
x1[0,0] = X_init[0,0]
x2[0,0] = X_init[0,1]
# Gradient descent迭代循环
Eps = 1e-4
for i in range(max_loop):
    # 迭代停止条件:梯度的二范数大于Eps
    df_l2 = np.sqrt(np.power(df_x1(func, x1[0,i], x2[0,i]),2) + np.power(df_x2(func, x1[0,i], x2[0,i]),2))
    if df_l2 <= Eps:
        print("第%d轮,迭代停止,df_l2=%.16f\n" %(i+1,df_l2))
        break
    x1[0,i+1] = x1[0,i] - alpha * df_x1(func, x1[0,i], x2[0,i])
    x2[0,i+1] = x2[0,i] - alpha * df_x2(func, x1[0,i], x2[0,i])
    print("当前是第%d轮,x1=%.16f,x2=%.16f,f(x1,x2)=%.16f\n,df_l2=%.16f\n" %(i+1,x1[0,i+1],x2[0,i+1],func(x1[0,i+1], x2[0,i+1]),df_l2))

# 绘制等高线图
fig2 = plt.figure()
plt.contour(X1s,X2s,Ys,colors='k')
# 绘制梯度下降曲线
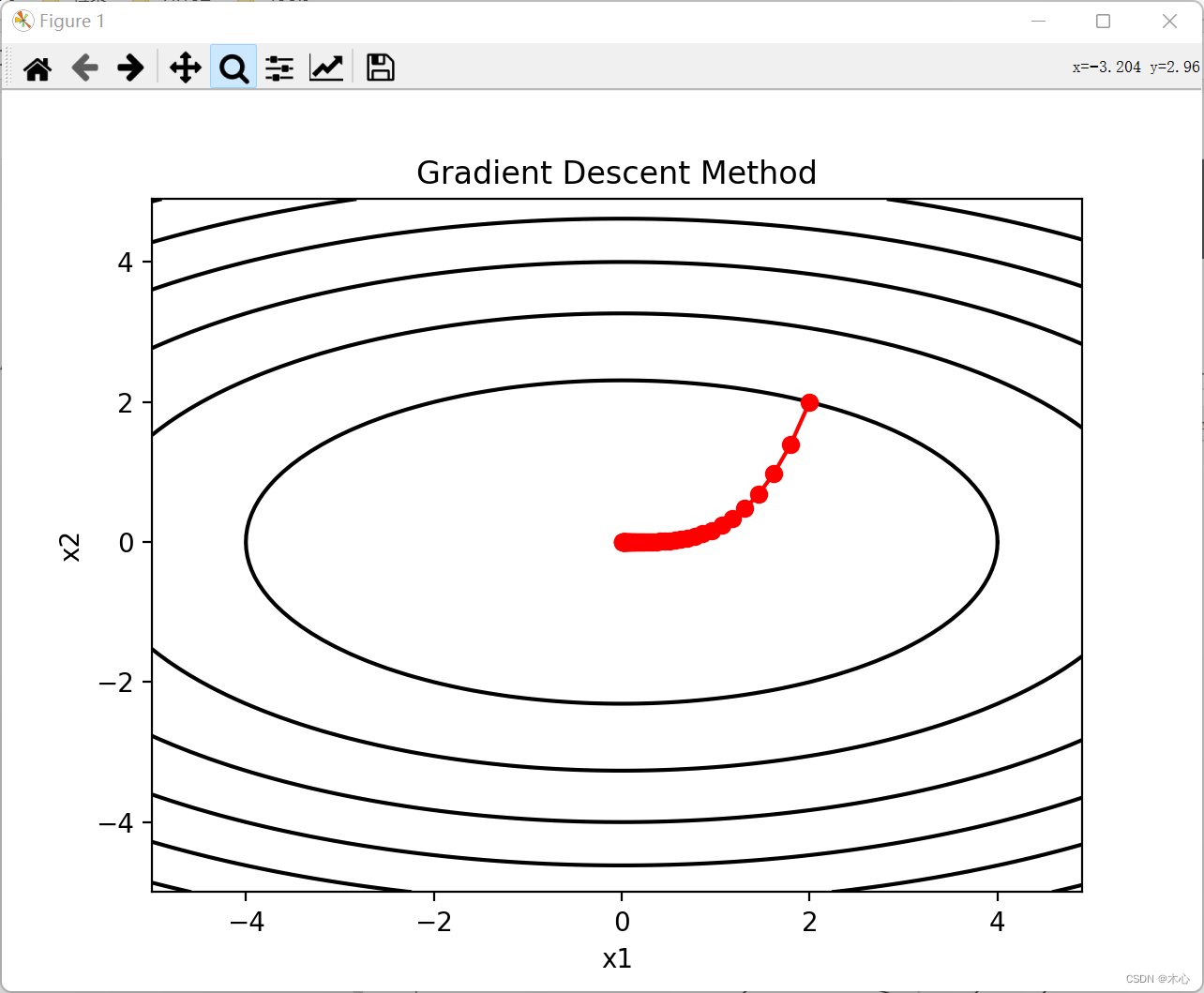
plt.plot(x1[0],x2[0],'-ro')
plt.title("Gradient Descent Method")
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()



#------------------------------Newton Descent------------------------------
def delta_f(f, x1, x2, d=1e-4):
    dx1 = (f(x1+d,x2) - f(x1-d,x2)) / (2*d)
    dx2 = (f(x1,x2+d) - f(x1,x2-d)) / (2*d)
    return np.matrix([[dx1],[dx2]])
def hessian_f(x1, x2):
    # 只争对f = 1/2(x1^2+3*x2^2)
    h11 = 1
    h12 = 0
    h13 = 0
    h14 = 3
    return np.matrix([[1,0], [0,3]])

def newton_step(f, x1, x2):
    delta = delta_f(f, x1, x2)
    H = hessian_f(x1, x2)
    return np.dot(H.I,delta)

def lambda2(f,x1,x2):
    delta = delta_f(f, x1, x2)
    H = hessian_f(x1, x2)
    return np.dot(np.dot(delta.T, H.I), delta)

a = newton_step(func, 1, 1)
b = lambda2(func,1,1)
print(a, a.shape)
print(b, b.shape)

# 开辟空间并初始化
x12 = np.zeros([51,2,1])
x12[0,0,0] = X_init[0,0]
x12[0,1,0] = X_init[0,1]
# print(x12, x12.shape)
# 设置学习率
beta = 0.6

for i in range(max_loop):
    lam2 = lambda2(func,x12[i,0,0],x12[i,1,0])
    if lam2 <= Eps:
        print("第%d轮,迭代停止,lam2=%.16f\n" %(i+1,lam2))
        break
    x12[i+1] = x12[i] - beta*newton_step(func,x12[i,0,0],x12[i,1,0])
    print("当前是第%d轮,x1=%.16f,x2=%.16f,f(x1,x2)=%.16f\n,lam2=%.16f\n" %(i+1, x12[i+1,0,0], x12[i+1,1,0], func(x12[i+1,0,0], x12[i+1,1,0]),lam2))

fig3 = plt.figure()
plt.contour(X1s,X2s,Ys,colors='k')
# 绘制梯度下降曲线
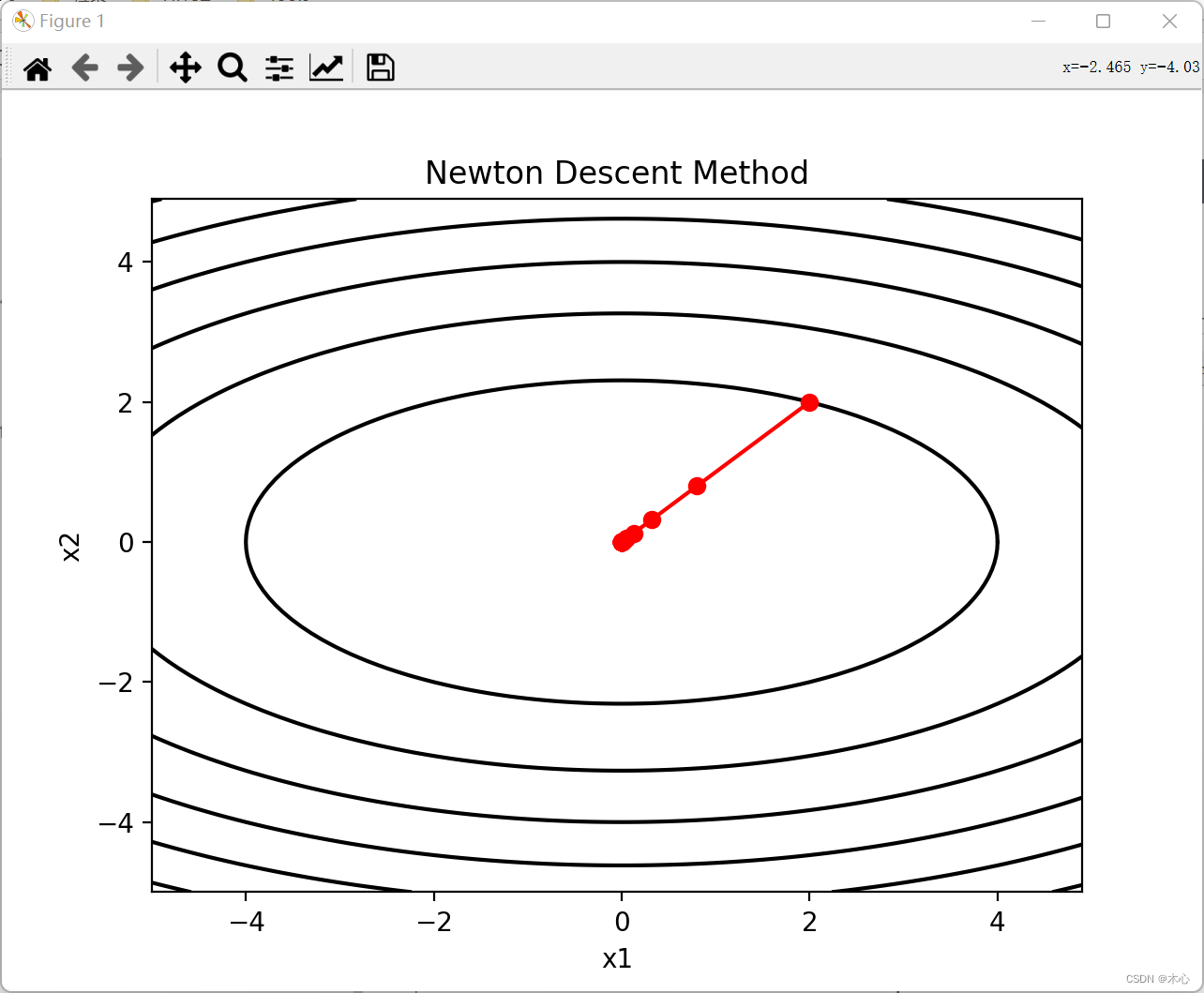
plt.plot(x12[:,0,0],x12[:,1,0],'-ro')
plt.title("Newton Descent Method")
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()