1.GAN
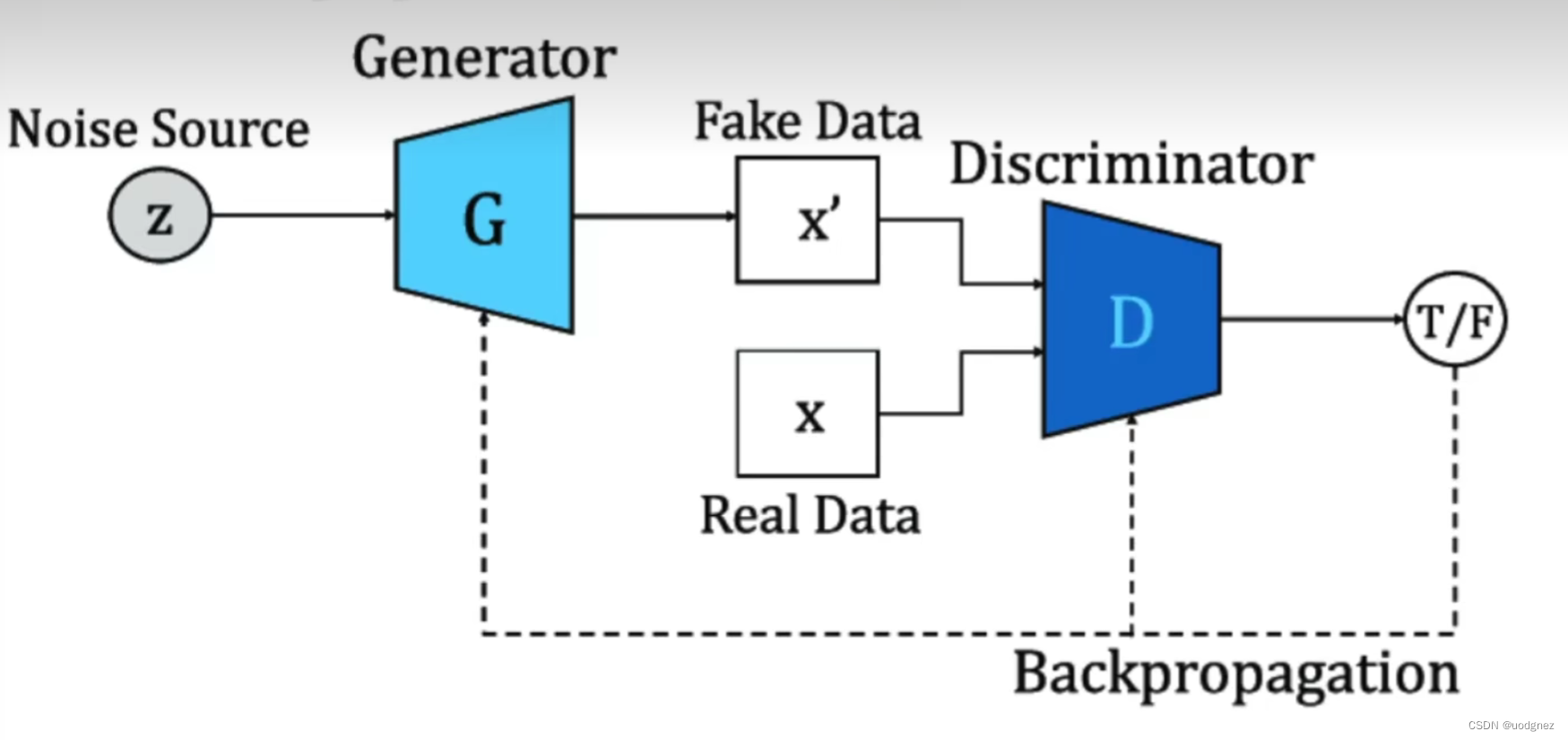
在训练过程中,生成器和判别器的目标是相矛盾的,并且这种矛盾可以体现在判别器的判断准确性上。生成器的目标是生成尽量真实的数据,最好能够以假乱真、让判别器判断不出来,因此生成器的学习目标是让判别器上的判断准确性越来越低;相反,判别器的目标是尽量判别出真伪,因此判别器的学习目标是让自己的判别准确性越来越高。
当生成器生成的数据越来越真时,判别器为维持住自己的准确性,就必须向辨别能力越来越强的方向迭代。当判别器越来越强大时,生成器为了降低判别器的判断准确性,就必须生成越来越真的数据。在这个奇妙的关系中,判别器判断的准确性由GAN论文中定义的特殊交叉熵 V V V来衡量,判别器与生成器共同影响交叉熵 V V V,同时训练、相互内卷,对该交叉熵的控制时此消彼长的,这是真正的零和博弈。
2. 特殊交叉熵 V V V
在生成器与判别器的内卷关系中,GAN的特殊交叉熵公式如下:
V
(
D
,
G
)
=
1
m
∑
i
=
1
m
[
log
D
(
x
i
)
+
log
(
1
−
D
(
G
(
z
i
)
)
)
]
V(D,G)=\frac1m\sum_{i=1}^{m}[\log D(x_i) +\log(1-D(G(z_i)))]
V(D,G)=m1i=1∑m[logD(xi)+log(1−D(G(zi)))]
其中,字母
V
V
V是原始GAN论文中指定用来表示该交叉熵的字母,对数
log
\log
log的底数为自然底数
e
e
e,
m
m
m表示共有
m
m
m个样本,因此以上表达式是全部样本交叉的均值表达式。
除此之外,
x
i
x_i
xi表示任意真实数据,
z
i
z_i
zi与真实数据相同结构的任意随机数据,
G
(
z
i
)
G(z_i)
G(zi)表示在生成器中基于
z
i
z_i
zi生成的假数据,而
D
(
x
i
)
D(x_i)
D(xi)表示判别器在真实数据
x
i
x_i
xi上判断出的结果,
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))表示判别器在假数据
G
(
z
i
)
G(z_i)
G(zi)上判断出的结果,其中
D
(
x
i
)
D(x_i)
D(xi)与
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))都是样本为“真”的概率,即标签为
1
1
1的概率。
在原始论文中,这一交叉熵被认为是一种“损失”,但它有两个特殊之处:
- 不同于二分类交叉熵等常见的损失函数,损失 V V V上不存在最小值,反而存在最大值。具体来看, D ( x i ) D(x_i) D(xi)与 D ( G ( z i ) ) D(G(z_i)) D(G(zi))都是概率,因此这两个值的范围都在 ( 0 , 1 ) (0,1) (0,1)之间。对于底数为 e e e的对数函数来说,在定义域为 ( 0 , 1 ) (0,1) (0,1)之间意味着函数的值为 ( − ∞ , 0 ) (-\infty,0) (−∞,0)。因此理论上来说,损失 V V V的值域也在 ( − ∞ , 0 ) (-\infty,0) (−∞,0)。
- 损失 V V V在判别器的判别能力最强时达到最大值,这就是说判别器判断得越准确时,损失反而越大,这违背我们对普通二分类网络中的损失函数的期待。但我们从判别器和生成器角度分别来看待公式 V V V,则可以很快理解这一点。
不难发现,在
V
V
V的表达式中,两部分对数都与判别器
D
D
D有关,而只有后半部分的对数与生成器
G
G
G有关。因此我们可以按如下方式分割损失函数:
对判别器:
L
o
s
s
D
=
1
m
∑
i
=
1
m
[
log
D
(
x
i
)
+
log
(
1
−
D
(
G
(
z
i
)
)
)
]
Loss_D=\frac1m\sum_{i=1}^m[\log D(x_i) +\log(1-D(G(z_i)))]
LossD=m1i=1∑m[logD(xi)+log(1−D(G(zi)))]
从判别器的角度来看,由于判别器希望自己尽量能够判断正确,而输出概率又是“数据为真”的概率,所以最佳情况就是所有的真实样本上的输出
D
(
x
i
)
D(x_i)
D(xi)都无比接近
1
1
1,而所有的假样本上的输出
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))都无比接近
0
0
0。因此对判别器来说,最佳损失值是:
L
o
s
s
D
=
1
m
∑
i
=
1
m
[
log
D
(
x
i
)
+
log
(
1
−
D
(
G
(
z
i
)
)
)
]
=
1
m
∑
i
=
1
m
[
log
1
+
log
(
1
−
0
)
]
=
0
Loss_D=\frac1m\sum_{i=1}^m[\log D(x_i) +\log(1-D(G(z_i)))]= \frac1m\sum_{i=1}^m[\log 1+\log (1-0)]= 0
LossD=m1i=1∑m[logD(xi)+log(1−D(G(zi)))]=m1i=1∑m[log1+log(1−0)]=0
这说明判别器希望以上损失
L
o
s
s
D
Loss_D
LossD越大越好,且最大值理论上可达
0
0
0,且判别器追求大
L
o
s
s
D
Loss_D
LossD的本质是令
D
(
x
)
D(x)
D(x)接近
1
1
1,令
D
(
G
(
z
)
)
D(G(z))
D(G(z))接近
0
0
0。不难发现,对判别器而言,
V
V
V更像是一个存在上限的积极的指标(比如准确率)。
而从生成器的角度来看,生成器无法影响
D
(
x
i
)
D(x_i)
D(xi),只能影响
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi)),因此只有损失的后半段与生成器相关。因此对生成器:
L
o
s
s
G
=
1
m
∑
i
=
1
m
[
常数
+
log
(
1
−
D
(
G
(
z
i
)
)
)
]
Loss_G=\frac1m\sum_{i=1}^m[常数+\log(1-D(G(z_i)))]
LossG=m1i=1∑m[常数+log(1−D(G(zi)))]
生成器的目标是令输出的数据越真越好,最好让判别器完全判断不出,因此生成器希望
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))越接近
1
1
1越好。因此对生成器来说,最佳损失是(去掉常数项):
L
o
s
s
G
=
1
m
∑
i
=
1
m
log
(
1
−
D
(
G
(
z
i
)
)
)
=
log
(
1
−
1
)
=
−
∞
Loss_G=\frac1m\sum_{i=1}^m\log(1-D(G(z_i)))= \log(1-1)= -\infty
LossG=m1i=1∑mlog(1−D(G(zi)))=log(1−1)=−∞
这说明生成器希望以上损失
L
o
s
s
G
Loss_G
LossG越小越好,且最小理论值可达负无穷,且生成器追求小
L
o
s
s
G
Loss_G
LossG的本质是令
D
(
G
(
z
)
)
D(G(z))
D(G(z))接近
1
1
1。对生成器而言,
V
V
V更像是一个损失,即算法表现越好,该指标的值越低。从整个生成对抗网络的角度来看,我们(使用者)的目标与生成器的目标相一致,因此对我们而言,
V
V
V被定义为损失,它应该越低越好。
在原始论文当中,该损失
V
V
V被表示为如下形式:
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
P
d
a
t
a
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
P
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\min \limits_G \max \limits_D V(D, G)=\mathbb{E}_{x \sim{P_{data}} (x)} [\log D(x)] + \mathbb{E}_{z \sim{P _{z}}(z)}[\log (1 - D(G(z)))]
GminDmaxV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼Pz(z)[log(1−D(G(z)))]
即先从判别器的角度令损失最大化,又从生成器的角度令损失最小化,即可让判别器和生成器在共享损失的情况下实现对抗。其中
E
\mathbb{E}
E表示期望,第一个期望
E
x
∼
P
d
a
t
a
(
x
)
[
log
D
(
x
)
]
\mathbb{E}_{x \sim{P_{data}} (x)} [\log D(x)]
Ex∼Pdata(x)[logD(x)]是所有
x
x
x都是真实数据时
log
D
(
x
)
\log D(x)
logD(x)的期望;第二个期望
E
z
∼
P
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\mathbb{E}_{z \sim{P _{z}}(z)}[\log (1 - D(G(z)))]
Ez∼Pz(z)[log(1−D(G(z)))]是所有数据都是生成数据时
log
(
1
−
D
(
G
(
z
)
)
)
\log (1 - D(G(z)))
log(1−D(G(z)))的期望。当真实数据、生成数据的样本点固定时,期望就等于均值。
如此,通过共享以上损失函数,生成器与判别器实现了在训练过程中互相对抗,
min
G
max
D
V
(
D
,
G
)
\min \limits_G \max \limits_D V(D, G)
GminDmaxV(D,G)的本质就是最小化
L
o
s
s
G
Loss_G
LossG的同时最大化
L
o
s
s
D
Loss_D
LossD。并且,在最开始训练时,由于生成器生成的数据与真实数据差异很大,因此
D
(
x
i
)
D(x_i)
D(xi)应该接近
1
1
1,
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))应该接近
0
0
0。理论上来说,只要训练顺利,最终
D
(
x
i
)
D(x_i)
D(xi)和
D
(
G
(
z
i
)
)
D(G(z_i))
D(G(zi))都应该非常接近
0.5
0.5
0.5,但实际上这样的情况并不常见。
B站up:菜菜