一、灰色关联分析简介
一般的抽象系统,如社会系统、经济系统、农业系统、生态系统、教育系统等都包含有许多种因素,多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中,哪些是主要因素,哪些是次要因素;哪些因素对系统发展影响大,哪些因素对系统发展影响小;哪些因素对系统发展起推动作用需强化发展,哪些因素对系统发展起阻碍作用需加以抑制......这些都是系统分析中人们普遍关心的问题。例如,粮食生产系统,人们希望提高粮食总产量,而影响粮食总产量的因素是多方面的,有播种面积以及水利、化肥、土壤、种子、劳力、气候、耕作技术和政策环境等。为了实现少投人多产出,并取得良好的经济效益、社会效益和生态效益,就必须进行系统分析。
数理统计中的回归分析、方差分析、主成分分析等都是用来进行系统分析的方法。这些方法都有下述不足之处:
- 要求有大量数据,数据量少就难以找出统计规律
- 要求样本服从某个典型的概率分布,要求各因素数据与系统特征数据之间呈线性关系且各因素之间彼此无关,这种要求往往难以满足
- 计算量大,一般要靠计算机帮助
- 可能出现量化结果与定性分析结果不符的现象,导致系统的关系和规律遭到歪曲和颠倒
尤其是我国统计数据十分有限,而且现有数据灰度较大,再加上人为的原因,许多数据都出现几次大起大落,没有典型的分布规律。因此,采用数理统计方法往往难以奏效。
灰色关联分析方法弥补了采用数理统计方法作系统分析所导致的缺憾。它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。
------参考教材《灰色系统理论及其应用》
二、适用赛题
系统分析,如上面所述,系统分析问题可使用。
但是,也可在综合评价类问题中使用灰色关联分析。
三、模型流程
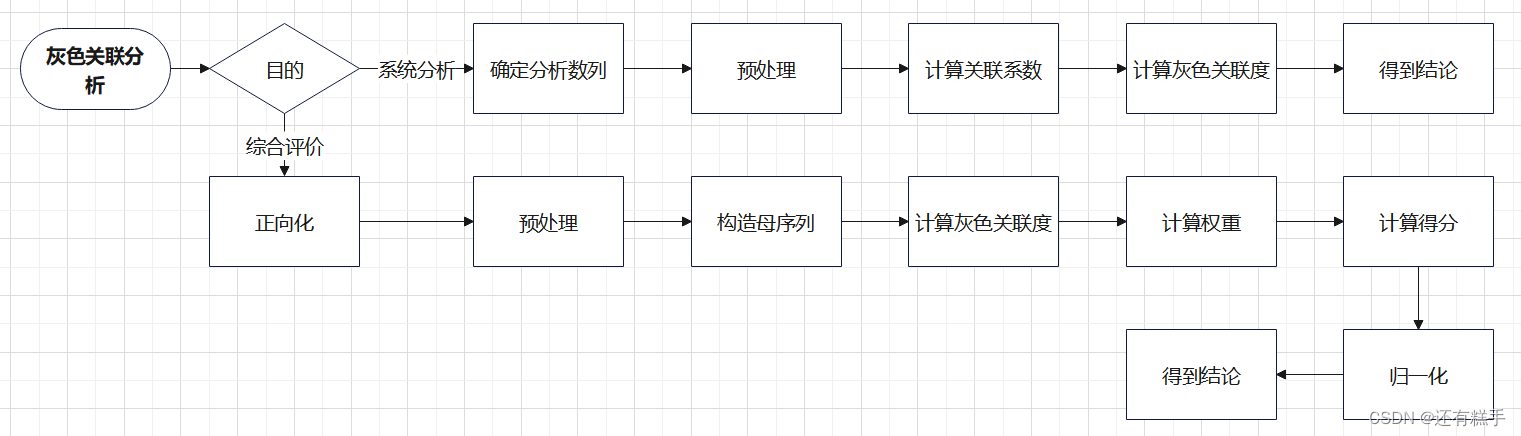
四、流程分析
这里分为两类运用,分别分析。
1.系统分析
①确定分析数列
有两种数列,母序列和子序列。
母序列(又称参考数列、母指标)
- 能反映系统行为特征的数据序列
- 类似于因变量Y,此处记为X0
子序列(又称比较序列、子指标)
- 影响系统行为的因素组成的数据序列
- 类似于自变量X,此处记为(X1, X2, .., Xm)
确定好题目中的两种序列。
②预处理
预处理有两个目的
- 去量纲
- 缩小变量范围,简化计算
这里的预处理十分简单:先求出每个指标的均值,再用该指标中的每个元素都除以其均值。
③计算关联系数
首先要找到a(两极最小差)和b(两极最大差),这里定义
- X0 = (X0(1), X0(2), ..., X0(n))的转置,这是母序列
- X1 = (X1(1), X1(2), ..., X1(n))的转置,这是子序列
- ......
- Xm = (Xm(1), Xm(2), ..., Xm(n))的转置,这是子序列
而a = min min|X0(k) - Xi(k)|,b = max max|X0(k) - Xi(k)|
定义γ(X0(k), Xi(k)) = (a+ρb) / (|X0(k) - Xi(k)| + ρb)
ρ是分辨系数,一般取0.5;i = 1, 2, ..., m,k = 1, 2, ..., n
这样就得到了关联系数矩阵。
④计算灰色关联度
定义γ(X0, Xi) = 1/n * Σγ(X0(k), Xi(k))为X0和Xi的灰色关联度。其实就是每个指标求平均值。
k = 1, 2, ..., n
⑤得到结论
通过比较三个子序列和母序列的关联度可以得到结论(灰色关联度越大,影响越大)。
2.综合评价
①正向化
对指标进行正向化,正向化操作在TOPSIS法中已讲解,这里不做赘述。
②预处理
预处理操作和系统分析预处理操作相同。
③构造母序列
将预处理后的矩阵每一行取出最大值构成母序列(虚构的)。
④计算灰色关联度
操作和系统分析相同。
⑤计算权重
每个指标的权重是这个指标灰色关联度除以所有指标灰色关联度之和。
⑥计算得分
每个对象用对应指标的数值乘以相应指标的权重之和就是此对象的得分。
⑦归一化
用这个对象得分除以所有对象的得分就得到归一化后的得分。
⑧得到结论
根据得分进行评价。
五、补充
1.什么时候用标准化回归,什么时候用灰色关联分析?
当样本个数n较大时,一般用标准化回归;当样本个数n较小时,才使用灰色关联分析。
2.如果母序列中有多个指标,应该怎么分析?例如Y1和Y2是母序列,X1、X2、...、Xm是子序列
那么我们首先计算Y1和X1、X2、...、Xm的灰色关联度进行分析;在计算Y2和X1、X2、...、Xm的灰色关联度进行分析。
------参考回答:清风