AtCoder Beginner Contest 284
- A - Sequence of Strings
- 1、问题
- 2、代码
- B - Multi Test Cases
- 1、问题
- 2、代码
- C - Count Connected Components
- 1、问题:
- 2、思路:——并查集、DFS
- 3、代码
- 方法1:并查集
- 方法2:DFS
- D - Happy New Year 2023
- 1、问题
- 2、思路——算数基本定理、欧拉筛
- 方法一:欧拉筛
- 方法二:算数基本定理
- 3、代码
- E - Sequence of Strings
- 1、问题
- 2、思路——DFS
- 3、代码
- 链式前向星版邻接表
- vector版邻接表
(AB题很简单,略过)
传送门:AtCoder Beginner Contest 284
A - Sequence of Strings
1、问题
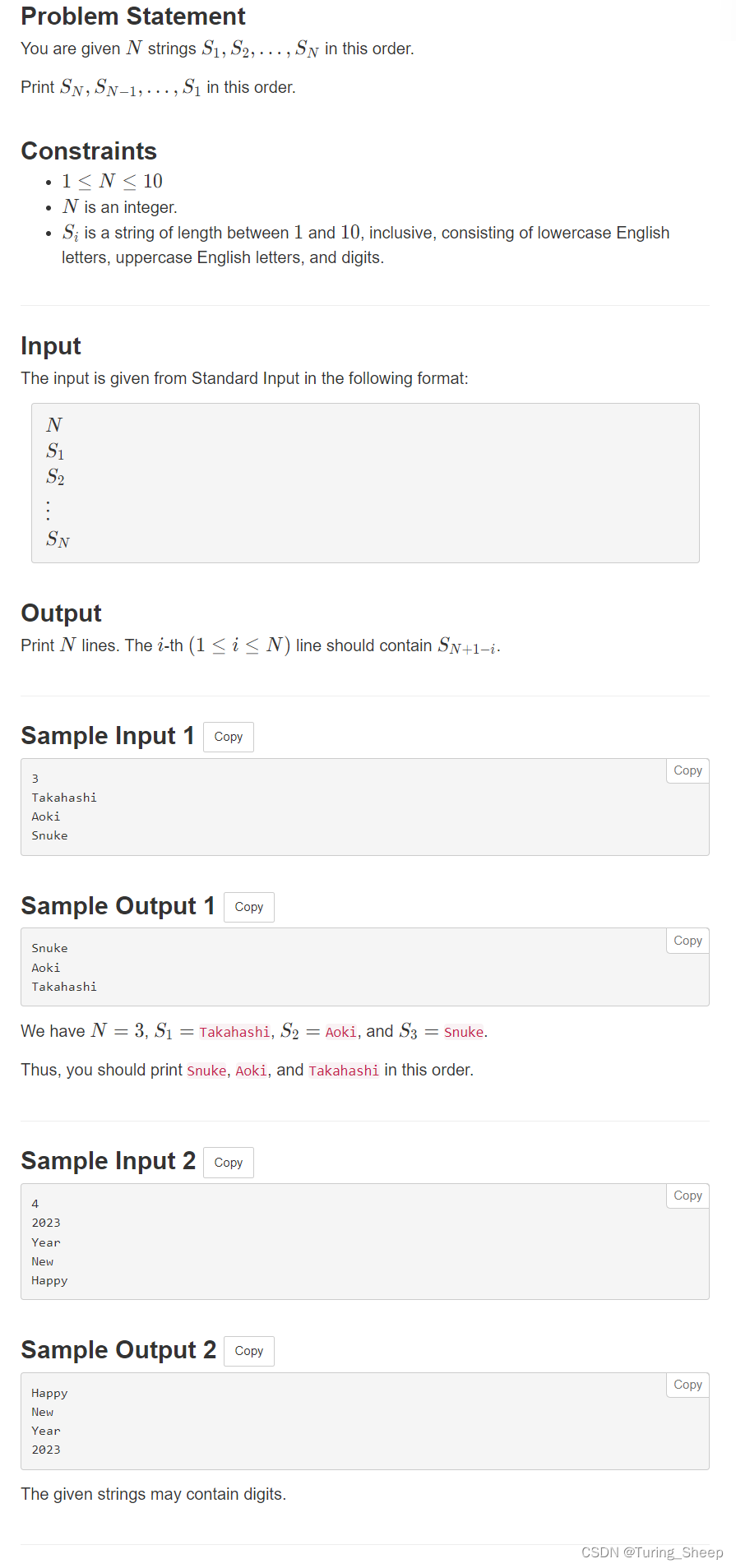
2、代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
string a[20];
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
for(int i=n-1;i>=0;i--)
{
cout<<a[i]<<endl;
}
return 0;
}
B - Multi Test Cases
1、问题
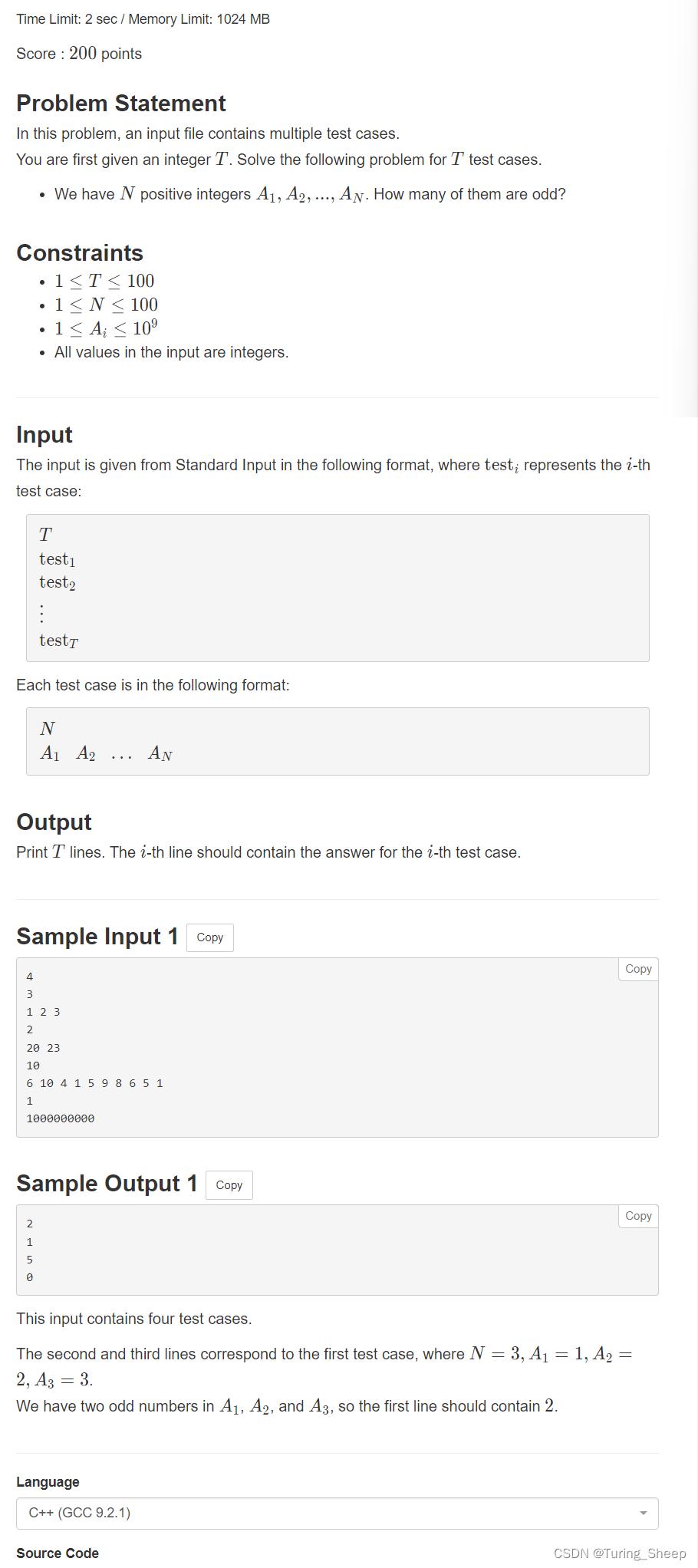
2、代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int count=0;
while(n--)
{
int a;
scanf("%d",&a);
if(a%2)count++;
}
cout<<count<<endl;
}
return 0;
}
C - Count Connected Components
1、问题:
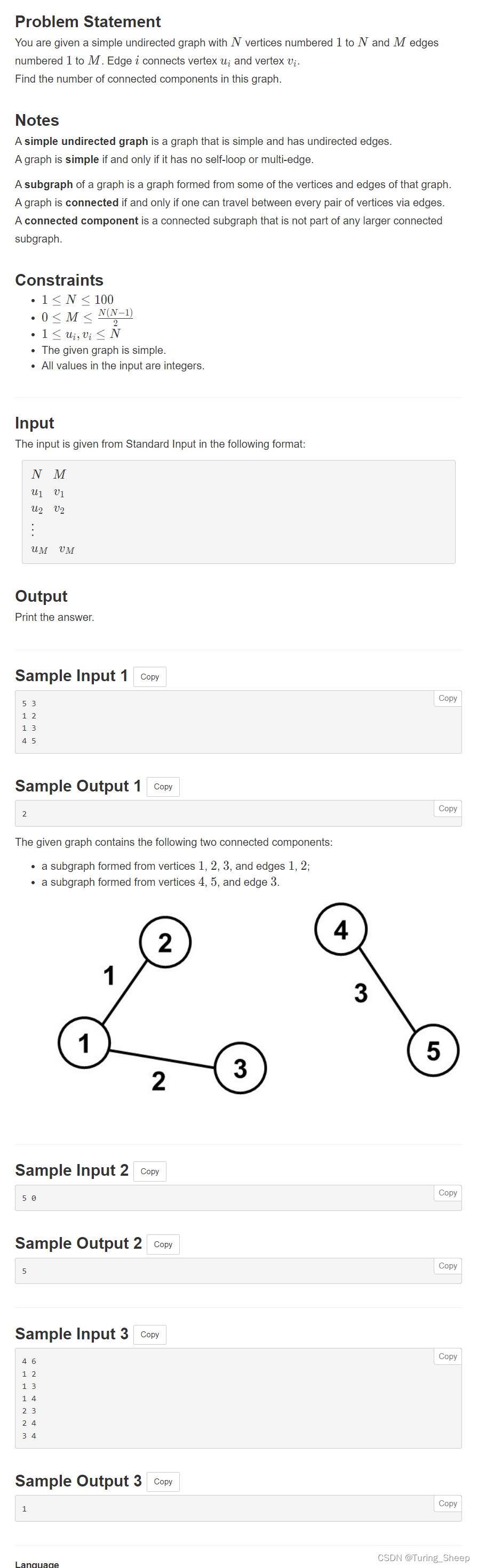
2、思路:——并查集、DFS
这道题说白了就是让你判断一个图分成了几个集合。
那么最直接的方法就是并查集。
第二种方法就是,DFS直接搜索,看我们搜索几次能够将整个图都遍历一次。
3、代码
方法1:并查集
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=200;
int p[N];
int cnt[N];
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)p[i]=i,cnt[i]=1;
while(m--)
{
int x,y;
cin>>x>>y;
int px=find(x),py=find(y);
if(px!=py)
{
cnt[py]+=cnt[px];
cnt[px]=0;
p[px]=py;
}
}
int nums=0;
for(int i=1;i<=n;i++)
{
if(cnt[i])nums++;
}
cout<<nums<<endl;
return 0;
}
方法2:DFS
//DFS
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=210,M=1e5;
int h[N],e[M],ne[M],idx;
bool st[N];
int ans;
void add(int x,int y)
{
e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
void dfs(int u)
{
if(st[u])return;
st[u]=true;
for(int i=h[u];i!=-1;i=ne[i])
{
if(!st[e[i]])
{
dfs(e[i]);
}
}
}
int main()
{
memset(h,-1,sizeof h);
int n,m;
cin>>n>>m;
while(m--)
{
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
ans++;
dfs(i);
}
}
cout<<ans<<endl;
return 0;
}
D - Happy New Year 2023
1、问题
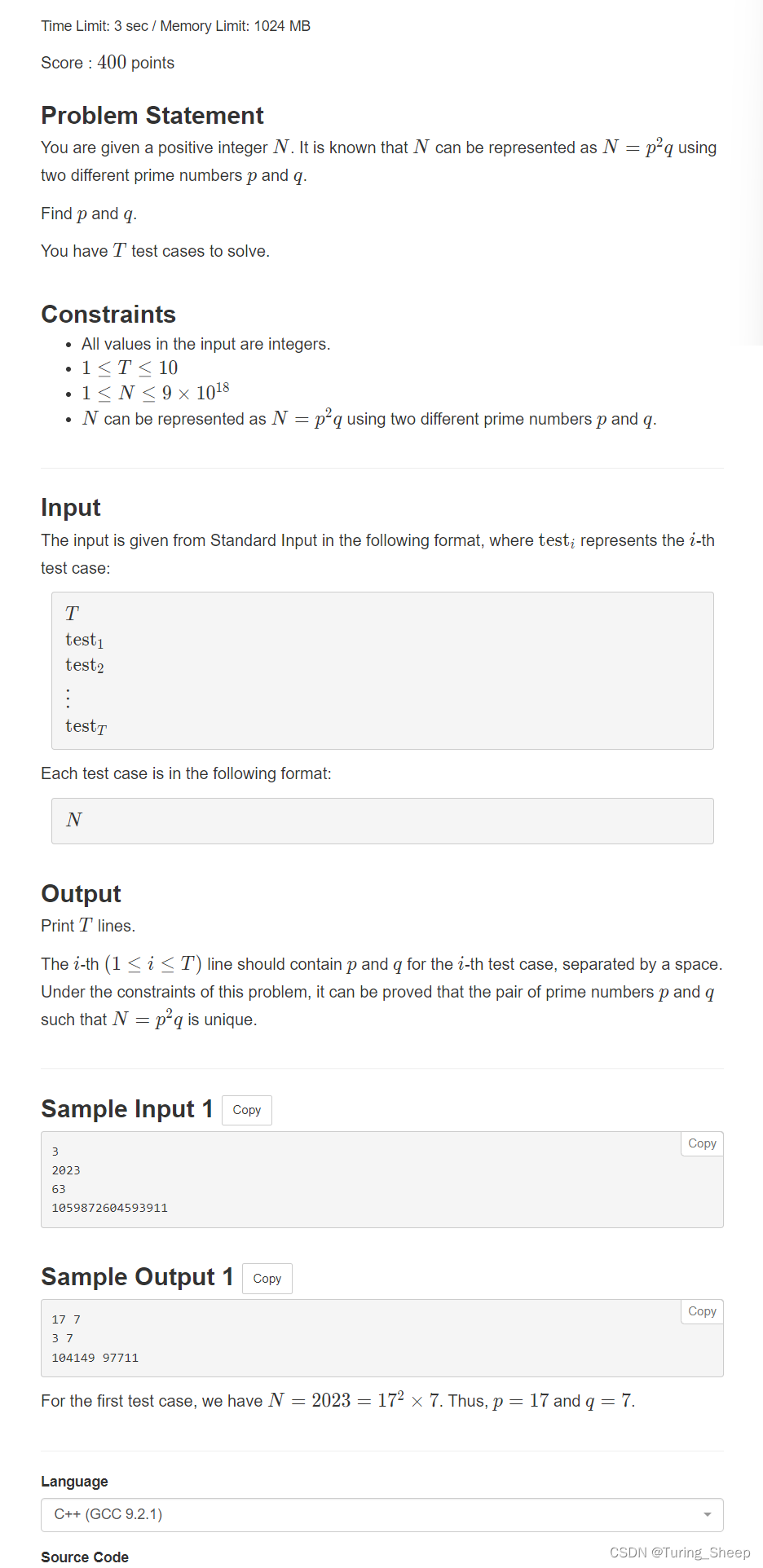
2、思路——算数基本定理、欧拉筛
方法一:欧拉筛
这道题的数据范围非常的大,就算我们用O(N)的算法去遍历也会超时,并且超时非常严重。数据范围是: 9 × 1 0 18 9×10 ^{18} 9×1018,而1秒之内,c++最多运算 1 0 9 10^9 109次。
所以只能想别的办法:
将一个数拆成三个数相乘的模式,那么这三个数当中的最小值 x m i n x_{min} xmin。必定满足 x m i n ≤ n 3 x_{min}\leq \sqrt[3]{n} xmin≤3n。
证明的话,显而易见,如果不满足的话,三个数相乘的结果就会大于n。
所以,我们可以去枚举最小值,因为这个最小值要么是 p p p,要么是 q q q。知道其中一个就可以算另外一个。
我们枚举最小值的话,需要在质数中枚举,因此我们可以利用欧拉筛,筛选出质数。我们筛的范围只需要是范围的最大值开三次方,大概是 3 ∗ 1 0 6 3*10^6 3∗106。
但是,现在就有一个问题了。
我们怎么知道我们利用最小的数算出来的那个就是质数呢?
由于这个数可能是大于开三次方的那个范围,因此,我们是不能够查表的。而单独判断的话,时间复杂度是 O ( n ) O(\sqrt n) O(n)。这个复杂度的话,还是会超时。因此,两种方法都行不通。
我们只能从数学的角度分析一下了。
我们的疑问点在于,万一算出来的不是质数是合数怎么办?
根据算数基本定理,一个数可以写成有限个质因数相乘的形式,并且形式是唯一的。
而这道题最后是拆成了三个质数,因此这就是算术基本定理表达结果。根据定理中的唯一性,当我们已经知道其中一个质数的时候,必定能通过计算算出另外一部分相乘的部分。
根据题意, N = p 2 ∗ q N=p^2*q N=p2∗q
也就是说,我们已经知道了这个数字的算数基本定理的表达形式。
假设我们知道了 q q q,那么算出来的一定是一个质数的平方。
假设我们知道了 p p p,那么我们平方之后再算出来的那个一定是另外一个质数 q q q。
所以我们只需要知道其中一个质数即可。
但是,上述的方法依旧是多此一举的方法。
方法二:算数基本定理
我们根本没有必要去利用欧拉筛提前选出所有的质数。
因为,只要是我们从2开始枚举,第一次枚举到的就是质数。
证明:
因为是第一次枚举到的,说明从 2 2 2到 i − 1 i-1 i−1都没能够整除我们的 n n n。假设我们第一次枚举到的是一个合数,那么这个合数能够分解成更小的质数,这个更小的质数会在次之前被枚举到,如果存在这个数,必定能够整除我们当前枚举到的i,也必定能够整除n。但是在次之前都没有一个数能够整除n。说明我们的假设矛盾,所以不存在这样的可能。
所以我们第一次美枚举到的一定是质数。
当我们知道了质数之后,根据算术基本定理的唯一性,我们就能够从枚举出来的质数出发直接算出另一部分。
3、代码
欧拉筛版本
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=3e6+10;
typedef long long ll;
int primes[N],cnt;
bool st[N];
void euler()
{
int n=3e6;
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;i<=n/primes[j];j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int main()
{
euler();
int t;
ll n;
cin>>t;
while(t--)
{
cin>>n;
for(int i=0;i<cnt;i++)
{
if(n%primes[i]==0)
{
if((ll)(n/primes[i])%primes[i]==0)
{
int p=primes[i];
ll q=n/p/p;
cout<<p<<" "<<q<<endl;
break;
}
else
{
int q=primes[i];
ll p=(ll)sqrt(n/primes[i]);
cout<<p<<" "<<q<<endl;
break;
}
}
}
}
return 0;
}
算数基本定理
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=3e6+10;
typedef long long ll;
int main()
{
int t;
ll n;
cin>>t;
while(t--)
{
cin>>n;
for(int i=2;i*i*i<=n;i++)
{
if(n%i==0)
{
if((ll)(n/i)%i==0)
{
int p=i;
ll q=n/p/p;
cout<<p<<" "<<q<<endl;
break;
}
else
{
int q=i;
ll p=(ll)sqrt(n/i);
cout<<p<<" "<<q<<endl;
break;
}
}
}
}
return 0;
}
E - Sequence of Strings
1、问题
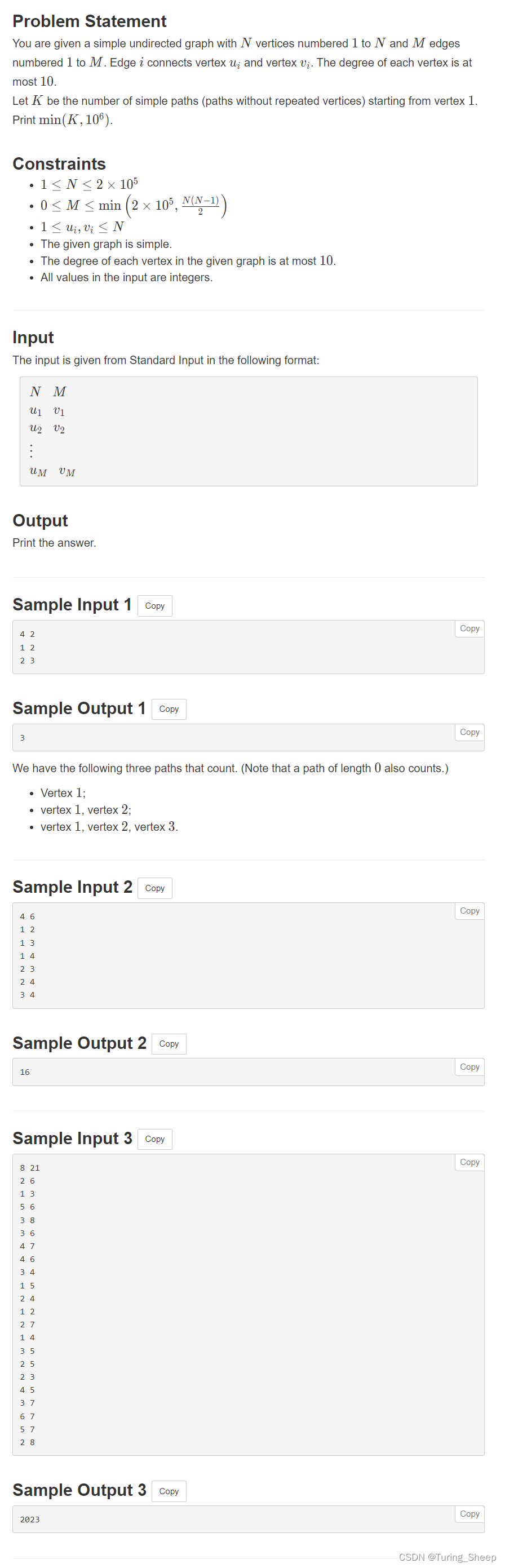
2、思路——DFS
直接DFS就行了,走到一个节点就+1,遇到重复的就返回。
3、代码
链式前向星版邻接表
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2e5+10,M=2*N;
int h[N],e[M],ne[M],idx;
bool st[N];
int ans=1;
void add(int x,int y)
{
e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
void dfs(int u)
{
if(ans>=1e6)
{
cout<<1000000<<endl;
exit(0);
}
st[u]=true;
for(int i=h[u];i!=-1;i=ne[i])
{
if(!st[e[i]])
{
ans++;
dfs(e[i]);
st[e[i]]=false;
}
}
}
int main()
{
memset(h,-1,sizeof h);
int n,m;
cin>>n>>m;
while(m--)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
dfs(1);
cout<<ans<<endl;
return 0;
}
vector版邻接表
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N=2e6+10;
vector<int>a[N];
bool st[N];
int ans=1;
void dfs(int u)
{
if(ans>=1e6)
{
cout<<1000000<<endl;
exit(0);
}
st[u]=true;
for(auto x:a[u])
{
if(!st[x])
{
ans++;
dfs(x);
st[x]=false;
}
}
}
int main()
{
int n,m;
cin>>n>>m;
while(m--)
{
int x,y;
scanf("%d%d",&x,&y);
a[x].push_back(y);
a[y].push_back(x);
}
dfs(1);
cout<<ans<<endl;
return 0;
}