今天读的是发表在WACV2023上的MVS文章，该文章提出了基于全景相机的MVS pipeline。
文章链接：点击前往
代码链接：暂未开源。

Abstract

随着深度学习技术的进步，最近的多视图立体方法取得了可喜的成果。 尽管取得了进展，但由于常规图像的视野有限，重建大型室内环境仍然需要收集许多具有足够视觉重叠的图像，这是相当劳动密集型的。 360° 图像覆盖的视野比常规图像大得多，并且有助于捕获过程。 在本文中，我们介绍了 360MVSNet，这是第一个用于具有 360° 图像的多视图立体的深度学习网络。 我们的方法将不确定性估计与球形扫描模块相结合，用于从多个视点捕获的 360° 图像，以构建多尺度成本量。 通过以粗到细的方式回归体积，可以获得高分辨率的深度图。 此外，我们还构建了 EQMVS，这是一个大型合成数据集，由等距柱状投影中超过 50K 对 RGB 和深度图组成。 实验结果表明，我们的方法可以重建大型合成和真实世界的室内场景，其完整性明显优于以前的传统和基于学习的方法，同时在数据采集过程中节省了时间和精力。

1. Introduction

介绍了MVS的一般流程和当前状况下的问题，全景相机发展很好，尽管可以将 360° 图像变形为多个透视图图像，然后应用经典的 MVS 方法，但它不是最优的，因为它忽略了 360° 图像中的连续几何信息。
本文贡献有两个：

1. 提出了首个基于全景相机的MVS框架。
2. 提出了EQMVS，一个大规模的 360° 图像合成 MVS 数据集。

2. Related works

介绍了传统MVS、基于深度学习的MVS和全景相机的深度估计与立体匹配。

3. Method

我们的目标是从一组 360° 图像重建 3D 场景结构。 与以前的方法类似，我们的方法遍历图像并一次预测它们的深度图。 每次，我们的方法都会选取一个参考图像并使用 N 个附近的源图像估计其深度图。 在估计所有深度图之后，将它们合并在一起以产生最终的场景点云。 图 2 描述了我们的网络架构，用于预测具有一组源图像的参考图像的深度图。 为了生成高分辨率的深度图，我们的模型以从粗到精的方式工作。 它由三个不同尺度的阶段组成，从最粗糙的阶段开始。 在每个阶段，我们的方法首先为所有输入的 360° 图像提取特征（第 3.1 节）。 然后，它使用建议的 360° 球面扫描算法（第 3.2 节）将源特征映射到以参考视图为中心的多个虚拟球体上，并构建成本量（第 3.3 节）。 最后，将成本量回归到预测的深度图中（第 3.4 节）。

3.1 Feature Extraction

我们的第一步是提取 $N+1$ 个输入图像的特征图 { F i } i = 0 N \{F_{i}\}^{N}_{i=0} {Fi​}i=0N​，其中 $I_0$ 是参考图像，其余的是源图像。 为了捕获不同分辨率的信息，我们采用具有跳跃连接的 U-Net 结构来形成多尺度特征提取器。 具体来说，编码器包含一组卷积层，每个卷积层后跟一个批量归一化和一个 ReLU 激活层。 步幅为 2 的卷积用于逐步下采样特征图的空间维度。 解码器层对特征进行上采样并与来自skip connection的特征连接。 然后应用转置卷积逐渐恢复图像信息。 对于第 $i$ 个源图像 $I_i$，特征提取器在三个不同的尺度上提取其特征图 $F_i=(F_i^1,F_i^2,F_i^3)$。 三个特征图的分辨率分别为 $\frac{W}{4}\times \frac{H}{4}$ 、$\frac{W}{2}\times \frac{W}{2}$ 和 $W\times H$，其中 $(W,H)$是输入 360° 图像的宽度和高度。

3.2 360 Spherical Sweeping

我们提出了一种 360 度球形扫描模块，该模块考虑了来自 360° 图像的几何信息。 我们的模块受到平面扫描和鱼眼球面扫描算法的启发。 它将等距柱状图像的特征图变形到具有不同半径的参考视图的虚拟球体上，以形成cost volume。 该模块是完全可微分的。 因此，我们可以将其无缝集成到我们的训练过程中。 我们的方法与以前的球形扫描算法之间的主要区别是两个。 首先，我们的网络使用 360° 图像作为输入。 其次，以前的方法旨在从单个视点估计全向深度图，而我们遵循大多数 MVS 方法的惯例，并使用从多个不同视点捕获的图像重建场景几何。 因此，在估计参考视图的深度图时，我们的 360° 球面扫描算法需要推导出两个视点之间的关系，然后基于两个 360° 图像构建cost volume。

3.2.1 Preliminary: Spherical coordinates

球坐标和相机坐标之间的映射。 图 3 (a) 定义了本文中使用的球形相机模型。 在360°相机的3D相机坐标系中，点$P(X,Y,Z)$可以用归一化球坐标$(R,\Theta ,\Phi )$表示，其中$R,\Theta ,\Phi$分别为到原点的距离、仰角和方位角。 我们可以通过计算将点从 3D 相机坐标系转换到归一化球坐标系：

具体来说，$\Theta \in (-\frac{\pi }{2},+\frac{\pi }{2})$ 和 $\Phi \in (-\pi ,+\pi )$。 我们还可以通过以下方式将归一化球坐标映射到 3D 相机坐标：

图像和球面坐标之间的映射。 我们使用具有经纬度投影的等距柱状图像来存储 360° 相机捕获的场景信息。 从分辨率为 $W\times H$ 的等距柱状图像中的像素 $(x,y)$ 到球坐标中对应的单位向量的映射可以写为：

3D 和图像坐标之间的映射。 相机坐标中的 3D 点 $P(X,Y,Z)$ 到等距柱状图像坐标中的 2D 像素 $p(x,y)$ 的投影 $f(P)$ 可以通过引入仰角和方位角来获得：

其中，仰角和方位角可以通过公式 2 和公式 3 计算。

给定 2D 像素 $p(x,y)$ 的深度值 $d$，我们还可以使用 $f(P)$ 的反函数将 $p$ 从图像坐标反投影到其对应的 3D 坐标 $P(X,Y,Z)$：

其中 $\Phi$ 和 $\Theta$ 可以通过方程式5、6使用图像分辨率来计算。 注意，我们在球坐标中估计的深度值是点与球体原点之间的距离（即 $R$），而不是传统针孔相机中的深度值。

3.2.3 Feature map warping

为了构建cost volume，我们的 360 度球形扫描将源图像的特征图warp到一系列虚拟球体上，这些虚拟球体基于深度假设具有不同的半径（图 3 (b)）。 我们使用外参来连接参考视图和源视图的局部相机坐标。 将一个点从参考视图投影到第 $i$ 个源视图的投影 $M_i$ 可以通过concatenate矩阵 $P_0^{-1}$ （将一个点从参考视图的相机坐标转换为世界坐标）和矩阵 $P_i$（从世界坐标转换为第 $i$ 个源视图的相机坐标） 来获得：

其中$P_i$是第$i$个视角的满秩的$4\times 4$矩阵：

$R_i$和$T_i$分别是旋转矩阵和平移向量。

现在，我们可以使用以下反向warp过程将第 $i$ 个源特征变形到以参考视图为中心的半径为 $r_k$ 的第 $k$ 个虚拟球体上：对于变形特征图中的每个像素 $p(x,y)$，我们首先将其转换为球坐标，并投影到具有深度假设 $r_k$ 的参考视图的 3D 相机空间。 然后使用等式 9 将 3D 点转换为第 $i$ 个源摄像机的摄像机坐标。最后，我们将 3D 点投影到第 $i$ 个源视图的特征图上并得到源位置 $p_k^i(x_k^i,y_k^i)$，然后 使用双线性插值对特征图重新采样。 warp特征图的源位置计算可以写成：

值得注意的是，我们的工作和 OmniMVS 处理不同的场景。 OmniMVS 的目标是从“单一视点”估计全向深度图。 他们使用从四个鱼眼相机的装备收集的信息来预测 360° 深度图。 相比之下，按照大多数 MVS 方法的惯例，我们旨在通过使用从“多个不同视点”捕获的多个 360° 图像来重建整个场景的几何形状。 因此，在估计参考视图的深度图时，我们的 360° 球面扫描算法需要导出两个视点之间的关系，然后基于这两个 360° 图像构建cost volume。 对于 OnmiMVS 和 SweepNet 提出的方法，情况并非如此。

3.3 Multi-scale Cost Volume

在使用 360 球面扫描将源视图的特征图变形到参考视图的虚拟球体后，我们聚合变形的特征图以构建具有基于方差的成本度量的cost volume。 受最近的多尺度 MVS 工作的启发，成本量以从粗到细的方式构建，用于存储深度假设的自适应信息。 如图 2 所示，这三个阶段使用预定义数量的深度假设构建成本量：$D_1$、$D_2$ 和 $D_3$。 在第一阶段（最粗糙的阶段），我们在预定义的深度区间 $[dmin,dmax]$ 内均匀采样 $D_1$ 深度假设，因为此时我们没有任何关于场景深度的信息。

在第二和第三阶段，对于warped feature map中的每个像素，我们根据从前一阶段正则化的深度概率体积（在第 3.4 节中讨论）的不确定性设置其球体半径范围以进行深度假设。 假设深度值服从高斯分布，我们可以通过计算阶段$s$中像素$x$处的标准差$\sigma$来估计深度概率体积的逐像素不确定度：

其中$P_s^j$ 、$d_s^j(x)$ 和${\hat{d}}_s(x)$ 分别表示第 $j$ 个深度假设球体的概率体、第 $j$ 个假设球体的预测深度和第 $j$ 个深度假设。 $D_s$ 表示假设球体的数量。

利用前一阶段估计的深度值分布，基于confidence interval的思想，我们逐步缩小下一个阶段的假设范围。 我们在阶段 $s$ 中为深度图中的像素 $x$ 设置假设范围 $R_s(x)$：

对于本文中的所有结果，$\lambda$ 的值都设置为 $1.5$。 我们观察到结果对 $\lambda$ 的值不敏感，因为模型会通过训练学习调整不确定性区间。 通过空间变化的不确定性估计，我们可以有效地缩小深度间隔并减少深度样本的数量。

3.4 Depth Regression and Loss Function

我们应用 3D CNN 来规范cost volume并生成probability volume。 具体来说，正则化网络是一个 3D U-Net，由一系列考虑不同分辨率特征的下采样和上采样层组成。 在卷积层之后，沿深度方向对概率体积应用 softmax 操作。 最后，我们的网络输出估计的深度值作为根据所有深度假设计算的预期值：$D={\Sigma }_{d=d_{min}}^{d_{max}}d\times P(d)$，其中 $d_{min}$ 和 $d_{max}$ 分别表示最小和最大深度样本。

继之前的工作之后，我们将深度估计视为一个多类回归问题，我们的损失函数使用 $L1$ 范数来衡量地面真实深度与估计深度之间的差异。 因为三个阶段的代价量是分别正则化的，所以总损失是三个阶段的$L1$损失的加权和：

其中 D = { D s } s = 1 N D = \{D^{s}\}^{N}_{s=1} D={Ds}s=1N​, D G T = { D G T s } s = 1 N D_{GT} = \{D^{s}_{GT}\}^{N}_{s =1} DGT​={DGTs​}s=1N​, $P_{valid}$ 是真实深度中有效像素的集合，${\lambda }_s$ 是第 $s$ 阶段的权重。

4. Synthetic Dataset: EQMVS

要通过监督学习训练我们的 360MVSNet，具有等距柱状投影的多视图立体数据集是必不可少的。 然而，现有的多视图立体数据集（如 DTU）仅包含具有透视图像的以对象为中心的场景。 为了解决这个问题，我们提出了等距柱状格式的室内场景图像的大规模合成数据集 EQMVS。

4.1 Data Acquisition

描述了数据集是如何制作的。

5. Experiments and Results

5.1 Implementation Details

训练。使用单块Quadro RTX8000的GPU。 按照 MVSNet，输入图像的数量设置为 $N=3$，其中 1 个参考图像和 2 个源图像。 我们采用三尺度cost volume，每个阶段的深度假设数分别为 160、32 和 8。我们将 EQMVS 中的场景分成包含 825 个场景的训练集和包含其余 189 个场景的测试集。

后处理。与之前基于深度图的 MVS 方法类似，我们的方法需要一个后处理步骤来将预测的深度图转换为点云。 因为 360° 图像没有现有的深度融合方法，所以我们在合并深度图时应用简单的过滤规则来去除异常值。 我们考虑预测深度图之间的光度和几何一致性：为了光度一致性，我们过滤掉概率低于 0.3 的像素。 为了几何一致性，我们相互投影视图之间的像素以确保深度值一致。

5.2 Performance

Equal-effort quantitative evaluation。 我们遵循 DTU 数据集提出的标准评估指标来计算重建点云的准确性和完整性。 精度度量测量从估计点云到地面实况点云的距离。 完整性度量测量从地面实况点云到估计点云的距离。 我们还评估了 MVSNet 引入的总体得分，该得分取准确性和完整性的平均值。 我们在 EQMVS 测试集上将我们的方法与传统的基于几何的方法和基于学习的方法 MVSNet 进行了比较。 我们不与后来建立在 MVSNet 上的方法进行比较，因为它们专注于减少内存消耗。 我们不将我们的方法与 OmniMVS 和 SweepNet 进行比较，因为目标不同。 在这个实验中，我们对所有方法都使用在相同位置捕获的输入图像，这意味着收集输入数据需要类似的努力。 因为我们的方法是第一个使用 360° 图像作为输入的基于学习的方法，为了进行公平比较，输入测试图像从等矩形投影扭曲到立方体贴图投影用于以前的方法以避免失真，因为以前的工作都是正常的 FoV 图像。 我们选择立方体贴图投影是因为它是计算机图形学中最常用的表示法，用于用透视图像表示球面数据。 如表 1 所示，我们的方法在完整性和总体得分方面优于所有其他方法。 我们在图 4 中展示了定性结果。由于篇幅限制，我们只能从一个角度展示重建结果。与其他方法相比，我们的方法由于其广泛的 FoV 和单个 360° 图像中的连续信息而对视觉重叠区域的区域不太敏感。 相比之下，其他方法很难重建整个环境，而且通常只能恢复场景的一小部分区域。

对摄像头数量的评估。 图 5 中的实验表明，以前的方法需要大约 500 张图像才能实现与我们的方法相似的完整性和整体质量得分，后者仅使用 25 张图像。 这表明用户必须花费大约 20 倍的努力来收集以前方法的数据。 我们的方法在准确性得分方面不那么令人印象深刻。 原因是由于缺乏 360° 图像的深度融合算法，我们在合并深度图时仅应用简单的过滤规则。 因此，我们不能像其他方法那样以稳健的方式剔除异常值。 我们把它留作未来的工作。 然而，值得注意的是，以前的方法无法重建只有 25 张图像的场景。

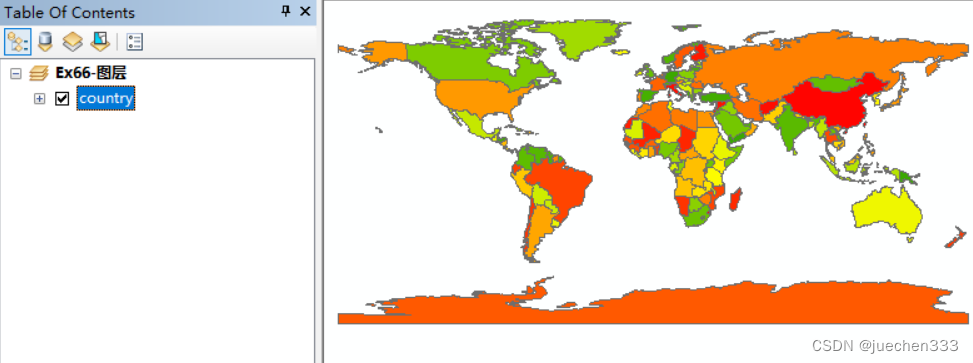
真实世界 360° 图像的定性结果。 为了证明我们提出的模型的泛化能力，我们用等矩形格式的真实世界图像测试我们的模型。 图像的相机位置由 OpenMVG 恢复。 图 6 显示了与场景中其他方法的比较。 我们的方法可以仅使用 11 张 360° 图像重建大部分场景，而其他方法使用 66 张图像但只能重建场景的一小部分。 虽然我们的模型是在合成图像上训练的，没有对真实世界的数据进行任何微调，但它在真实世界的场景中显示出很高的鲁棒性。

6. Conclusions and Future Works

在本文中，我们提出了 360MVSNet，这是一种基于深度学习的多视图立体方法，可以从 360° 图像重建室内场景的 3D 结构。 我们提出了一种新颖的 360 度球形扫描模块，并用它来构建多尺度cost volume。 可以通过对cost volume进行回归来获得高分辨率深度图。 然后我们将所有视图的深度图合并在一起以重建最终的场景点云。 我们还展示了一个用于训练 360MVSNet 的大规模合成数据集 EQMVS。 我们证明了我们的方法在所有比较方法中实现了最好的重建结果。

有许多限制值得进一步研究。 首先，我们的方法需要为输入的 360° 图像估计相机参数，而 360° 图像的运动结构 (SfM) 方法不如正常 FoV 图像的稳健性。 同样，目前还没有用于 360° 图像的深度图融合算法。 我们想探索 360° 图像的 SfM 和深度融合算法。 另一个问题是缺乏用于多视角立体的具有 360° 图像的真实室内环境数据库。 将来，我们很乐意使用多个 360° 图像捕捉更多真实世界的场景。