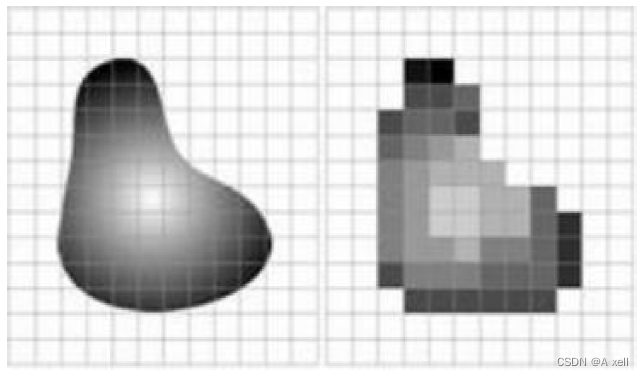
像素
- 像素是分辨率的单位;
- 构成位图图像的最基本单元;
- 每个像素都有自己的颜色;
图像分辨率
- 单位英寸内的像素点数;
- 单位为PPI(Pixels Per Inch),为像素每英寸;
- PPI表示每英寸对角线上所拥有的像素数目:
,x:长度像素数目,y:宽度像素数目,Z:屏幕大小;
- 屏幕尺寸(大小)指的是对角线长度;
- 图像清晰度的评价指标;
颜色模型
- 色彩三原色(CMYK):品红,黄,青;
- 光学三原色(RGB):红\绿\蓝;

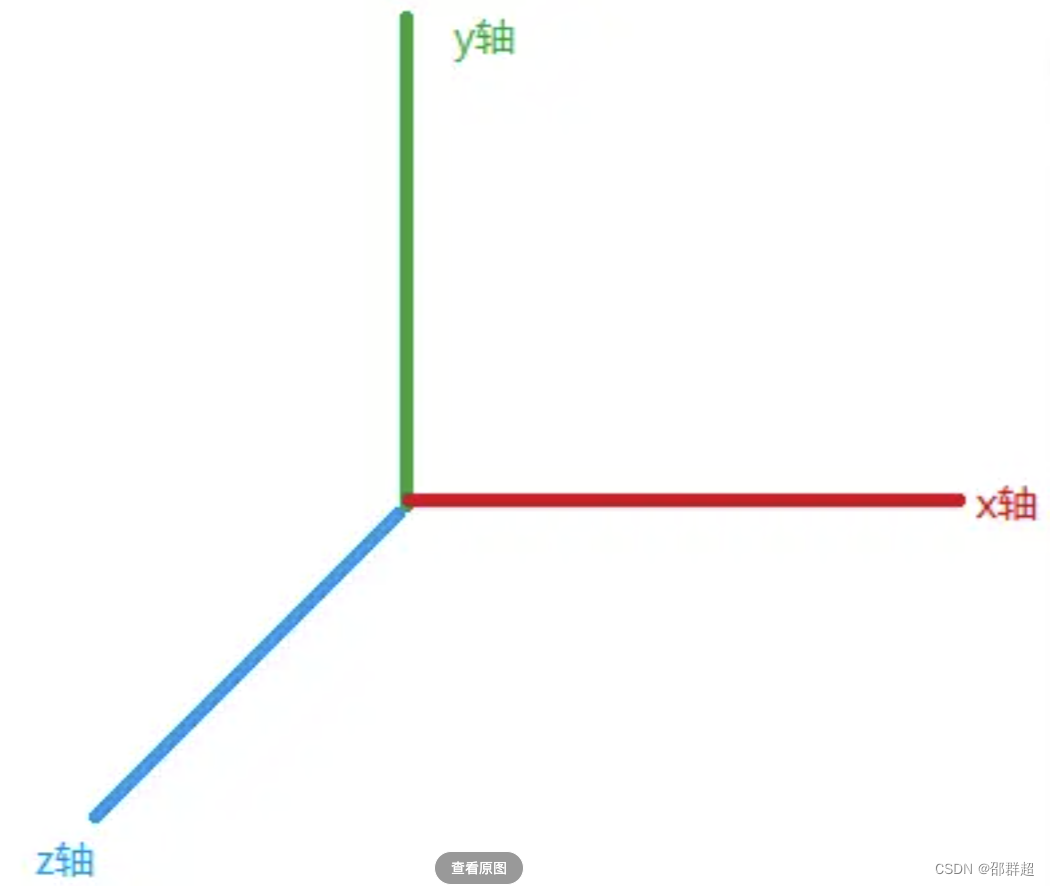
RGB模型
- 三维直角坐标颜色系统中的一个单位正方体;
- 正方体的主对角线上,各原色的量相等;
- 产生由暗到亮的白色,即灰度;
- 正方体的其他六个角点分别为红\黄\绿\青\蓝\品红;

灰度
- 表示图像像素明暗程度的数值;
- 黑白图像中点的颜色深度;
- 范围一般为0~255;
- 白色为255,黑色为0;
通道
- 把图像分解成一个或多个颜色成分;
单通道
- 一个像素点只需一个数值表示;
- 只能表示灰度;
- 0为黑色,255为白色;
- 可表示二值图/灰度图;
三通道
- RGB模式;
- 把图像分为红\绿\蓝三个通道;
- 可以表示彩色;
- 全0表示黑色;
四通道
- RGBA模式;
- 在RGB的基础上加上alpha通道,表示透明度;
- alpha=0表示全透明;
对比度
- 不同颜色之间的差别;
- 对比度=最大灰度值/最小灰度值;
RGB转为Gray
- 浮点算法:
;
- 整数算法:
;
- 移位算法:
;
- 平均值阀:
;
- 仅取绿色:
;
RGB值转化为浮点数
- 浮点运算结果更精确;
- 整数运算中会丢失小数部分;
- 导致颜色值严重失真;
- 计算过程越多,失真越严重;
- 将RGB值转化为[0,1]浮点数:x/255即可;
二值化
- 阈值随意设置;
if(img_gray[i,j]<=0.5):
img_gray[i,j]=0
else:
img_gray[i,j]=1通用概念(库的安装和使用)
- 使用pip或者conda安装;
- 百度搜索python 安装xxx;
- 得到库的名称;
- 使用的时候用import引入;
- 不需要死记硬背函数;
- 需要使用的时候搜索函数名;
- 可了解函数用法和参数含义;
常用视觉库
- opencv:安装使用pip install opencv-python,使用时:import cv2
- matplotlib:安装使用pip install matplotlib,使用时:import matplotlib.pyplot as plt
- skimage:安装使用pip install scikit-image,使用时:import skimage;
opencv BGR
- opencv读进来的图片通道排列:B--G--R;
- 不是主流的R--G--B;
#opencv读入的矩阵时BGR,想转为RGB,可以这样:
img=cv2.imread('1.jpg')
img=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)图像频率
- 灰度值变化剧烈程度的指标;
- 是灰度在平面空间上的梯度;
图像幅值
- 在一个周期内;
- 交流电瞬时出现的最大绝对值;
- 也是一个正弦波;波峰到波谷距离的一半;
数字图像
- 计算机保存的图像都是一个个像素点,称为数字图像;
图像数字化过程
- 由图像的取样与量化来完成;
图像的取样
- 取样就是决定用多少点来描述一幅图像;
- 取样结果质量的好坏用图像的分辨率来衡量;
- 数字化坐标值称为取样;
- 若横向的像素数(列数)为M,纵向的像素数(行数)为N;
- 图像的总像素数为MxN个像素;
图像的量化
- 指要用多大范围的数值表示图像采样之后的一个点;
- 数字化图像的幅度值称为量化;
上采样
- 放大图像,或称上采样:upsampling或图像插值:interpolating;
- 放大原图像;
- 可将图像显示在更高分辨率的显示设备上;
下采样
- 缩小图像,或称下采样:subsampled,或降采样:downsampled;
- 使图像符合显示区域的大小;
- 生成对应图像的缩率图;
上采样原理
- 内插值
下采样原理
常用的插值方法
- 最临近插值;
- 单线性插值;
- 双线性插值;
最临近插值
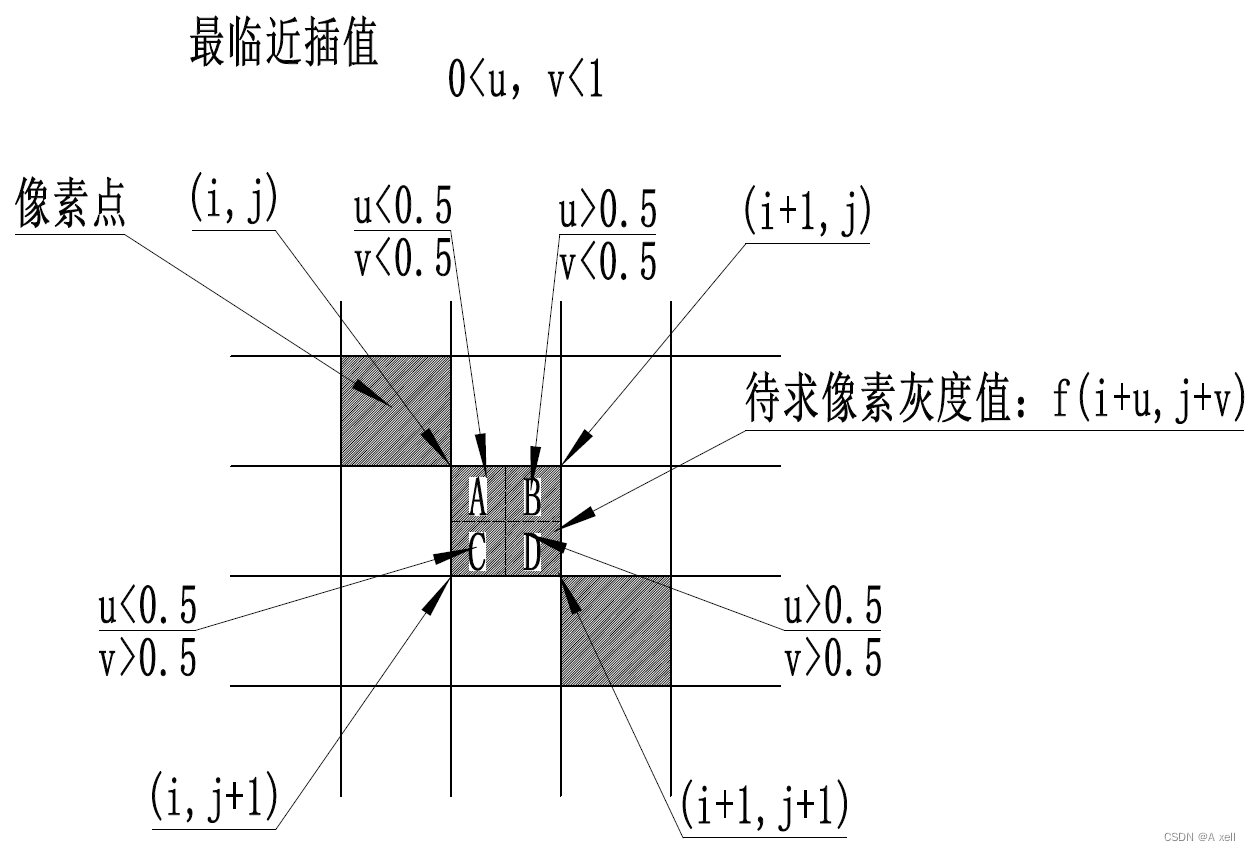
- The nearest interpolation;
- i+u,j+v为待求像素坐标;
- i,j为整数,u,v为大于零小于1的小数;
- 待求像素灰度值表示为f(i+u,j+v);
单线性插值
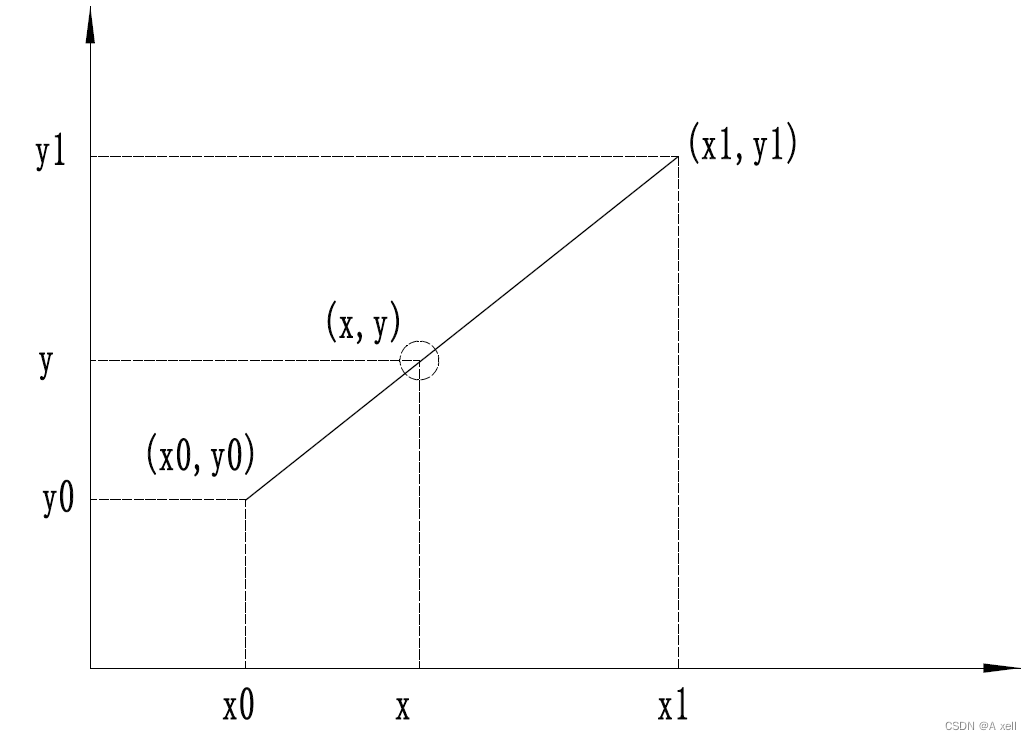
双线性插值
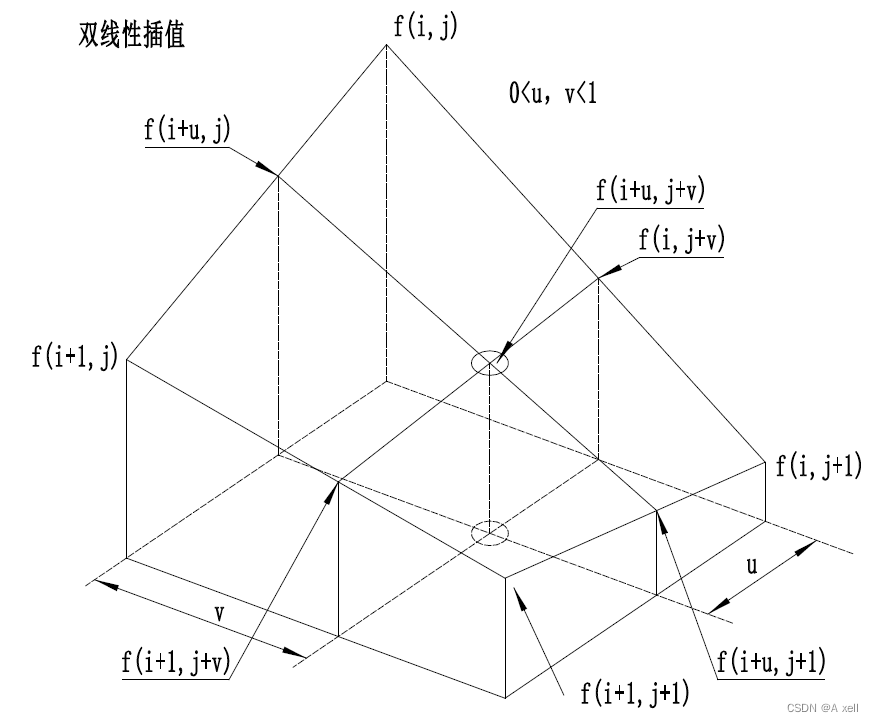
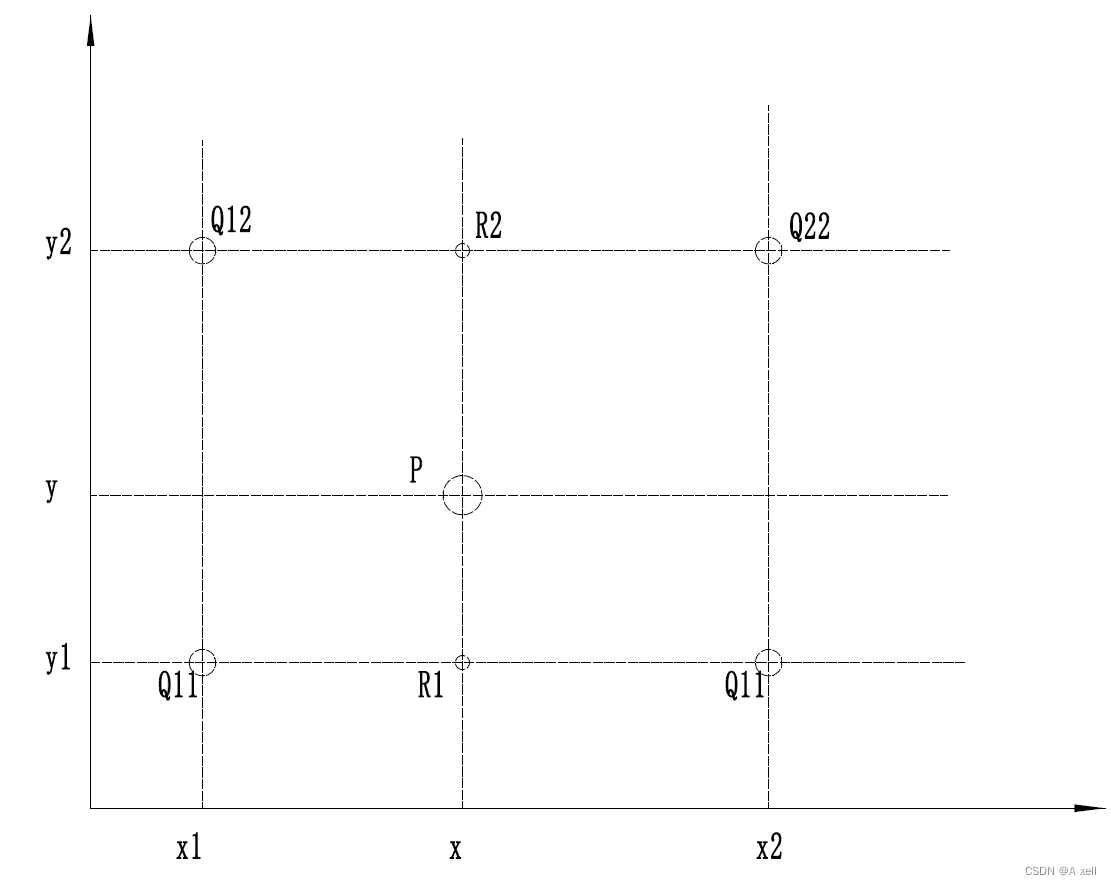
- 在x方向做插值:
- 在y方向作插值:
- 综合起来
- 图像双线性插值只用相邻的4个点,上述公式的分母都为1;
双线性插值坐标系的选择
- dst像素点的坐标对应到src图像当中的坐标;
- 通过双线性插值的方法算出src中相应坐标的像素值;
坐标对应关系
- 按比例对应:
源图像和目标图像的左上角对齐
- 如果源图像和目标图像的原点(0,0)均选择左上角;
- 根据插值公式计算目标图像每点像素;
- 假设需要将一幅5x5图像缩小为3x3;
- 源图像和目标图像各像素之间的对应关系如下图:

源图像和目标图像的中心对齐
- 两个图像的几何中心重合;
- 目标图像的每个像素之间等间隔;
- 目标图像的四边和源图像都有一定的边距;
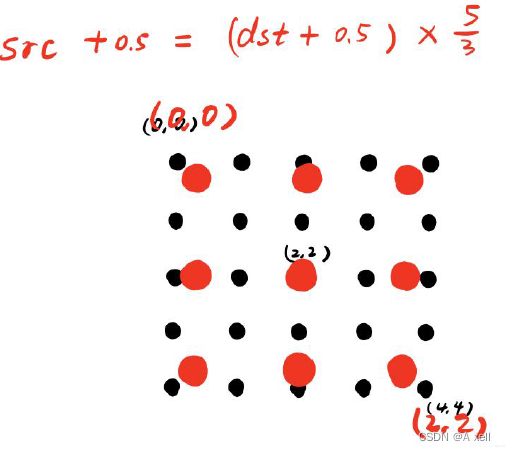
源图像和目标图像中心对齐平移参数的证明

双线性插值存在的问题
- 双线新插值较最临近插值算法复杂;
- 计算量较大;
- 但是没有灰度不连续的缺点;
- 图像看起来更光滑;
直方图
- 图像处理中,经常用到直方图:如颜色直方图,灰度直方图;
- 灰度直方图描述了图像中灰度分布的情况;
- 能够直观展示图像中各灰度级所占比例;
- 灰度直方图是灰度级的函数;
- 描述图像中该灰度级的像素的个数;
- 直方图中横坐标是灰度级;
- 纵坐标是该灰度级出现的频率;
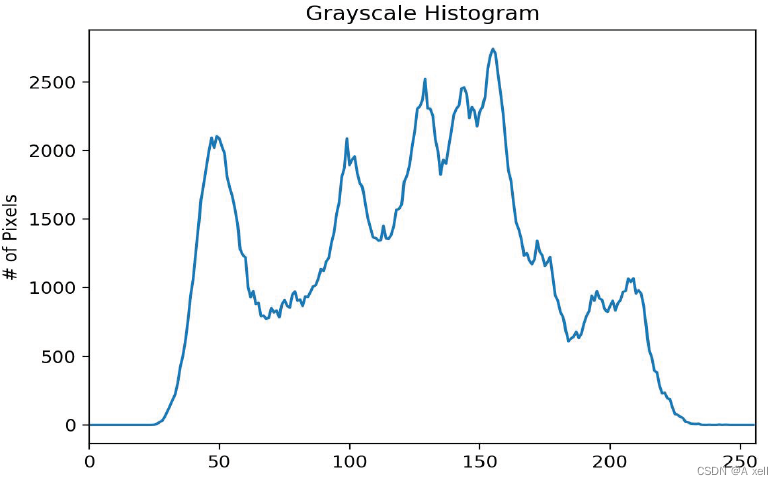
直方图的性质
- 反映图像中的灰度分布规律;
- 描述每个灰度级具有的像素个数;
- 不包含像素在图像中的位置信息;
- 不关心像素所处的空间位置;
- 不受图像旋转和平移变化的影响;
- 可以作为图像的特征;
- 任何图像都有唯一的直方图对应;
- 不同的图像可以有相同的直方图;
- 如果一幅图像有两个不相连的区域组成;
- 每个区域的直方图已知;
- 整幅图像的直方图是该两个区域的直方图之和;
直方图的应用
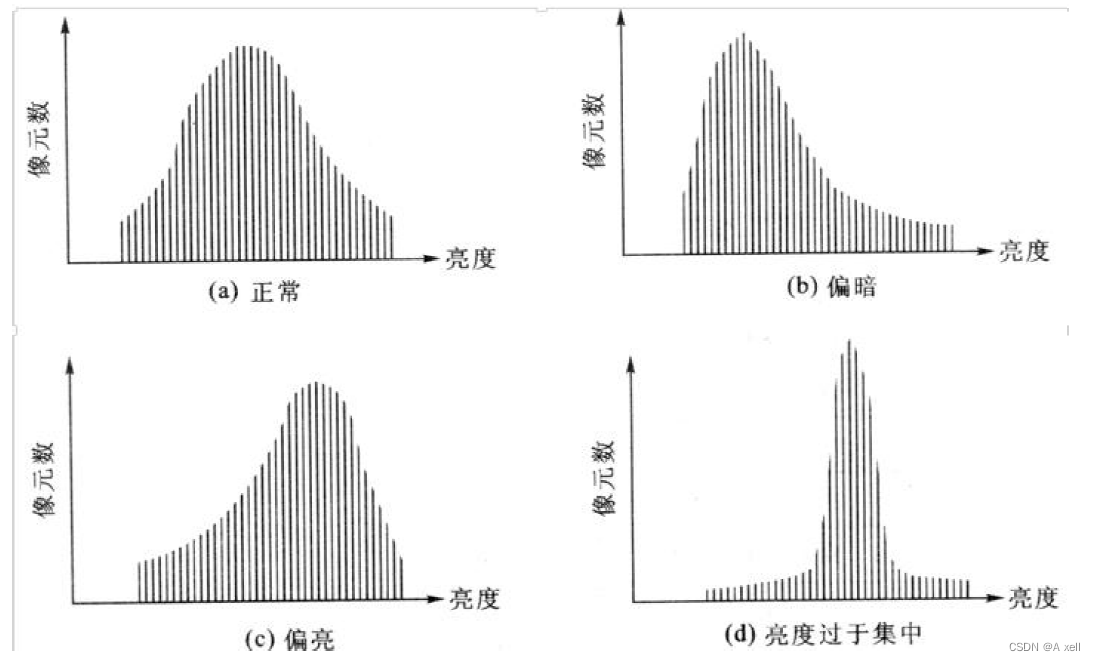
直方图均衡化
- 将源图像的直方图变换为均匀的直方图;
- 按均匀直方图修改原图像;
- 获得灰度分布均匀的新图像;
- 是用一定的算法使直方图大致平和的方法;
- 作用是图像增强;
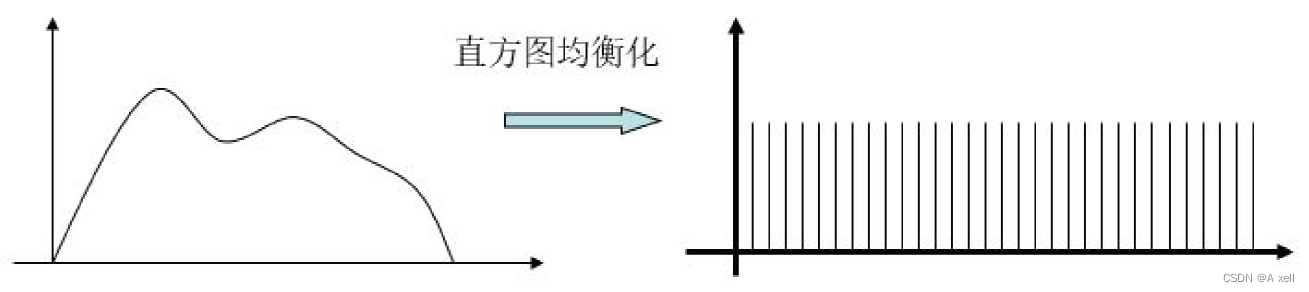
直方图均衡化的应用考虑
- 为了将原图像的亮度范围扩展;
- 需要一个映射函数;
- 将原图像的像素值均衡映射到新直方图中;
- 映射函数需要满足:
- 不打乱原有的亮暗布局;
- 映射后亮\暗的关系不改变;
- 且映射后必须在原有的范围内,比如(0-255);
直方图均衡化的步骤
- 依次扫描原始灰度图像的每一个像素;
- 计算出图像的灰度直方图H;
- 计算灰度直方图的累加直方图;
- 根据累加直方图和直方图均衡化的原理;
- 得出输入与输出之间的映射关系;
- 最后根据映射关系得出结果:
直方图均衡化的计算原理
- 输入图像的任意一个像素p,
;
- 总能在输出图像中有对应的像素q,
;
- 满足输入和输出的像素总量相等;
- 计算公式为(累加直方图公式):
- 输出图像每个灰度级的个数为:
- 代入累加直方图公式:
直方图均衡化实例
- 原图像矩阵,image:5x5,最大像素值max=9,最小像素值min=0;
| 1 | 3 | 9 | 9 | 8 |
| 2 | 1 | 3 | 7 | 3 |
| 3 | 6 | 0 | 6 | 4 |
| 6 | 8 | 2 | 0 | 5 |
| 2 | 9 | 2 | 6 | 0 |
- 直方图均衡化计算表格:
| 像素值 | 该像素 值数量 | 该像素值占图片 总像素值数量百分比: | 百分比 加合 | 四舍 五入 | |
| 0 | 3 | 3/25=0.12 | 0.12 | 29.72 | 30 |
| 1 | 2 | 2/25=0.08 | 0.2 | 50.2 | 50 |
| 2 | 4 | 0.16 | 0.36 | 91.16 | 91 |
| 3 | 4 | 0.16 | 0.52 | 132.12 | 132 |
| 4 | 1 | 0.04 | 0.56 | 142.36 | 142 |
| 5 | 1 | 0.04 | 0.6 | 152.6 | 153 |
| 6 | 4 | 0.16 | 0.76 | 193.56 | 194 |
| 7 | 1 | 0.04 | 0.8 | 203.8 | 204 |
| 8 | 2 | 0.08 | 0.88 | 224.28 | 224 |
| 9 | 3 | 0.12 | 1 | 255 | 255 |
- 目标图像矩阵
| 50 | 132 | 255 | 255 | 224 |
| 91 | 50 | 132 | 204 | 132 |
| 132 | 194 | 30 | 194 | 142 |
| 194 | 224 | 91 | 30 | 153 |
| 92 | 255 | 91 | 194 | 30 |
线性滤波
- 是图像处理的最基本方法;
- 允许对图像进行处理,产生很多不同效果;
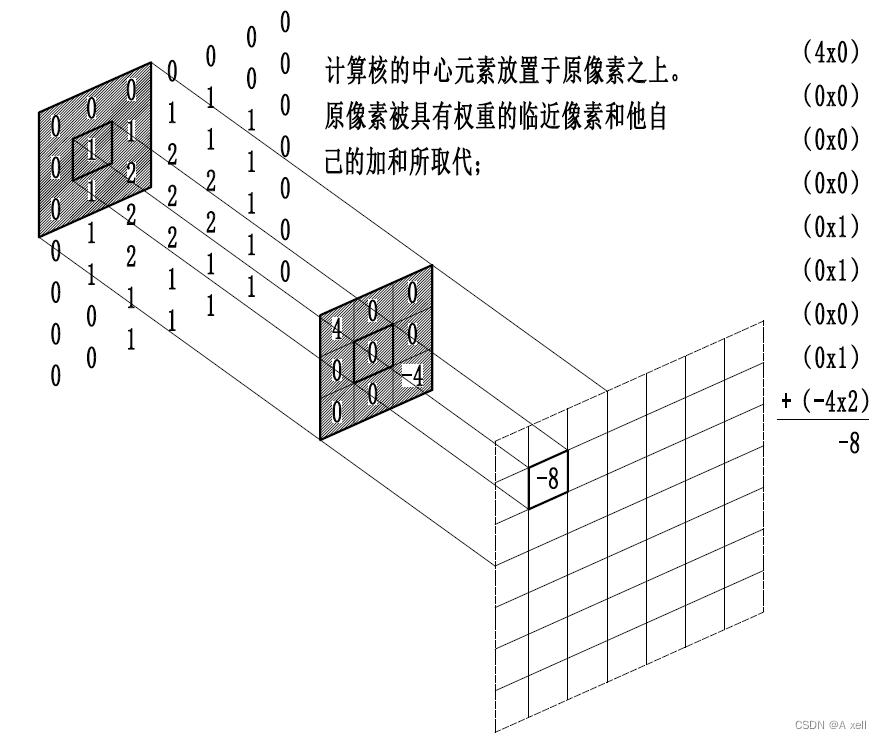
卷积
- 数学定义:
;
- g称为作用在f上的过滤器(filter)或者核(kernel);
过滤器/卷积核的要求
- 大小应为奇数;
- 奇数才有一个中心,比如3x3,5x5或者7x7;
- 有中心才有半径,比如,5x5的核半径为2;
- 滤波器矩阵所有元素之和应该等于1;
- 这样的核保证滤波前后图像的亮度保持不变;
- 但不是硬性要求;
- 如果滤波器所有矩阵的元素之和大于1;
- 滤波后的图像会比原图像更亮;
- 如果滤波器所有矩阵元素之和小于1;
- 滤波后的图像会比原图像更暗;
- 如果滤波器矩阵的所有元素和为0;
- 图像不会变黑,但会非常暗;
- 滤波后的图像像素值可能会出现负数或者大于255的情况;
- 大于255的直接截断;
- 负数取绝对值;
- 具体应用中的多卷积核;
- 认为每个卷积核代表一种图像模式;
- 图像与卷积核卷积出的值较大,说明图像值接近卷积核;
- 假设我们设计了6个卷积核;
- 可以理解,我们认为该图像上有6种底层纹理模式;
- 也就是我们使用6种基础模式能描绘一幅图像;
没有任何效果的卷积
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- 原像素中间像素值乘1;
- 其余像素全部乘以0;
- 像素值不会发生任何变化;
平划均值滤波
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
| 1/9 | 1/9 | 1/9 |
- 取九个值的平均值代替中间像素值;
- 可以起到平滑的效果;
高斯平滑
| 1/16 | 2/16 | 1/16 |
| 2/16 | 2/16 | 2/16 |
| 1/16 | 2/16 | 1/16 |
- 高斯平滑水平和垂直方向呈现高斯分布;
- 突出了中心点在像素平滑后的权重;
- 相较于均值滤波,有更好的平滑效果;
图像锐化
| -1 | -1 | -1 |
| -1 | 9 | -1 |
| -1 | -1 | -1 |
| 0 | -1 | 0 |
| -1 | 5 | -1 |
| 0 | -1 | 0 |
- 图像锐化使用拉普拉斯变换核函数;
边缘检测
,

- 使用
卷积上图;
- 会在图像中间黑白边界处获得比较大的值;
Sobel边缘检测
- 水平梯度卷积核
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
- 垂直梯度卷积核
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
- Sobel更强调和边缘相邻的像素点对边缘的影响;
卷积解决的问题
- 卷积负责提取图像中的局部特征
卷积--步长/stride
- 卷积核的尺寸
;
- 图片的尺寸
;
- 用卷积核来卷积图片;
- 每次移动一个像素;
- 输出结果的尺寸为:
;
- 如果每次移动不止一个像素,而是s个;
- 输出结果的尺寸为:
;
- s称为卷积步长/stride;
- 如果f或s的值比1大;
- 每次卷积之后结果的长宽,比卷积前小一些;
- 会丢失信息;
填充/padding
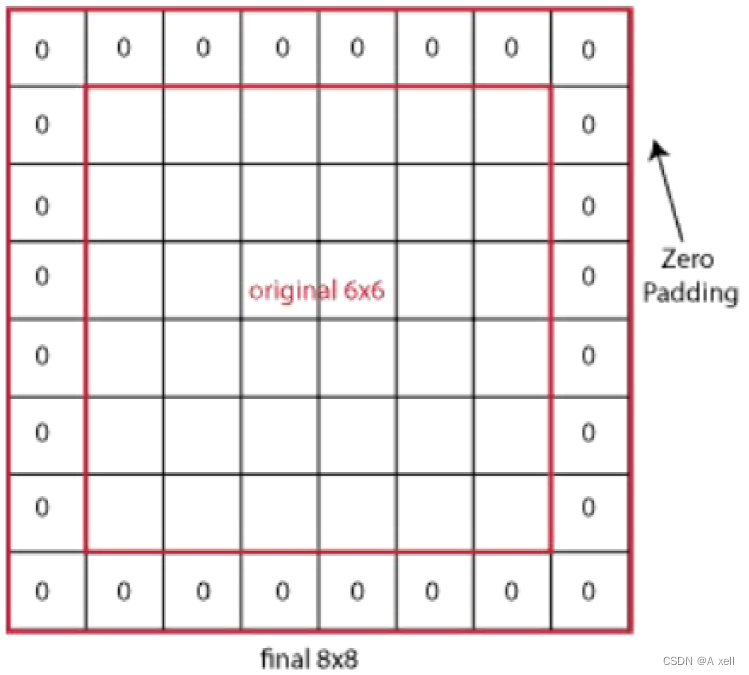
- 填充后,做卷积后的图像大小:
- 如果想让高(宽)不变:
- 假设步长s=1:
三种填充模式
- 橙色部分为图像/image;
- 蓝色部分为Filter/过滤器;
- 三种填充模式分别是full/same/valid;
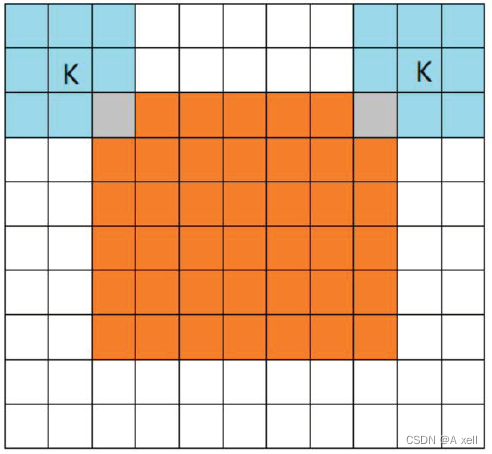
- 从filter和image刚相交开始做卷积.
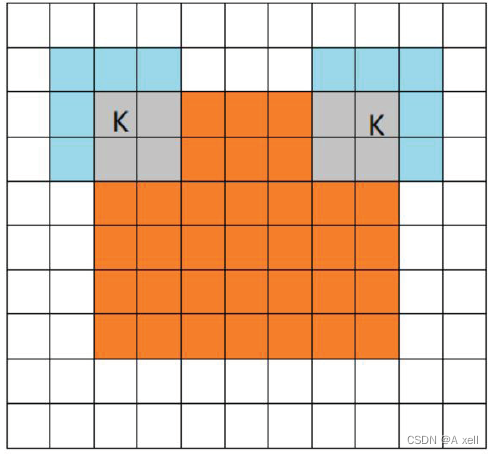
- filter中心(k)与image的边角重合,开始卷积;
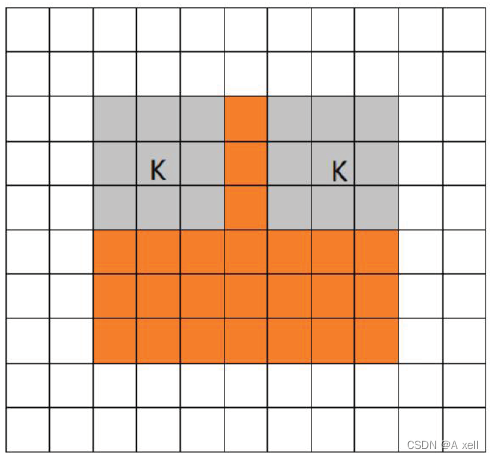
- filter全部在image内部时,开始卷积.
- same还有另外一个意思;
- 卷积后输出的feature map尺寸保持不变(相对于输入图片);
- same模式不代表完全输入输出尺寸一样;
- 同卷积核的步长有关系;
- same模式是最常见的模式;
- 该模式可以在卷积过程中保持图像大小不变;
三通道卷积
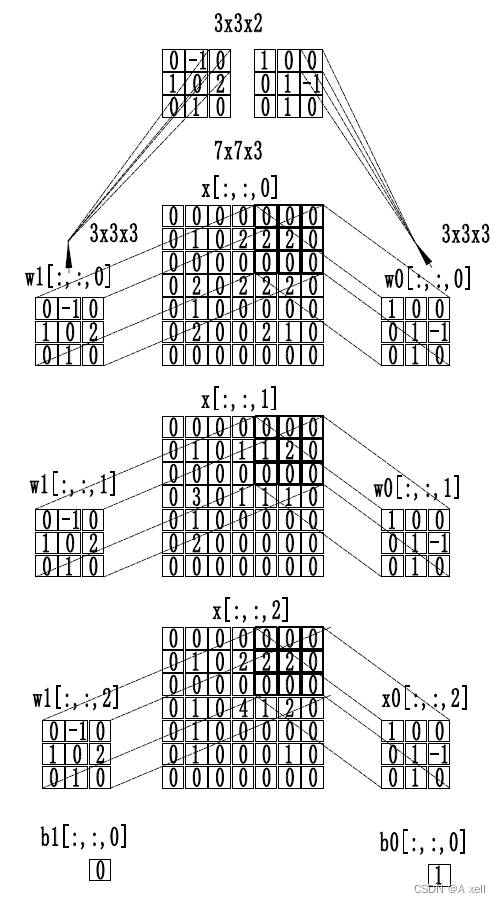
卷积核的确定
- CNN的厉害在于:
- 过滤器的特征不是人为设定;
- 而是通过大量图片自己训练出来的;