本篇文章参考:比较易懂的 Manacher(马拉车)算法配图详解
马拉车算法可以求出一个字符串中的最长回文子串,时间复杂度 O ( n ) O(n) O(n)
因为字符串长度的奇偶性,回文子串的中心可能是一个字符,也可能是两个字符中间的位置,所以为了解决这个问题,我们在每两个字符之间加一个 # ,开头再加一个 $ 防止越界
比如说:
abcd 变成 $#a#b#c#d#
接下来是后文需要的一些定义:
c表示当前已经计算过的最靠右的回文子串的中心点的下标m表示以 c 为中心的回文子串的右端点下标p[i]表示以s[i]为中心的回文子串的半径(包括自身)
对于以每一个位置为中心点的时候单独计算,复杂度很大,马拉车可以对其进行很好地优化
目前的难点就是怎么计算 p[i]

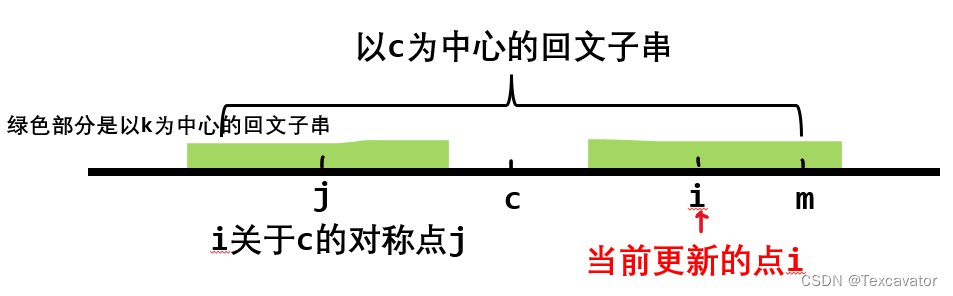
看上面这张图,我们当前需要计算 p[i],我们可以去找 i 关于 c 的对称点(记为 j),因为我们是从左往右计算的,所以 p[j] 已经计算过了,如果以 j 为中心的回文子串在以 c 为中心的回文子串中时,我们可以直接把 p[j] 赋给 p[i]
当然会出现一些特殊情况:
- 如果
p[j] + i > m,如下图所示,以 c 为中心的回文子串包不住,我们就更新p[i] = m - i(先只更新确定的部分)
- 如果 i 在 m 右侧,如下图所示,更新
p[i] = 1
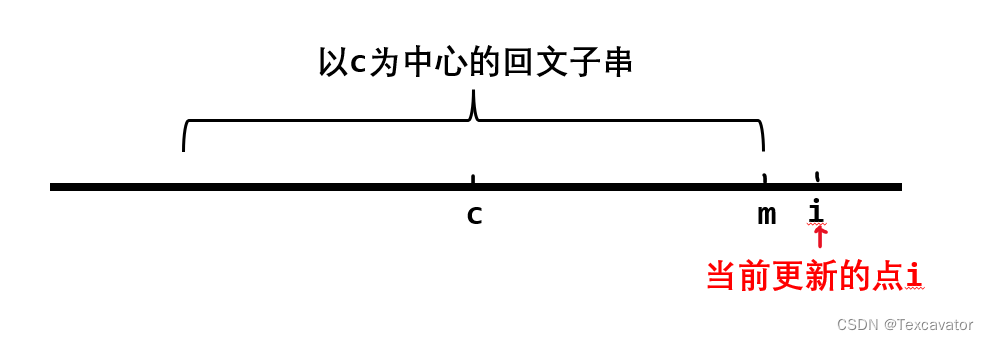
上面的情况都只能得到半成品的 p[i],所以需要对 s[i] 进行中心扩展,得到最终的 p[i]
如果最终的 p[i] + i > m 此时已经有比以 c 为中心的回文子串更靠右的回文子串了,就把 c = i m = p[i] + 1
求完 p[i] 后算法结束
求最长回文子串板子
string Manacher(string s)
{
int sl = s.size(); // 原字符串长度
if (sl == 0 || sl == 1) return s;
// 构建新串
string ns = "$#";
for (int i = 0; i < sl; i ++ )
{
ns += s[i];
ns += '#';
}
int len = ns.size();
int c = 0; // 最靠右的回文子串的中心点下标
int m = 0; // 最靠右的回文子串的右端点下标
int pos = 0; // 最长回文子串的中心点
int maxlen = 0; // 最长回文子串的半径(不包括中心点)(新字符串中)
vector<int> p(len); // p[i]表示以i为中心点的回文子串的半径(包括i)
for (int i = 1; i < len; i ++ )
{
if (i < m) p[i] = min(p[c - (i - c)], m - i + 1); // c-(i-c)是i关于c的对称点 当前情况表示i在目前最靠右侧的回文子串中
else p[i] = 1 + (ns[i] != '#'); // 当前不是#的话 其两侧就是# 所以半径可以加1
if (i - p[i] >= 0 && i + p[i] < ns.size())
while (ns[i - p[i]] == ns[i + p[i]]) p[i] ++ ; // 对半成品的i位置进行中心扩散
if (i + p[i] - 1 > m) // 产生了比以c为中心时更靠右的回文子串
{
c = i;
m = i + p[i] - 1;
}
if (p[i] - 1 > maxlen) // 更新最长回文子串
{
maxlen = p[i] - 1;
pos = i;
}
}
string ans = "";
char tmp;
for (int i = 0; i < 2 * maxlen * 1; i ++ ) // 遍历最长字串的每个位置 得出原字符串中的最长字串
{
tmp = ns[pos - (maxlen - 1) + i];
if (tmp != '#') ans += tmp;
}
return ans;
}
求最长前缀or后缀回文子串板子
string Manacher(string s)
{
int sl = s.size(); // 原字符串长度
if (sl == 0 || sl == 1) return s;
// 构建新串
string ns = "$#";
for (int i = 0; i < sl; i ++ )
{
ns += s[i];
ns += '#';
}
int len = ns.size();
int c = 0; // 最靠右的回文子串的中心点下标
int m = 0; // 最靠右的回文子串的右端点下标
int pos = 0; // 最长回文子串的中心点
int maxlen = 0; // 最长回文子串的半径(不包括中心点)(新字符串中)
// int flag; // 可以用这个标记是前缀回文子串最长还是后缀回文子串最长
vector<int> p(len); // p[i]表示以i为中心点的回文子串的半径(包括i)
for (int i = 1; i < len; i ++ )
{
if (i < m) p[i] = min(p[c - (i - c)], m - i + 1); // c-(i-c)是i关于c的对称点 当前情况表示i在目前最靠右侧的回文子串中
else p[i] = 1 + (ns[i] != '#'); // 当前不是#的话 其两侧就是# 所以半径可以加1
if (i - p[i] >= 0 && i + p[i] < ns.size())
while (ns[i - p[i]] == ns[i + p[i]]) p[i] ++ ; // 对半成品的i位置进行中心扩散
if (i + p[i] - 1 > m) // 产生了比以c为中心时更靠右的回文子串
{
c = i;
m = i + p[i] - 1;
}
if (p[i] == i && maxlen < p[i]) // 最长前缀回文子串
{
maxlen = p[i] - 1;
pos = i;
// flag = 1;
}
if (p[i] + i == len && maxlen < p[i]) // 最长后缀回文子串
{
maxlen = p[i] - 1;
pos = i;
// flag = 2;
}
}
string ans = "";
char tmp;
for (int i = 0; i < 2 * maxlen * 1; i ++ ) // 遍历最长字串的每个位置 得出原字符串中的最长字串
{
tmp = ns[pos - (maxlen - 1) + i];
if (tmp != '#') ans += tmp;
}
return ans;
}