粉刷房子

思路：

1.经验+题目要求

dp[i][0] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上红色，此时的最小花费。
dp[i][1] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上蓝色，此时的最小花费。
dp[i][2] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上绿色，此时的最小花费。

2.状态转移方程

因为相邻两个房子颜色不能相同，所以我们粉刷下一个位置只需要 找出上一个位置粉刷另外两种颜色最小花费即可。
比如： i 位置是红色，那么 i -1 只能是蓝和绿 ，找出min(dp[i-1][1] , dp[i-1][2]);

3.
有 i -1 ，建表多建一行/一列，要求最小花费，初始化为0即可不影响填表

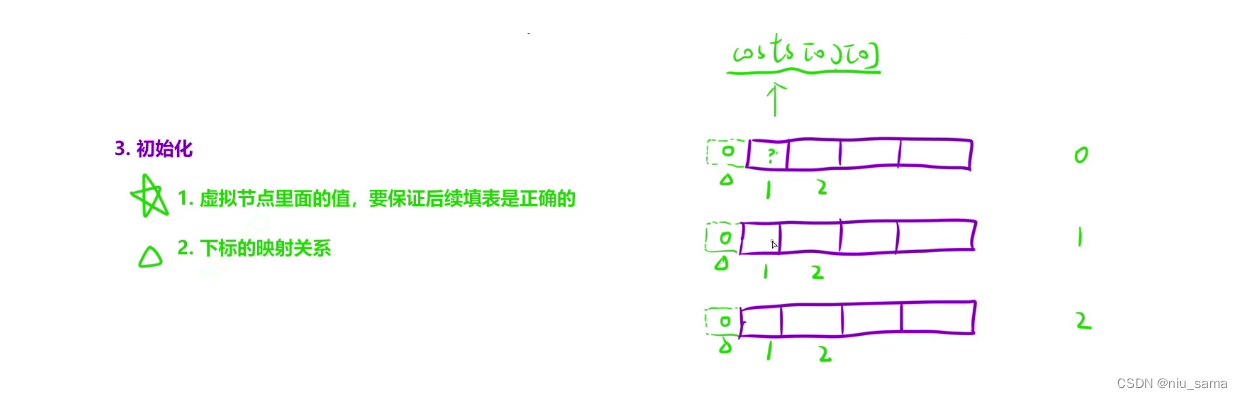
4 .
从左往右填表，一次填三个表

class Solution {
public:
    int minCost(vector<vector<int>>& costs) {
            int n = costs.size();
            vector<vector<int>> dp(n+1,vector<int>(3));
            for(int i = 1; i<=n; i++)
            {
                dp[i][0] = min(dp[i-1][1],dp[i-1][2]) +costs[i-1][0];
                dp[i][1] = min(dp[i-1][0],dp[i-1][2]) +costs[i-1][1];
                dp[i][2] = min(dp[i-1][0],dp[i-1][1]) +costs[i-1][2];
            }
            return min(min(dp[n][0],dp[n][1]),dp[n][2]);
    }
};

买卖股票的最佳时机含冷冻期

思路：

1.经验+题目要求

粉刷房子用颜色来表示的表，买卖股票可以用状态表示。

dp[i][0] 表示：第 i 天结束以后，处于" 买入 " 状态，此时的最大利润。
dp[i][1] 表示：第 i 天结束以后，处于" 可交易 " 状态，此时的最大利润。
dp[i][2] 表示：第 i 天结束以后，处于" 冷冻期 " 状态，此时的最大利润。

2.状态转移方程

每一个状态都可以由 另一个状态 转变成：买入 可以 从买入，可交易转换成。
例如： 买入 状态可以 当天啥也不干还是买入，也可以从可交易状态到买入，找出这两个状态的最大值即可。

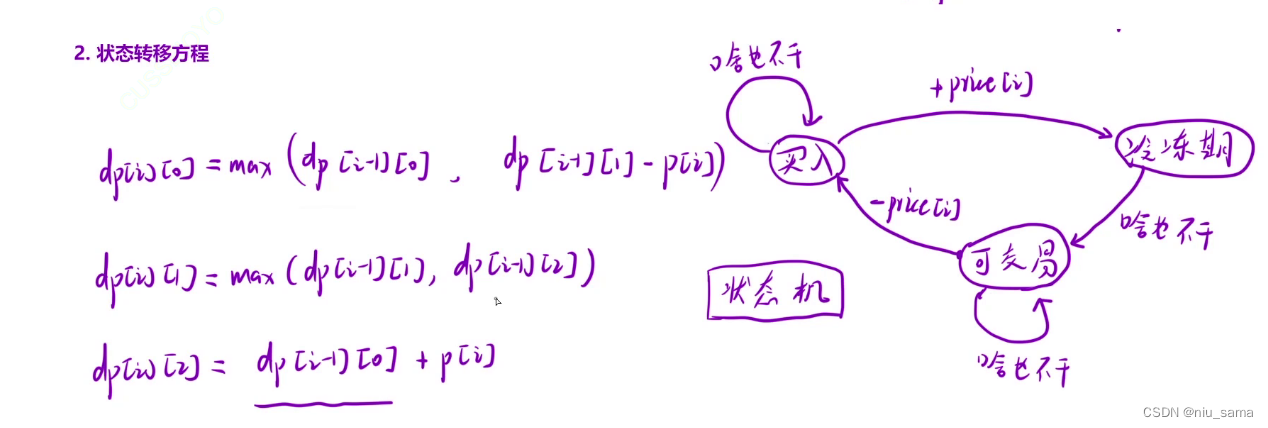
3. 初始化

只有买入状态的初始化，因为买入了所以为-p[0];

dp[0][0] = -p[0] , dp[0][1] = 0 , dp[0][2] = 0;

4.从左往右填写，一次填写三个表

class Solution {
public:
    int maxProfit(vector<int>& prices) {
         int n = prices.size();
         vector<vector<int>> dp(n+1,vector<int>(3));
         dp[0][0] = -prices[0];

         for(int i = 1; i<n; i++)
         {
             dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);
             dp[i][1] = max(dp[i-1][1],dp[i-1][2]);
             dp[i][2] = dp[i-1][0] + prices[i];
         }
        return max(max(dp[n-1][0],dp[n-1][1]),dp[n-1][2]);
    }
};

买卖股票的最佳时机含手续费

思路：

1.经验+题目要求

粉刷房子用颜色来表示的表，买卖股票可以用状态表示。

f[i] 表示：第 i 天结束之后，处于"买入" 状态，此时的最大利润
g[i] 表示：第 i 天结束之后，处于"卖出" 状态，此时的最大利润

注意手续费的位置，手续费的位置在从买入到卖出状态转换的位置上。

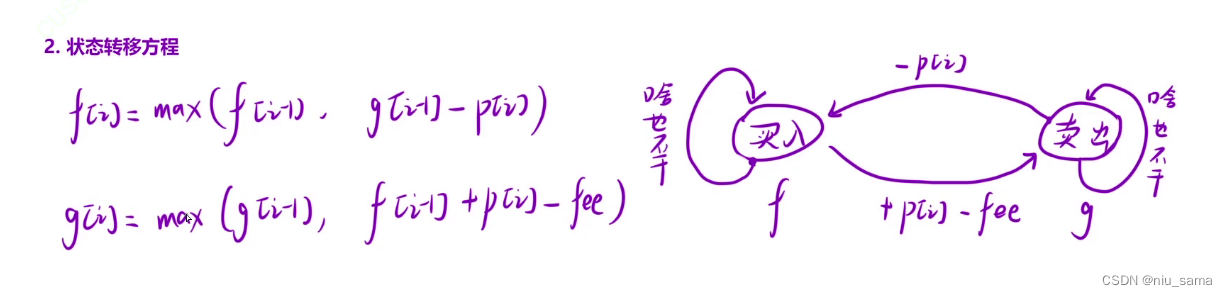
4.从左往右填写，两个表一起填

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<int> f(n);
        auto g = f;
        f[0] = -prices[0];

        for(int i = 1; i<n; i++)
        {
            f[i] = max(f[i-1],g[i-1]- prices[i] );
            g[i] = max(g[i-1],f[i-1] + prices[i] -fee);
        }

        return max(f[n-1],g[n-1]);
    }
};

买卖股票的最佳时机 III

思路：

1.经验+题目要求

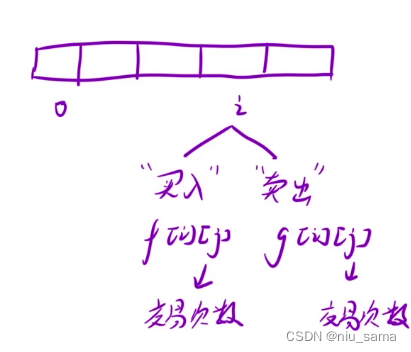
f[i][j] 表示：第 i 天结束之后，完成了 j 次交易，此时处于" 买入 " 状态下的最大利润
g[i][j] 表示：第 i 天结束之后，完成了 j 次交易，此时处于" 卖出 " 状态下的最大利润

状态之间的转换表达的状态转移方程和上面那几道题一样，但是，在判断 g[i][j] 的时候，需要注意j-1，j-1需要额外判断，
if(j-1) >=0 才能是 max状态转移方程，当j == 0时候，g[i][j] = g[i-1][j];

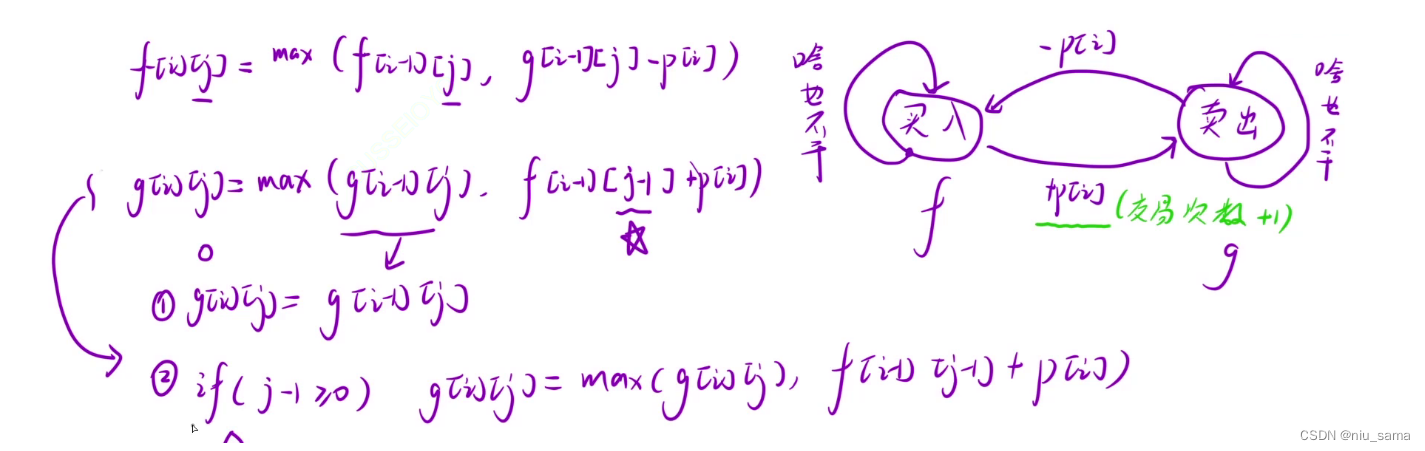
为了不影响max操作的比较，在第0天的时候，给第1和2次交易设为负无穷，但是又因为 上面 有g[i-1][j] - p[i] , 如果设为
INT_MIN ，就会超出范围，所以设为 -0x3f3f3f3f 。

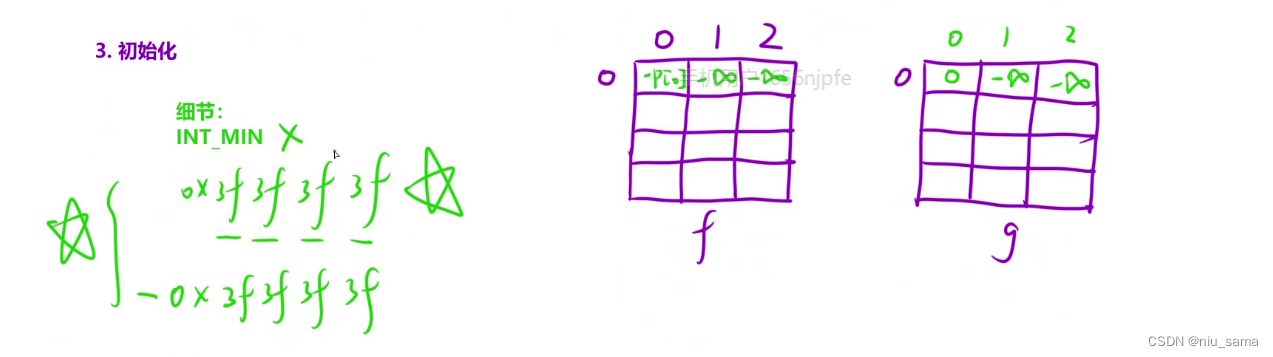
4.从上往下填写每一行，两个表一起填写。

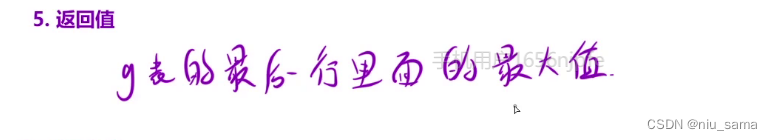
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n,vector<int>(3));
        auto g = f;
        //f表初始化
        f[0][0] = -prices[0];
        for(int i = 1; i<3; i++)
        {
            f[0][i] = -0x3f3f3f3f; //不能用INT_MIN,因为再+-都会超出极限
            g[0][i] = -0x3f3f3f3f;
        }

        //填表
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<3; j++)
            {
                f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
                if(j-1 >=0)
                    g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
                else
                    g[i][j] = g[i-1][j];
            }
        }

        int ret = 0;
        for(int i = 0; i<3; i++)
        {
            ret = max(ret,g[n-1][i]);
        }
        return ret;
    }
};

买卖股票的最佳时机 IV

同 买卖股票的最佳时机 III，就留给练习上一题了。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n,vector<int>(k+1));
        auto g = f;
        f[0][0] = -prices[0];
        for(int i = 1; i<k+1; i++)
        {
            f[0][i] = -0x3f3f3f3f;
            g[0][i] = -0x3f3f3f3f;
        }

        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<k+1; j++)
            {
                f[i][j] = max(f[i-1][j],g[i-1][j] -prices[i]);
                if(j-1 >= 0)
                    g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
                else
                    g[i][j] = g[i-1][j];
            }
        }

        int ret = 0;
        for(int i = 0; i<k+1; i++)
        {
            ret = max(ret,g[n-1][i]);
        }
        return ret;
    }
};