🐵本篇文章将对二叉树的相关概念、性质和遍历等知识进行讲解

---

  一、什么是树

在讲二叉树之前，先了解一下什么是树：树是一种非线性结构，其由许多节点和子节点组成，整体形状如一颗倒挂的树，比如下图：

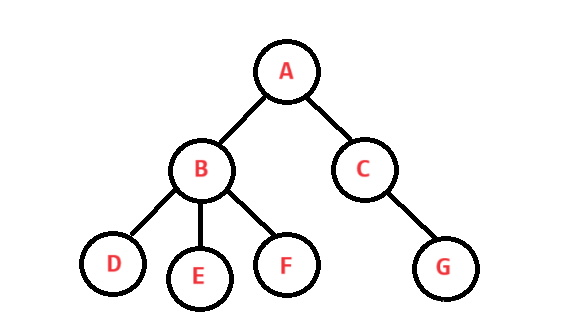
A就是这棵树的根，BDEF、D、CG、G等都可以看作这颗树的一颗子树，在树形结构中子树之间不能由交集，否则不能称为树，如下图就不是树：

二、树的相关概念

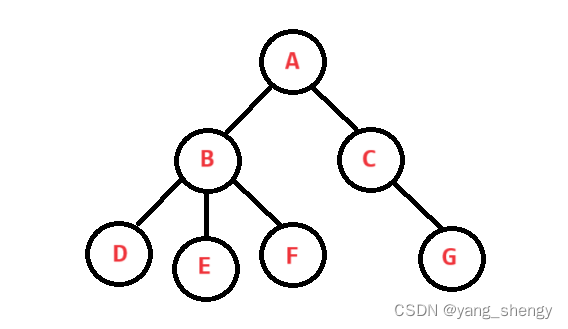
1. 结点的度：一个结点含有子结点的个数称为该结点的度，如A的度为2，B的度3，D的度为0

2. 树的度：所有结点度的最大值称为树的度，比如上树中B的度最大，则该树的度为3

3. 叶子结点/终端结点：度为0的结点称为叶子结点，如上树中的D E F G

4. 双亲结点/父结点：一个结点的前驱结点称为该结点的父结点，如B的父结点为A

5. 孩子结点/子结点：一个结点的后继结点称为该结点的子结点，如B的子结点有D E F

6. 根结点：没有双亲结点的结点称为根结点，上树的根结点为A

7. 结点的层次：从根结点那一层开始定义，A为第一层（有时是从0开始），B C所处第二层，依此类推

8. 树的高度：树中结点的最大层次为称为该树的高度，上树的高度为3

三、二叉树

二叉树是一种特殊的树，一棵所有结点的度都小于等于2的树称为二叉树

二叉树特别讲究顺序，如上图中如果G为C的左孩子，则又是一颗完全不同的二叉树

3.1 满二叉树

从根结点开始，从上到下从左到右每一层都放满了结点的树称为满二叉树，如下图：

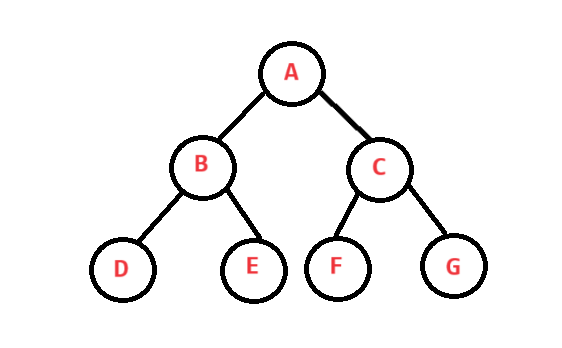
若一个满二叉树有k层，则其每一层有2^(k - 1)个结点，整个树共有(2^k) - 1个结点

3.2 完全二叉树

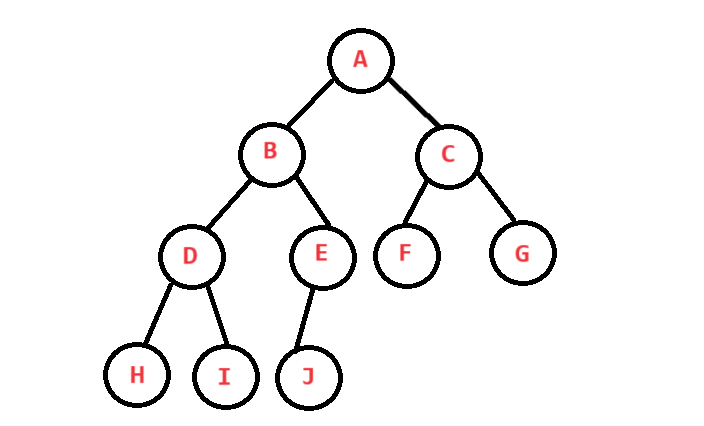
从根结点开始，从上到下从左到右依次存放结点，最后一层可以不满，这样的二叉树称为完全二叉树，如下图：

下图不是完全二叉树：

3.3 二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有2^(i - 1)个结点

2. 若规定根结点的层数为1，则一棵非空二叉树的最大结点数是(2^i) - 1

3. 对任何一棵二叉树，如果其叶结点个数为n0，度为2的结点个数为n2，则有n0＝n2＋1

4. 具有n个结点的完全二叉树的高度为：log₂(n + 1)向上取整，如：3.x为4；或者log₂(n) + 1向下取整，如3.x为3

5. 具有n个结点的完全二叉树，从上到下从左到右依次编号，规定根结点的编号为0，则编号为i的结点：双亲编号：(i - 1) / 2；左孩子编号：2i + 1，若2i + 1 > n则无左孩子；右孩子编号：2i + 2，若2i + 2 > n则无右孩子

下面讲一道例题：

一个具有767个节点的完全二叉树，其叶子节点个数为（）
A 383
B 384
C 385
D 386

【解析】由于二叉树中的结点的度都不大于2，所以设度为0，1，2的结点的个数分别为n0，n1，n2，则n0 + n1 + n2 = 767，由性质3：n0 = n2 + 1得2*n0 + n1 = 768，在完全二叉树中，度为1的结点只可能有1个或0个，如果n1 = 1，则n0不是一个整数，所以n1只可能为0，经计算n0 = 384

3.4 二叉树的存储

二叉树有两种存储方式，分别为链式存储和顺序存储，这里主要讲解链式存储，接下来用代码以穷举的方式先构造下面这个二叉树

public class BinaryTree {
    static class TreeNode{
        public char val; 
        public TreeNode left; //指向该结点的左孩子
        public TreeNode right; //指向该结点的右孩子

        public TreeNode(char val) {
            this.val = val;
        }
    }
}

接下来以穷举的方式构造二叉树

    public TreeNode creatTree() {
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');

        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        E.right = H;
        C.left = F;
        C.right = G;

        return A; //返回这个树的根结点
    }

3.5 二叉树的遍历

二叉树共有3种遍历方式，分别为：先序遍历、中序遍历、后序遍历，接下来会逐个讲解 

3.5.1 先序遍历

先序遍历一个树，按照根、左子树、右子树的顺序遍历这个树，直接看例子：

先遍历这个树的根A，之后遍历A的左B，由于B又是一个子树的根，所以要继续遍历B的左，B的左为空，那就遍历B的右：F，F是一个子树的根，所以要继续遍历F的左：D，D的左右都为空，那么F的左子树全部遍历完毕，接着遍历F的右，F的右为空，那么B的右全部遍历完毕，那接着就是A的左全部遍历完毕，之后遍历A的右：C，C又是一个子树的根，所以要继续遍历C的左，C的左为空，那就遍历C的右：G，G的左右都为空，至此A的右也全部遍历完毕，那么整个二叉树遍历完毕整个遍历的序列为：A B F D C G

3.5.2 中序遍历

先序遍历一个树，按照左子树、根、右子树的顺序遍历这个树，直接看例子：

先遍历A的左，由于A的左也是一个子树，所以要遍历这个子树的左：空，这个子树的左遍历完就要遍历这个树的根：B，之后遍历这个子树的右：F D，这也是一个子树，所以要先遍历这个子树左：D，然后遍历根：F，最后是右，右为空，那么整个二叉树的左遍历完毕，接着遍历根：A，然后遍历右子树：C G，先遍历这个树的左，左为空，然后遍历根：C，最后是右：G，至此整个二叉树遍历完毕，整个遍历的序列为：B D F A C G

3.5.3 后序遍历

先序遍历一个树，按照左子树、右子树、根的顺序遍历这个树，直接看例子：

先遍历这个二叉树的左子树：B F D，这也是一个树，所以先遍历这个树的左，左为空，然后遍历这个树的右子树：F D，这也是一个树，所以要先遍历这个树的左：D，然后遍历这个树的右，右为空，最后是根：F，那么B F D这个子树的右遍历完毕，然后遍历B F D这个树的根：B，至此整个树的左子树遍历完毕，然后遍历这个树的右子树：C G，先遍历这个树的左，左为空，然后遍历右：G，再遍历根C，最后遍历整个树的根：A，整个树遍历完毕，整个遍历的序列为：D F B G C A

3.6 代码实现二叉树的遍历

二叉树的三种遍历需要用递归的思想实现

先序遍历：

    public void preOrder(TreeNode root) {
        if (root == null) { //如果根为空则直接返回
            return;
        }

        System.out.print(root.val +" ");
        preOrder(root.left); //以根的左孩子为新的根继续遍历
        preOrder(root.right); //以根的右孩子为新的根继续遍历
    }

root为null后返回至上一个方法，遍历D的右孩子，右孩子也为空，则以D为根的方法结束返回至上一个方法，遍历B的右孩子

右子树也是同样的道理

中序遍历：

    public void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }

        preOrder(root.left);
        System.out.print(root.val +" ");
        preOrder(root.right);
    }

后序遍历：

    public void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }

        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.val +" ");
    }