详解动态规划（算法村第十九关青铜挑战）

news2024/9/27 23:24:17

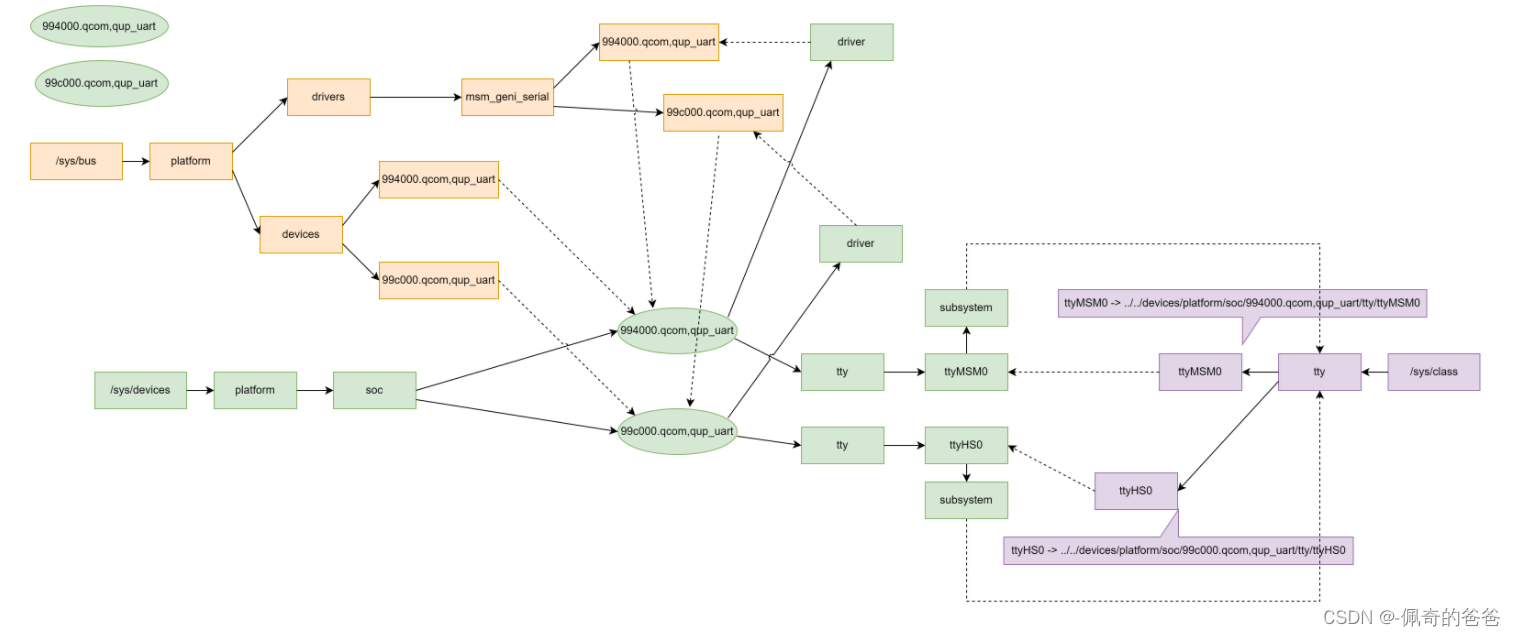
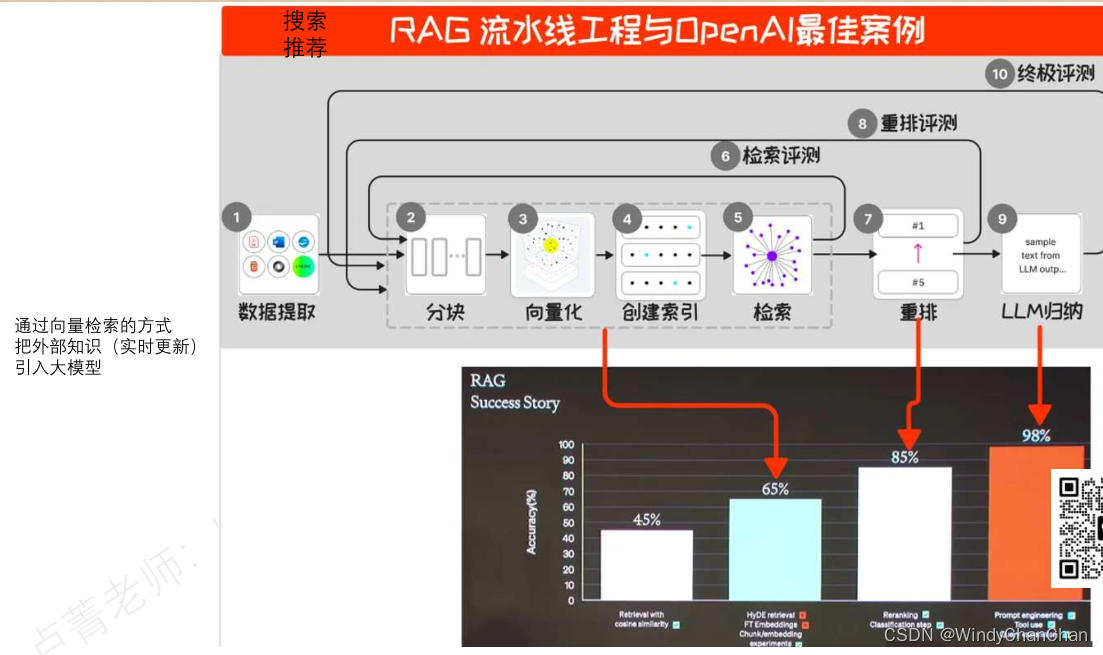
不同路径

62. 不同路径 - 力扣（LeetCode）

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

递归

递归的含义就是处理方法不变，但是问题的规模减少。

public int uniquePaths(int m, int n)
{
    //如果只剩一行或者一列，那只有一个方向，一条路径了
    if (m == 1 || n == 1)
        return 1;

    //往右走一步，问题规模缩小成 m * (n-1) 的网格
    //往下走一步，问题规模缩小成 (m-1) * n 的网格
    return uniquePaths(m, n - 1) + uniquePaths(m - 1, n);
}

但在此题中普通的递归解法超时，原因是存在大量重复计算。

在这里插入图片描述

例如，不管是从(0,1)还是(1,0)从来到（1,1），接下来从（1,1）到终点都会有2种走法，不必每次都重新计算。而普通的递归只能一遍又一遍地计算从（1,1）到终点有多少种走法。

利用二维数组进行记忆化搜索

在这里插入图片描述

每个格子的数字表示从起点开始到达当前位置的路径数，计算总路径时可以先查一下记录，如果有记录就直接读，没有再计算，这样就可以避免大量重复计算，这就是记忆化搜索。

第一行和第一列都是1。
其他格子的值 = 左侧格子的值 + 上方格子格子的值。

如图中的4，由上面的1和左侧的3计算而来，15由上侧的5和左侧的10计算而来。

public int uniquePaths_2(int m, int n)
{
    int[][] record = new int[m][n];
    record[0][0] = 1;

    for (int row = 0; row < m; ++row)
        for (int col = 0; col < n; ++col)
        {
            if (row > 0 && col > 0)
                record[row][col] = record[row - 1][col] + record[row][col - 1];
            else if (col > 0)	//第一行格子
                record[row][col] = record[row][col - 1];
            else if(row > 0)	//第一列格子
                record[row][col] = record[row - 1][col];
        }

    return record[m - 1][n - 1];
}

将二维数组优化为一维数组

第一步，用1填充一维数组。

在这里插入图片描述

第二步，从头遍历数组，除了第一个位置，位置的新值 = 前一个位置的值 + 位置的原始值。其实，在二维数组中，位置的原始值就在位置新值的上方。

在这里插入图片描述

重复第二步

在这里插入图片描述

把三个一维数组拼接起来，发现恰好跟上面的二维数组一致：

在这里插入图片描述

所以，路径总数就是一维数组最后一个元素的值。

这种反复更新的一维数组就是滚动数组。

public int uniquePaths_3(int m, int n)
{
    int[] dp = new int[n];
    Arrays.fill(dp,1);

    for (int row = 1; row < m; row++)
        for (int col = 1; col < n; col++)
                dp[col] = dp[col - 1] + dp[col];

    return dp[n - 1];
}

总结

这个题目涵盖了dp的多个方面，比如重复子问题（递归）、记忆化搜索（将已经计算好的结果存入数组，后面用到就直接读取）、滚动数组（二维数组优化为一维数组）。

最小路径和

64. 最小路径和 - 力扣（LeetCode）

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步

解

public int minPathSum(int[][] grid)
{
    //逐行遍历，更新 grid 的格值，作为[在方向约束下，从起点到当前格的最小路经和]
    for (int row = 0; row < grid.length; row++)
        for (int col = 0; col < grid[row].length; col++)
        {
            if (row == 0 && col == 0)
                continue;
            else if (row == 0)  //只能往右走
                grid[row][col] = grid[row][col - 1] + grid[row][col];
            else if (col == 0)  //只能往下走
                grid[row][col] = grid[row - 1][col] + grid[row][col];
            else                //从[往右、往下]两个方向挑路径和最小的走
                grid[row][col] = Math.min(grid[row][col - 1], grid[row - 1][col]) + grid[row][col];
        }

    return grid[grid.length - 1][grid[0].length - 1];
}

在这里插入图片描述

我们完全不需要建立 dp 矩阵浪费额外空间，直接遍历 grid 并修改其值即可。因为原 grid 矩阵元素中被覆盖为 dp 元素后（都处于当前遍历点的左上方），不会再被使用到。

三角形最小路径和

120. 三角形最小路径和 - 力扣（LeetCode）

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是下标与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即 2 + 3 + 5 + 1 = 11）。

自底向上 dp + 空间优化

public int minimumTotal(List<List<Integer>> triangle)
{
    int[] dp = new int[triangle.size() + 1];  //多出一格是为了dp数组能够获取triangle最底层的值

    // 从最底层开始 dp
    for (int row = triangle.size() - 1; row >= 0; row--)
        for (int col = 0; col < row + 1; col++) //第 row 行有 row + 1个数
            dp[col] = Math.min(dp[col], dp[col + 1]) + triangle.get(row).get(col);

    //顶点储存着从最底层到顶点的最小路径和
    return dp[0];
}