AtCoder Beginner Contest 284 A - E

news2024/10/5 21:13:50

题目地址：AtCoder Beginner Contest 284 - AtCoder

一个不知名大学生，江湖人称菜狗
original author: jacky Li
Email : 3435673055@qq.com

Time of completion：2023.1.8
Last edited: 2023.1.8

目录

题目地址：AtCoder Beginner Contest 284 - AtCoder

AtCoder Beginner Contest 284 A - E

A - Sequence of Strings

思路

参考代码

B - Multi Test Cases 

思路

参考代码

C - Count Connected Components

思路

参考代码

D - Happy New Year 2023 

思路

参考代码

E - Count Simple Paths

思路

参考代码

AtCoder Beginner Contest 284 A - E

A - Sequence of Strings

思路

建立一个字符串数组，依次读入，倒序输出就好。

参考代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <cstring>
#include <unordered_map>
#include <unordered_set>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
#define IOS std::ios::sync_with_stdio(false)
#define inf 0x3f3f3f3f
#define YES cout << "YES" << endl
#define NO cout << "NO" << endl
#define int long long
#define x first
#define y second
//#define cmp [&](PII a, PII b){ return a.y < b.y; }

const int N = 5e5+10, mod = 1e9+7, M = 1e6+5, K = 1e5+10, Z = 2e5+7;

using namespace std;
typedef long long LL;
typedef priority_queue<int> PQI; 
typedef priority_queue <int, vector<int>, greater<>> PQGI;
typedef pair<int, int> PII;

string a[12]; 

void solve()
{
	int n; cin >> n;
	for(int i = 1; i <= n; i ++) cin >> a[i];
	for(int i = n; i >= 1; i --) cout << a[i] << endl;
	return;
}

signed main()
{
    IOS; cin.tie(0); cout.tie(0);
    int T = 1;
//    cin >> T;
    while( T -- ) solve();
    return 0;
}

B - Multi Test Cases 

思路

T组用例，用一个odd变量来数奇数个数，逐个输入逐个输出

参考代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <cstring>
#include <unordered_map>
#include <unordered_set>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
#define IOS std::ios::sync_with_stdio(false)
#define inf 0x3f3f3f3f
#define YES cout << "YES" << endl
#define NO cout << "NO" << endl
#define int long long
#define x first
#define y second
//#define cmp [&](PII a, PII b){ return a.y < b.y; }

const int N = 5e5+10, mod = 1e9+7, M = 1e6+5, K = 1e5+10, Z = 2e5+7;

using namespace std;
typedef long long LL;
typedef priority_queue<int> PQI; 
typedef priority_queue <int, vector<int>, greater<>> PQGI;
typedef pair<int, int> PII;

void solve()
{
	int n, odd = 0; cin >> n;
	for(int i = 1; i <= n; i ++)
	{
		int a; cin >> a;
		if(a & 1) odd ++;
	}
	cout << odd << endl;
}

signed main()
{
    IOS; cin.tie(0); cout.tie(0);
    int T = 1;
    cin >> T;
    while( T -- ) solve();
    return 0;
}

C - Count Connected Components

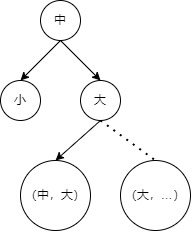
思路

该题的输入：

5 3
1 2
1 3
4 5
输出：

2

该题是让查找连通块的个数，上面样例如下图所示。

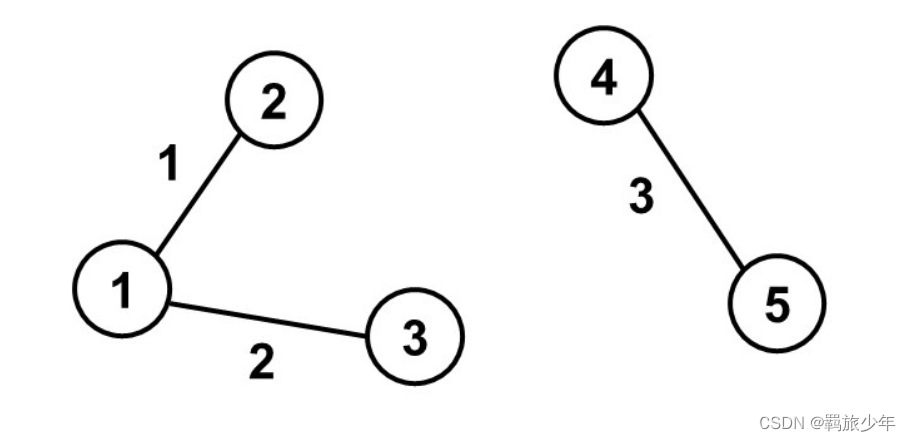
 所以运用并查集的板子可以直接求解

参考代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <cstring>
#include <unordered_map>
#include <unordered_set>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
#define IOS std::ios::sync_with_stdio(false)
#define inf 0x3f3f3f3f
#define YES cout << "YES" << endl
#define NO cout << "NO" << endl
#define int long long
#define x first
#define y second
//#define cmp [&](PII a, PII b){ return a.y < b.y; }

const int N = 5e5+10, mod = 1e9+7, M = 1e6+5, K = 2e5+10, Z = 1e5+7;

using namespace std;
typedef long long LL;
typedef priority_queue<int> PQI; 
typedef priority_queue <int, vector<int>, greater<>> PQGI;
typedef pair<int, int> PII;

int p[K], st[K], ans;

void init()
{
	for(int i = 1; i <= K - 5; i ++) p[i] = i;
}

int find(int x)
{
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
}

void solve()
{
	init();
	int n, m; cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int a, b; cin >> a >> b;
		p[find(b)] = find(a);
	}
	
	for(int i = 1; i <= n; i ++)
		st[find(i)] = true;
	
	for(int i = 1; i <= n; i ++)
		if(st[i] == true) ans ++;
	cout << ans << endl;
}

signed main()
{
    IOS; cin.tie(0); cout.tie(0);
    int T = 1;
//    cin >> T;
    while( T -- ) solve();
    return 0;
}

D - Happy New Year 2023 

思路

该题让寻找q^2 * p = n，而n的范围达到了9e18的大小，

由数学知识可得，p 和 q一定有一个值得范围小于9e18的三次跟即3e6，

而且题目中说明有唯一解，而且一定有解使题目变得简单许多，只需要对p、q同时判断，便可以

参考代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <cstring>
#include <unordered_map>
#include <unordered_set>

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#define IOS std::ios::sync_with_stdio(false)
#define inf 0x3f3f3f3f
#define YES cout << "YES" << endl
#define NO cout << "NO" << endl
#define int long long
#define x first
#define y second
//#define cmp [&](PII a, PII b){ return a.y < b.y; }

const int N = 5e5+10, mod = 1e9+7, M = 5e7+5, K = 2e5+10, Z = 1e5+7, X = 1.5 * 1e9;

using namespace std;
typedef long long LL;
typedef priority_queue<int> PQI; 
typedef priority_queue <int, vector<int>, greater<>> PQGI;
typedef pair<int, int> PII;

int primes[M], cnt;
bool st[M];

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

void solve()
{
	// 题目中说给的用例一定有解，且唯一解，使题目难度降低，因为读错题目写了两种 
	int n; cin >> n;
	for(int i = 0; i < cnt; i ++)
	{
		int t = primes[i];
		if(n % t == 0) 
		{
			n = n / t;
			if(n % t == 0)
			{
				int a = t, b = n / t;
				cout << a << ' '  << b << endl;
				break;
			}
			else 
			{
				int a = sqrt(n), b = t; // 题目中给说了有唯一确定的值，前面没看见唯一确定的值。 
				cout << a << ' ' << b << endl;
				break;
			}
		}
	}
//	int t = pow(n, 0.333333333333333333);
//	int s = lower_bound(primes + 1, primes + cnt + 1, t) - (primes + 1);
//	for(int i = s; i <= cnt; i ++)
//	{
//		if(n % (primes[i] * primes[i]) == 0)
//			{cout << primes[i] << ' ' << (n / (primes[i] * primes[i])) << endl; break;}
//	}
	return;
}

signed main()
{
    IOS; cin.tie(0); cout.tie(0);
    get_primes(3e6);
    int T = 1;
    cin >> T;
    while( T -- ) solve();
    return 0;
}

E - Count Simple Paths

思路

dfs搜索，超过1e6的时候跳出，由于是递归不能使用return结束。要使用exit(0);

参考代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <cstring>
#include <unordered_map>
#include <unordered_set>

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#define IOS std::ios::sync_with_stdio(false)
#define inf 0x3f3f3f3f
#define YES cout << "YES" << endl
#define NO cout << "NO" << endl
#define int long long
#define x first
#define y second
#define cmp [&](PII a, PII b){ return a.y < b.y; }

const int N = 5e5+10, mod = 1e9+7, M = 5e7+5, K = 2e5+10, Z = 1e5+7, X = 1.5 * 1e9;

using namespace std;
typedef long long LL;
typedef priority_queue<int> PQI; 
typedef priority_queue <int, vector<int>, greater<>> PQGI;
typedef pair<int, int> PII;

vector<vector<int>> adj(K);
vector<int> vis(K);
int ans;
int df = 0;

void dfs(int df, int x)
{
    if(vis[x]) return;
    ans ++;
    if(ans == 1000000)
    {
        cout << ans << endl;
        exit(0);
    }
    vis[x] = 1;
    for(auto y : adj[x])
    {
        dfs(df, y);
    }
    vis[x] = 0;
}

void solve()
{
    int n, m; cin >> n >> m;
    for(int i = 1; i <= m; i ++)
    {
        int u, v; cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

//  auto dfs = [&](auto dfs, int x)
//  {
//      if(vis[x]) return;
//      ans ++;
//      if(ans == 1000000)
//      {
//          cout << ans << endl;
//          exit(0);
//      }
//      vis[x] = 1;
//      for(auto y : adj[x])
//      {
//          dfs(dfs, y);
//      }
//      vis[x] = 0;
//  };
    dfs(df, 1);
    cout << ans << endl;
}

signed main()
{
    IOS; int T = 1;
    cin.tie(nullptr); 
    cout.tie(nullptr);
//    cin >> T;
    while( T -- ) solve();
    return 0;
}

作者有言

如果感觉博主讲的对您有用，请点个关注支持一下吧，将会对此类问题持续更新……

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/148616.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于FPGA的UDP 通信（一）

基于FPGA的UDP 通信（一）

引言手头的FPGA开发板上有一个千兆网口&#xff0c;最近准备做一下以太网通信的内容。本文先介绍基本的理论知识。FPGA芯片型号&#xff1a;xc7a35tfgg484-2网口芯片&#xff08;PHY&#xff09;&#xff1a;RTL8211网络接口&#xff1a;RJ45简述以太网什么以太网&#xff1f;以…
阅读更多...
k8s之实战小栗子

k8s之实战小栗子

写在前面 本文一起看一个基于k8s的实战小栗子&#xff0c;在这篇文章 中我们基于docker搭建了一个WordPress网站。本文就通过k8s再来实现一遍。架构图如下&#xff1a; ![在这里插入图片描述](https://img-blog.csdnimg.cn/9c73ac0c183a429a8f4b1a2feb363527.png 从上图可以…
阅读更多...
使用Origin计算数据的上升\下降时间

使用Origin计算数据的上升\下降时间

使用Origin计算上升/下降时间计算上升时间1导入数据&#xff0c;做图2、选择合适的数据范围3、选择上升时间和上升范围两个测量参数&#xff0c;获得结果4、更改区间&#xff0c;并导出数据计算下降时间1、将感兴趣区域移动到下降沿2、更改为测量下降沿参数获得结果上升时间小工…
阅读更多...
【Kotlin】空安全 ④ ( 手动空安全管理 | 空合并操作符 ?: | 空合并操作符与 let 函数结合使用 )

【Kotlin】空安全 ④ ( 手动空安全管理 | 空合并操作符 ?: | 空合并操作符与 let 函数结合使用 )

文章目录一、空合并操作符 ?:二、空合并操作符与 let 函数结合使用一、空合并操作符 ?: 空合并操作符 ?: 用法 : 表达式 A ?: 表达式 B如果 表达式 A 的值 不为 null , 则 整个表达式的值 就是 表达式 A 的值 ; 如果 表达式 A 的值 为 null , 则 整个表达式的值 就是 表达…
阅读更多...
vue-路由的使用方式

vue-路由的使用方式

1.下载路由 使用npm的下载: # vue2对应版本 npm i vue-router3# vue3对应版本 npm i vue-router42.路由初试化 路由的三种模式: history, 指定路由的模式, 有hash,history,memory三种模式,一般使用第一种和第三种模式 createWebHashHistory hash模式 > http://localhost…
阅读更多...
十大字符串函数与内存操作函数

十大字符串函数与内存操作函数

前言&#xff1a;我们知道在C语言的库中有许许多多的库函数&#xff0c;今天我就来介绍一下自己对两大类库函数中一些常用函数的认识和理解&#xff0c;希望对大家有帮助。 说明&#xff1a;下文中会花较大篇幅实现这些库函数的模拟&#xff0c;请大家不要觉得库函数直接用就好…
阅读更多...
UNet入门总结

UNet入门总结

作者&#xff1a;AI浩 来源&#xff1a;投稿 编辑&#xff1a;学姐 Unet已经是非常老的分割模型了&#xff0c;是2015年《U-Net: Convolutional Networks for Biomedical Image Segmentation》提出的模型。 论文连接&#xff1a;https://arxiv.org/abs/1505.04597 在Unet之前…
阅读更多...
Android 深入系统完全讲解（4）

Android 深入系统完全讲解（4）

4 SystemServer 创建过程 SystemServer 进程非常关键了&#xff0c;我们上层的服务都是在这里以线程的形式存在&#xff0c;比如 AMS&#xff0c;PMS&#xff0c;WindowManagerService&#xff0c;壁纸服务&#xff0c;而关于调试这个服务进程&#xff0c;我们随后就会讲到。 …
阅读更多...
虚拟人-面部表情-Audio2Face语音驱动表情

虚拟人-面部表情-Audio2Face语音驱动表情

任务&#xff1a; 输入自己的音频&#xff0c;导入maya模型&#xff0c;让maya模型通过音频驱动说话 教程&#xff1a; https://www.bilibili.com/video/BV1rZ4y1R7H4/?p2&spm_id_frompageDriver&vd_sourceef114f70c3fd4d5394f12dbd3d022bbe 一.下载和安装 1.首先…
阅读更多...
Java面试常见问题-SE篇

Java面试常见问题-SE篇

JavaSE面试问题汇总①int和Integer的区别为什么设计封装类型&#xff1f;JDK、JRE、JVM的区别和equals方法的区别hashCode()与equals()之间的关系泛型中extends和super的区别String、StringBuffer、StringBuilder的区别重载和重写的区别接口和抽象类的区别List与Set的区别Array…
阅读更多...
2023/1/8总结

2023/1/8总结

今天学了了强连通算法 Tarjan算法 Tarjan算法是一种求解有向图强连通分量的线性时间的算法&#xff0c;他运用到了DFS算法以及DFS的特性和数据结构——栈。 算法介绍&#xff1a;如果两个顶点可以相互通达&#xff0c;则称两个顶点强连通(strongly connected)。如果有向图G…
阅读更多...
LeetCode题解 二叉树（十三）：701 二叉搜索树的插入操作；450 删除二叉搜索树中的结点

LeetCode题解 二叉树（十三）：701 二叉搜索树的插入操作；450 删除二叉搜索树中的结点

701 二叉搜索树的插入操作 medium 给定二叉搜索树&#xff08;BST&#xff09;的根节点和要插入树中的值&#xff0c;将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证&#xff0c;新值和原始二叉搜索树中的任意节点值都不同。 如果要按照题目中所说改变二叉…
阅读更多...
渗透测试中的常用编码

渗透测试中的常用编码

渗透测试中的常用编码 页面编码 在网页设置网页编码 在中加入设置特定html标签 这样页面的编码就会变成utf-8 &#xff0c;如果没有设置编码就会使用默认 的编码&#xff0c;而浏览器默认编码与之不同就会出现乱码。 常用的有三种格式分别是 utf-8、gbk、gbk2312 ascii编码…
阅读更多...
_Linux 进程信号-信号处理篇

_Linux 进程信号-信号处理篇

文章目录前言捕捉信号1. 内核如何实现信号的捕捉2. sigaction代码验证可重入函数volatile(关键字)SIGCHLD信号实验一实验二前言 信号发送 信号处理 已经讲过&#xff0c;本章讲解信号处理最后一部分。 捕捉信号 信号捕捉过程图 经过信号捕捉过程图&#xff1a;我们知道信号…
阅读更多...
语音文件分析

语音文件分析

语音文件格式的重要参数 语音波形，它的这个文件，主要的格式就是采样率，那么电话或者嵌入式设备，采样率一般是8000Hz，就一秒钟8000个点，如果是PC机麦克风，那是16K，就一秒钟是16000个点，像这个CD是高保真的，音乐唱片的是用这个44.1K。 量化位数，又叫采样精度，…
阅读更多...
绿通科技在创业板通过注册：收入依赖美国市场，张志江为实控人

绿通科技在创业板通过注册：收入依赖美国市场，张志江为实控人

2023年1月6日&#xff0c;证监会发布关于同意广东绿通新能源电动车科技股份有限公司&#xff08;下称“绿通科技”或“绿通电动车”&#xff09;、杭州国泰环保科技股份有限公司首次公开发行股票注册的批复。换句话说&#xff0c;证监会同意上述两家公司的创业板IPO注册。 同日…
阅读更多...
【手写 Vue2.x 源码】第十一篇 - Vue 的数据渲染流程

【手写 Vue2.x 源码】第十一篇 - Vue 的数据渲染流程

一&#xff0c;前言 上篇&#xff0c;主要介绍了数组数据变化的观测情况&#xff0c;涉及以下几个点&#xff1a; 实现了数组数据变化被劫持后&#xff0c;已重写原型方法的具体逻辑&#xff1b;数组各种数据变化时的观测情况分析&#xff1b; 目前为止&#xff0c;数据劫持…
阅读更多...
webpack 如何编写 loader

webpack 如何编写 loader

三种本地开发测试 loader 的方法 1. 匹配&#xff08;test&#xff09;单个 loader 你可以通过在 rule 对象使用 path.resolve 指定一个本地文件&#xff1a; webpack.config.js const path require(path);module.exports {//...module: {rules: [{test: /\.js$/,use: [{…
阅读更多...
Ansible Automation Platform - 在 RHEL 安装 Ansible Automation Platform 2.3 环境

Ansible Automation Platform - 在 RHEL 安装 Ansible Automation Platform 2.3 环境

《OpenShift / RHEL / DevSecOps 汇总目录》 文本已在 RHEL 9 AAP 2.3 环境中进行验证。 说明&#xff1a; 本文介绍如何在一个节点上部署一套 all-in-one 的 Ansible Automation Platform 2.3 的运行环境。红帽 Ansible Automation Platform 2.3 需要至少 RHEL 8.4 以上的环…
阅读更多...
【EHub_tx1_tx2_E100】Ubuntu18.04 + ROS_ Melodic + Velodyne VLP-16雷达 测试使用

【EHub_tx1_tx2_E100】Ubuntu18.04 + ROS_ Melodic + Velodyne VLP-16雷达 测试使用

简介&#xff1a;介绍 Velodyne VLP-16 16线激光雷达 在EHub_tx1_tx2_E100载板&#xff0c;TX1核心模块环境&#xff08;Ubuntu18.04&#xff09;下测试ROS驱动&#xff0c;打开使用RVIZ 查看点云数据&#xff0c;本文的前提条件是你的TX1里已经安装了ROS版本&#xff1a;Melod…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023